バイナリツリーの奇数レベルを反転する-PHPチュートリアル-php.cn

2415。二分木の奇数レベルを反転

難易度: 中

トピック: ツリー、深さ優先検索、幅優先検索、バイナリツリー

完璧なバイナリツリーのルートが与えられた場合、ツリーの各奇数レベルでノード値を反転します。

たとえば、レベル 3 のノード値が [2,1,3,4,7,11,29,18] であるとすると、[18,29,11,7,4,3,1] になるはずです。 ,2].

反転したツリーのルートを返します。

すべての親ノードに 2 つの子があり、すべてのリーフが同じレベルにある場合、バイナリツリーは完璧です。

ノードのレベルは、ノードとルートノード間のパスに沿ったエッジの数です。

例 1:

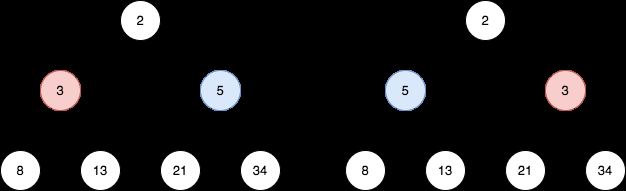
Reverse Odd Levels of Binary Tree

入力: root = [2,3,5,8,13,21,34]
出力: [2,5,3,8,13,21,34]
説明:
- ツリーには奇数レベルが 1 つだけあります。
- レベル 1 のノードはそれぞれ 3、5 ですが、反転して 5、3 になります。

例 2:

Reverse Odd Levels of Binary Tree

入力: root = [7,13,11]
出力: [7,11,13]
説明:
- レベル 1 のノードは 13、11 ですが、これを反転すると 11、13 になります。

例 3:

入力: root = [0,1,2,0,0,0,0,1,1,1,1,2,2,2,2]
出力: [0,2,1,0,0,0,0,2,2,2,2,1,1,1,1]
説明:
- 奇数レベルにはゼロ以外の値があります。
- レベル 1 のノードは 1、2 であり、反転後は 2、1 です。
- レベル 3 のノードは 1、1、1、1、2、2、2、2 で、反転後は 2、2、2、2、1、1、1、1 です。

制約:

ツリー内のノードの数は [1, 2¹⁴] の範囲内です。
0 5
ルートは完全な二分木です。

ヒント:

レベルごとに独立して再帰的に解決してみてください。
深さ優先検索の実行中に、左右のノード (ペアにする必要があります) を次のレベルに渡します。現在のレベルが奇数の場合は、その値を反転するか、そうでない場合は再帰的に次のレベルに移動します。

解決策:

バイナリツリーに対して深さ優先トラバーサルを実行する必要があります。タスクは、奇数レベルのノード値を反転することです。完全な二分木とは、すべての非リーフノードに 2 つの子があり、すべてのリーフノードが同じレベルにあることを意味します。

DFS (深さ優先検索) アプローチを使用し、奇数レベルごとにノード値を反転します。以下はこれを実現するソリューションです。

重要なポイント:

ツリーは完璧です。つまり、完全にバランスが取れており、すべてのリーフノードが同じレベルにあります。
奇数レベルのノードのみを反転する必要があります。奇数のレベルは、レベル 1 から始まるインデックスが付けられます (1 位、3 位、5 位など)。
DFS を使用すると、ツリーを走査し、ノードのレベルを識別できます。奇数のレベルに遭遇した場合、そのレベルのノードの値を交換します。
各レベルで、左の子と右の子という 2 つの子ノードをトラバースします。

アプローチ：

ツリーの深さ優先の走査を実行します。
現在のレベルのノードの各ペアについて:
- レベルが奇数の場合、ノード値を交換します。
現在のノードの左右の子を再帰的に処理し、更新されたレベル情報を渡します。
ツリー全体を処理した後、ルートノードを返します。

プラン：

ルートノードから開始します。
再帰関数 dfs を使用してツリーをトラバースし、奇数レベルでノード値を反転します。
現在のレベルを追跡して、奇数のレベルを特定します。
奇数レベルで値を交換し、子の DFS 走査を続行します。
処理後にルートを返します。

解決策の手順:

再帰関数 dfs($left, $right, $isOddLevel) を定義します。
- left: 左の子ノード。
- right: 右側の子ノード。
- isOddLevel: 現在のレベルが奇数かどうかを示すブール値。
左が null かどうかを確認します。存在する場合は、これ以上処理するノードがないため、戻ります。
isOddLevel が true の場合、左右のノードの値を交換します。
次の場合に dfs 関数を再帰的に呼び出します。
- 左の子と右の子 (次のレベル)。
- 右は左の子、左は右の子 (次のレベル)。
dfs($root->left, $root->right, true) で再帰を開始し、ルートを返します。

このソリューションを PHP で実装してみましょう: 2415。二分木の奇数レベルを反転

<?php
class TreeNode {
    public $val = 0;
    public $left = null;
    public $right = null;

    public function __construct($val = 0, $left = null, $right = null) {
        $this->val = $val;
        $this->left = $left;
        $this->right = $right;
    }
}

class Solution {
    /**
     * @param TreeNode $root
     * @return TreeNode
     */
    public function reverseOddLevels($root) {
       ...
       ...
       ...
       /**
        * go to ./solution.php
        */
    }

    /**
     * Helper function to perform DFS
     *
     * @param $left
     * @param $right
     * @param $isOddLevel
     * @return void
     */
    private function dfs($left, $right, $isOddLevel) {
       ...
       ...
       ...
       /**
        * go to ./solution.php
        */
    }
}

// Example usage:
$root = new TreeNode(2);
$root->left = new TreeNode(3);
$root->right = new TreeNode(5);
$root->left->left = new TreeNode(8);
$root->left->right = new TreeNode(13);
$root->right->left = new TreeNode(21);
$root->right->right = new TreeNode(34);

$solution = new Solution();
$reversedRoot = $solution->reverseOddLevels($root);

// Function to print the tree for testing
function printTree($root) {
    if ($root === null) {
        return;
    }
    echo $root->val . " ";
    printTree($root->left);
    printTree($root->right);
}

printTree($reversedRoot); // Output: 2 5 3 8 13 21 34
?>

ログイン後にコピー

説明：

TreeNode Class: 値 (val) と 2 つの子 (左、右) を持つバイナリツリーノードの構造を表します。
reverseOddLevels 関数: ルートノードの左右の子で DFS を開始し、レベル 1 (奇数レベル) から開始します。
dfs 関数:
- 2 つのノード (左右) とブール値 isOddLevel を取得して、現在のレベルが奇数かどうかを判断します。
- 現在のレベルが奇数の場合、左右の値が入れ替わります。
- isOddLevel 値を交互に繰り返しながら、次のレベルに対して自分自身を再帰的に呼び出します (true が false、またはその逆)。
再帰は各レベルの次のノードのペアの処理に進み、奇数レベルのノードのみが反転されるようにします。

チュートリアルの例:

例 1:

入力:

ログイン後にコピー

レベル 0: [2] (偶数、変化なし)。
レベル 1: [3, 5] (奇数、[5, 3] の逆)。
レベル 2: [8、13、21、34] (偶数、変化なし)。

出力:

ログイン後にコピー

例 2:

入力:

       7
      / \
     13  11

ログイン後にコピー

レベル 0: [7] (偶数、変化なし)。
レベル 1: [13, 11] (奇数、[11, 13] の逆)。

出力:

       7
      / \
     11  13

ログイン後にコピー

時間計算量:

時間計算量: O(n)、n はバイナリツリー内のノードの数です。深さ優先の方法で各ノードに 1 回だけアクセスします。
空間複雑度: O(h)、h は木の高さです。再帰の深さはツリーの高さに対応し、最悪の場合 (歪んだツリーの場合) は O(n) になりますが、完全な二分木の場合は O(log n) になります。

このソリューションは、時間計算量 O(n) の深さ優先探索を使用して、完全なバイナリツリーの奇数レベルにあるノードを効率的に反転します。このコードは奇数レベルで値を交換し、再帰的アプローチを使用してツリーを処理します。

連絡先リンク

このシリーズが役立つと思われた場合は、GitHub で リポジトリ にスターを付けるか、お気に入りのソーシャルネットワークで投稿を共有することを検討してください。あなたのサポートは私にとって大きな意味を持ちます!

このような役立つコンテンツがさらに必要な場合は、お気軽にフォローしてください: