JavaScript画像処理 - アフィン変換の深い理解_JavaScriptスキル
前の記事 では、画像ピラミッドについて説明しました。この記事では、アフィン変換について学びます。
アフィン?
任意のアフィン変換は、行列 (線形変化) とベクトル (並進変化) に変換、乗算できます。
実際、アフィンは 2 つの画像間の変換関係です。
たとえば、アフィン変換を通じて画像に対してスケーリング、回転、平行移動などの操作を実行できます。
数学の問題
アフィン問題を解く前に、数学の問題を解いてみましょう。
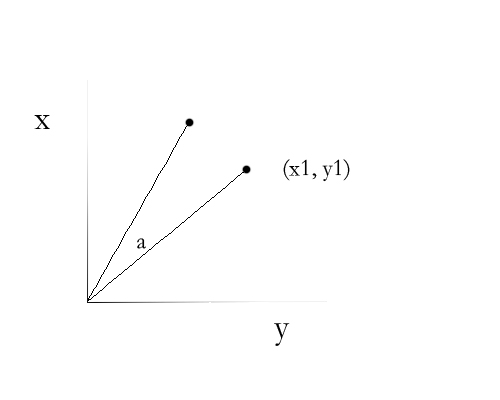
図のように、点(x1,y1)は原点に対して角度aだけ回転しますが、この点はどこに行くのでしょうか?
座標系を極座標系に変更すると、点 (x1, y1) は (r, β) になり、回転すると (r, α β) になります。
デカルト座標系に戻ると、回転した点は (cos(α β) * r, sin(α β) * r) になります。
次に、式 を使用します:
cos(α β)=cosαcosβ-sinαsinβ
sin(α β)=sinαcosβ cosαsinβ
であり、元の点は (cosβ * r, sinβ * r) であるため、新しい点を (x1 * cosα - y1 * sinα, x1 *) として取得するのは簡単です。 sinaα y1 *cosα)。
そこから回転変換式 を導き出すことができます:
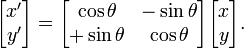
この場合、変換は比較的単純で、ベクトル (c, d) を追加するのと同じです。
変換行列関数の実装を取得します
通常、アフィン変換を表すには 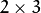 行列を使用します。
行列を使用します。
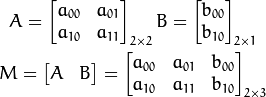
ここで、A は回転スケーリング変換、B は平行移動変換です。この場合、結果 T は次の条件を満たします:
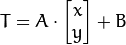 または
または
![T = M cdot [x, y, 1]^{T}](http://files.jb51.net/file_images/article/201301/201301160852597.png)
つまり: 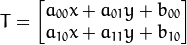
var getRotationArray2D = function (__angle, __x, __y){
var sin = Math.sin(__angle) || 0,
cos = Math.cos(__angle) ||
x = __x | | 0,
y = __y ||
return [cos, -sin, -x,
sin, cos, -y
]; >
このようにして、アフィン変換行列を取得します。
もちろん、原点が左上隅に固定されているため、この実装自体にはいくつかの問題があります。 アフィン変換の実装
var height = __src.row,
width = __src.col,
dst = __dst || new Mat(height, width, CV_RGBA),
sData = new Uint32Array(__src.buffer)、
dData = new Uint32Array(dst.buffer);
var i, j, xs, ys, x, y, nowPix; >for (j = 0, nowPix = 0; j < height; j ){
xs = __rotArray[1] * j __rotArray[2]
ys = __rotArray[4] * j __rotArray[5] ;
for(i = 0; i
if(xs > 0 && ys > 0 && xs < 幅 && ys < 高さ){
x = xs 0; x] ;
}else{
dData[nowPix] = 4278190080 //黒
}
}
} else{
error(arguments.callee, UNSPPORT_DATA_TYPE; /* {line} */);
}
戻り値
};
この関数はまず行列データを 32 ビット形式に変換し、各要素を操作することは各ピクセルを操作することに相当します。
次に、すべての要素を走査し、対応する点に値を割り当てます。
効果


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7396
7396
 15
15
 1630
1630
 14
14
 1358
1358
 52
52
 1268
1268
 25
25
 1217
1217
 29
29
 画像処理タスクでワッサーシュタイン距離はどのように使用されますか?
Jan 23, 2024 am 10:39 AM
画像処理タスクでワッサーシュタイン距離はどのように使用されますか?
Jan 23, 2024 am 10:39 AM
EarthMover's Distance (EMD) としても知られるワッサーシュタイン距離は、2 つの確率分布間の差を測定するために使用される指標です。従来の KL 発散または JS 発散と比較して、Wasserstein 距離は分布間の構造情報を考慮に入れるため、多くの画像処理タスクで優れたパフォーマンスを示します。 Wasserstein 距離は、2 つのディストリビューション間の最小輸送コストを計算することにより、あるディストリビューションを別のディストリビューションに変換するために必要な最小作業量を測定できます。このメトリクスは、分布間の幾何学的差異を捉えることができるため、画像生成やスタイル転送などのタスクで重要な役割を果たします。したがって、ワッサーシュタイン距離が概念になります
 ビジョントランスフォーマー(VIT)モデルの動作原理と特性の詳細な分析
Jan 23, 2024 am 08:30 AM
ビジョントランスフォーマー(VIT)モデルの動作原理と特性の詳細な分析
Jan 23, 2024 am 08:30 AM
VisionTransformer (VIT) は、Google が提案した Transformer ベースの画像分類モデルです。従来の CNN モデルとは異なり、VIT は画像をシーケンスとして表し、画像のクラス ラベルを予測することで画像の構造を学習します。これを実現するために、VIT は入力イメージを複数のパッチに分割し、チャネルを通じて各パッチのピクセルを連結し、線形投影を実行して目的の入力寸法を実現します。最後に、各パッチが単一のベクトルに平坦化され、入力シーケンスが形成されます。 Transformer のセルフ アテンション メカニズムを通じて、VIT は異なるパッチ間の関係を捕捉し、効果的な特徴抽出と分類予測を実行できます。このシリアル化された画像表現は、
 AI テクノロジーを使用して古い写真を復元する方法 (例とコード分析付き)
Jan 24, 2024 pm 09:57 PM
AI テクノロジーを使用して古い写真を復元する方法 (例とコード分析付き)
Jan 24, 2024 pm 09:57 PM
古い写真の修復は、人工知能テクノロジーを使用して古い写真を修復、強化、改善する方法です。このテクノロジーは、コンピューター ビジョンと機械学習アルゴリズムを使用して、古い写真の損傷や欠陥を自動的に特定して修復し、写真をより鮮明に、より自然に、より現実的に見せることができます。古い写真の復元の技術原則には、主に次の側面が含まれます: 1. 画像のノイズ除去と強化 古い写真を復元する場合、最初にノイズ除去と強化を行う必要があります。平均値フィルタリング、ガウス フィルタリング、バイラテラル フィルタリングなどの画像処理アルゴリズムとフィルタを使用して、ノイズやカラー スポットの問題を解決し、写真の品質を向上させることができます。 2. 画像の修復と修復 古い写真には、傷、ひび割れ、色あせなどの欠陥や損傷がある場合があります。これらの問題は、画像の復元および修復アルゴリズムによって解決できます。
 画像超解像再構成におけるAI技術の応用
Jan 23, 2024 am 08:06 AM
画像超解像再構成におけるAI技術の応用
Jan 23, 2024 am 08:06 AM
超解像度画像再構成は、畳み込みニューラル ネットワーク (CNN) や敵対的生成ネットワーク (GAN) などの深層学習技術を使用して、低解像度画像から高解像度画像を生成するプロセスです。この方法の目的は、低解像度の画像を高解像度の画像に変換することで、画像の品質と詳細を向上させることです。この技術は、医療画像、監視カメラ、衛星画像など、さまざまな分野で幅広く応用されています。超解像度画像再構成により、より鮮明で詳細な画像を取得できるため、画像内のターゲットや特徴をより正確に分析および識別することができます。再構成方法 超解像度画像の再構成方法は、一般に、補間ベースの方法と深層学習ベースの方法の 2 つのカテゴリに分類できます。 1) 補間による手法 補間による超解像画像再構成
 Java 開発: 画像認識と処理を実装する方法
Sep 21, 2023 am 08:39 AM
Java 開発: 画像認識と処理を実装する方法
Sep 21, 2023 am 08:39 AM
Java 開発: 画像認識と処理の実践ガイド 要約: コンピューター ビジョンと人工知能の急速な発展に伴い、画像認識と画像処理はさまざまな分野で重要な役割を果たしています。この記事では、Java 言語を使用して画像認識と処理を実装する方法と、具体的なコード例を紹介します。 1. 画像認識の基本原理 画像認識とは、コンピューター技術を使用して画像を分析および理解し、画像内のオブジェクト、特徴、またはコンテンツを識別することを指します。画像認識を実行する前に、図に示すように、いくつかの基本的な画像処理技術を理解する必要があります。
 PHP学習メモ:顔認識と画像処理
Oct 08, 2023 am 11:33 AM
PHP学習メモ:顔認識と画像処理
Oct 08, 2023 am 11:33 AM
PHP 学習メモ: 顔認識と画像処理 はじめに: 人工知能技術の発展に伴い、顔認識と画像処理が話題になっています。実際のアプリケーションでは、顔認識と画像処理は主にセキュリティ監視、顔ロック解除、カード比較などに使用されます。一般的に使用されるサーバー側スクリプト言語として、PHP を使用して顔認識や画像処理に関連する機能を実装することもできます。この記事では、具体的なコード例を使用して、PHP での顔認識と画像処理について説明します。 1. PHP における顔認識 顔認識は
 C# 開発における画像処理とグラフィカル インターフェイスの設計の問題に対処する方法
Oct 08, 2023 pm 07:06 PM
C# 開発における画像処理とグラフィカル インターフェイスの設計の問題に対処する方法
Oct 08, 2023 pm 07:06 PM
C# 開発における画像処理とグラフィカル インターフェイス設計の問題に対処する方法には、特定のコード サンプルが必要です はじめに: 最新のソフトウェア開発では、画像処理とグラフィカル インターフェイス設計は一般的な要件です。 C# は汎用の高水準プログラミング言語として、強力な画像処理機能とグラフィカル インターフェイス設計機能を備えています。この記事は C# に基づいており、画像処理とグラフィカル インターフェイスの設計の問題に対処する方法について説明し、詳細なコード例を示します。 1. 画像処理の問題: 画像の読み取りと表示: C# では、画像の読み取りと表示は基本的な操作です。使用できます。N
 スケール不変特徴量 (SIFT) アルゴリズム
Jan 22, 2024 pm 05:09 PM
スケール不変特徴量 (SIFT) アルゴリズム
Jan 22, 2024 pm 05:09 PM
スケール不変特徴変換 (SIFT) アルゴリズムは、画像処理およびコンピューター ビジョンの分野で使用される特徴抽出アルゴリズムです。このアルゴリズムは、コンピュータ ビジョン システムにおけるオブジェクト認識とマッチングのパフォーマンスを向上させるために 1999 年に提案されました。 SIFT アルゴリズムは堅牢かつ正確であり、画像認識、3 次元再構成、ターゲット検出、ビデオ追跡などの分野で広く使用されています。複数のスケール空間内のキーポイントを検出し、キーポイントの周囲の局所特徴記述子を抽出することにより、スケール不変性を実現します。 SIFT アルゴリズムの主なステップには、スケール空間の構築、キー ポイントの検出、キー ポイントの位置決め、方向の割り当て、および特徴記述子の生成が含まれます。これらのステップを通じて、SIFT アルゴリズムは堅牢でユニークな特徴を抽出することができ、それによって効率的な画像処理を実現します。




