Three.js ソースコードの読み方メモ(基本コア Core オブジェクト)_基礎知識
Three.js は、ブラウザーの 3D プログラミングを簡素化し、JavaScript を使用してブラウザーで複雑なシーンを簡単に作成できる優れた WebGL オープン ソース ライブラリです。 Github 上にたくさんの webgl デモがあるので、私は興奮して試してみたいと思っています。このライブラリはまだ開発段階にあるため、情報が非常に少なく、愛好家はほとんどの場合、ライブラリのソース コードを読んで学ぶ必要があり、現在そうするつもりです。
これは、最も基本的な Core オブジェクトから始まる最初のメモです。
Core::Vector2
このコンストラクターは、2 次元ベクトルを表すオブジェクトを作成するために使用されます
THREE.Vector2 = function ( x, y ) {
this.x = x || 0; = y || 0;
};
コードをコピー
this.y = y;
return this;
copy: function ( v ) {
this.x = v.x;
this.y = v.y;
},
... // その他の関数
関数 set(x, y) はベクトルの値を指定するために使用され、呼び出し元自身の x、y 値が影響を受け、メソッド自体が呼び出し元に戻ります。この状況は非常に一般的です。以下では説明しません。テキストによって機能を明確に表現できる関数は、ソース コードを参照しなくなりますが、これについては以下では説明しません。
関数 copy(v) は、ベクトル v を呼び出し元にコピーするために使用されます。
関数 add(a,b) と関数 sub(a,b) は、それぞれベクトル a とベクトル b の加算と減算を表します。
関数 addSelf(v) と subSelf(v) はそれぞれ、ベクトル v を呼び出し元自体に加算または減算することを意味します。
関数 multiplyScale(s) と diveScale(s) は、それぞれ呼び出し元を s で乗算または除算することを表します。
関数 lerpSelf(v,alpha) は、呼び出し元を v が指す方向にアルファだけ回転させます。アルファが 1 の場合、呼び出し元は最終的に v に等しくなります。アルファ = 0 の場合、呼び出し元は依然として元の値と等しくなります。 。
コードをコピー
コードは次のとおりです。
関数 distanceToSquared(v) と distanceTo(v) は、呼び出し元とベクトル v の間の距離を返します。ここでの距離は、実際には 2 つのベクトルの始点が原点にあるときの終点間の距離であり、ベクトル this-v の長さになります。
関数 setLength(s) は、方向を変更せずにベクトルの長さを s にスケールします。
関数equals(v)は、呼び出し元の値とベクトルvが同じかどうかを判断します。
関数 isZero() は、呼び出し元がゼロ ベクトルであるかどうかを判断します。
関数 clone() は、呼び出し元と同じ値を持つ新しいベクトルを返します。これは、copy(v) との違いに注意してください。
このコンストラクターは、3 次元ベクトルを表すオブジェクトを作成します
コードをコピー
コードは次のとおりです。
THREE.Vector3 = function ( x, y, z ) {
this.x = x || 0; y || 0 ;
3 次元ベクトルと 2 次元ベクトルには、set、add、dot、length、clone など、多くの共通点があります。ここではすべて省略し、3 次元ベクトルが持つ機能の一部のみを説明します。 2次元ベクトルよりも記録されます。
関数 setX(x)、setY(y)、setZ(z) は、特定のコンポーネントの値を個別に設定するために使用されます。
関数cross(a,b)とcrossSelf(v)はそれぞれ、呼び出し元をa、bの外積、または呼び出し元自体とvの外積にします。外積は、外積に関与する 2 つのベクトルに垂直なベクトルであり、右螺旋の法則に従います。
関数 getPositionFromMatrix(m)、getRotationFromMatrix(m)、getScaleFromMatrix(m) は、4×4 モデル行列から位置成分、回転成分、スケーリング成分を抽出します。モデル行列は、一連の平行移動、回転、およびスケーリング変換の重ね合わせ効果を表します。 (ここの 2 番目の関数はドキュメントに記載されていますが、ソース コードでは他の 2 つの関数に置き換えられています。おそらくまだ更新されていないでしょう)。
関数 angleTo(v) は、呼び出し元とベクトル v の間の角度を計算します。
Core::Vector4
このコンストラクターは、4 次元ベクトルを表すオブジェクトを作成します
THREE.Vector4 = function (x, y, z, w) {
this.x = x || 0; y = y ||
this.w = (w !== 未定義);
🎜>4 次元ベクトル 同次座標を表すために使用され、その機能は Vector2 および Vector3 の機能と重複します。コンポーネントが 1 つだけ多いため、ここでは記録しません。
Core::Matrix3
このコンストラクターは、3×3 行列を表すオブジェクトを作成します
THREE.Matrix3 = function () { this.elements = new Float32Array(9 ) ; };
3×3 行列には 9 つの要素があり、行列要素の elements 属性に格納されます。
関数 getInverse(m) は、呼び出し元自体を変更しながら、行列 m の逆行列を返します。
関数 transpose() は呼び出し元を転置します。
関数 transposeToArray(r) は、それ自体を変更せずに呼び出し元を配列 r に転置します。 (この場所のソース コードが間違っているようです。var m=this.m は var m=this.elements である必要があります。)
Core::Matrix4
このコンストラクターは 4x を作成します4 マトリックス オブジェクト、4×4 マトリックスは、3 次元グラフィックスにおいて非常に重要です。モデル マトリックス、ビュー マトリックス、投影マトリックスはすべてこのようなマトリックスです。
コードをコピー
n32 || 0、(n33 !== 未定義) || | 0, n43 || 0, ( n44 !== unknown ) ? n44 : 1
};
Matrix3 オブジェクトに含まれるいくつかの関数Matrix4 では関数もここでは省略されています。
関数identity()は、オブジェクトを単位行列にリセットします。
関数 lookAt(eye, center, up) はオブジェクトをビュー行列として設定し、パラメーターはすべて Vector3 オブジェクトです。この行列は目と中心の相対位置のみを使用します。このビュー行列は、カメラが目の位置から中心位置に向かっており、上向きベクトル(後述)が上であるときのビュー行列を表している。ビュー行列はカメラのモデル行列とみなすことができるため、この関数によって生成された行列は次の変換を表すことができます。オブジェクトを原点から中心の目の位置まで平行移動し、上向きベクトルが上になるまで回転します。 。上向きベクトルはカメラを固定するために使用されます。カメラが 1 点に固定され、レンズが固定方向を向いている場合でも、上向きベクトルはカメラのこの寸法を固定します。 。
コードをコピー
コードは次のとおりです:
x .cross( up, z ).normalize();
if ( x.length() === 0 ) {
z.x = 0.0001;
x.cross( up, z ) .normalize() ;
}
te[0] = x.x; te[8] = z.x; 1] = x.y ; te[9] = z.y; te[6] = y.z;
🎜>}、
関数 multiply(a,b)、multiplySelf(v)、および multiplyToArray(a,b,r) は 2 つの行列を乗算します。
関数 multiplyScale(s) は、オブジェクトの 16 要素すべてに s を乗算します。
関数 multiplyVector3(v) および multiplyVector4(v) は、オブジェクト行列に 4 次元行ベクトルを左乗算し、vector3 および Vector4 タイプの行ベクトルを返します。オブジェクト行列がモデル ビュー行列で、入力ベクトルが点の位置情報である場合、出力ベクトルはモデル変換とカメラ変換後のカメラに対する点の位置になります。 Vector3 型のベクトルを入力すると同次座標に自動的に補完され、返されると第 4 成分が切り取られて通常の座標になります。
関数rotateAxis(v)は、オブジェクト行列の左上隅にある3×3の部分行列を使用して行ベクトルvを左乗算し、新しい行ベクトルを取得して正規化し、この新しい行ベクトルを返します。行ベクトル。この関数はベクトル v の値も更新します。モデル ビュー マトリックスの左上隅にある 3×3 サブマトリックスには、モデル マトリックスの回転情報が含まれています。このサブマトリックスを左にベクトルで乗算すると、取得された新しいベクトルが実際には回転後の元のベクトルになります (回転効果)。のモデル行列から来ています)。したがって、この関数はrotateAxisと呼ばれます。
rotateAxis: function ( v ) {
var te = this.elements;
var vx = v.x, vy = v.y, vz = v.z;
v.x = vx * te[0] vy * te[4] vz * te[8]; >v.y = vx * te[1] vy * te[5] vz * te[9];
v.z = vx * te[2] vy * te[6] vz * te[10]; .normalize( );
return v;
},
関数crossVector(v)は、行列オブジェクト(呼び出し元)とvの外積を計算します。オブジェクト行列と 4 次元行ベクトル v を乗算すると、ベクトルが返されます。これは具体的に何をするのか、まだ分かりません。
var v = new THREE.Vector4();
v.x = te[0] * a.x te[4] * a.y te[8] * a.z te[12] * a.w ;
v.y = te[1] * a.x te[5] * a.y te[9] * a.z te[13] * a.w;
v.z = te[2] * a.x te[6] * a.y te[ 10] * a.z te[14] * a.w;
v.w = ( a.w ) te[3] * a.x te[7] * a.y te[11] * a.z te[15] * a.w : 1; v を返します。
}、
関数 determinant() は行列の行列値を計算します。
関数 flattenToArray( flat) と関数 flattenToArrayOfset( flat,offset) は、行列を 1 次元配列にダンプします。前者の関数は flat[0] から flat[15] までを格納します。後者の関数は、ストレージの開始位置。 flat[offset] から flat[offset 15] まで格納されます。
関数 getPosition() および setPosition() は、行列オブジェクトの位置コンポーネントを取得または設定するために使用されます。回転コンポーネントが左上隅の 3x3 サブマトリックスに格納されるのと同様に、位置コンポーネントは 4 行目の最初の 3 つのコンポーネント、つまり element[12]、element[13]、element[14] に格納されます。
関数 getColumeX()、getColumeY()、および getColumeZ() はそれぞれ、左上隅の 3×3 部分行列の 3 つの列を抽出します。
関数compose(translate,rotation,scale)は、vector3型translateオブジェクトで表現される平行移動、matrix3型回転オブジェクトで表現される回転、vector3型scaleオブジェクトで表現されるスケーリングを組み合わせるオブジェクト行列を設定します。変換行列。実際、これは、モデル行列の対応する部分空間に直接埋められることを意味します。
関数 decompose(translate,rotation,scale) は、行列オブジェクトを 3 つのオブジェクトに分割します。これは、前の関数とまったく逆です。
関数 extractPosition(m) および extractRotation(m) は、行列オブジェクト m 内の位置または回転を表すコンポーネントを呼び出し元オブジェクトに抽出します。たとえば、2 つのオブジェクトは複数の異なる変換を受けており、オブジェクトのモデルのみが抽出されます。ビュー行列が別のオブジェクトのモデル ビュー行列を回転させる場合、呼び出し元は他のオブジェクトと同じ回転方向を維持します。
関数translate(v)は、モデル行列の最も基本的な変換の1つである平行移動変換であり、モデル行列がベクトルvによって従属するオブジェクトを平行移動します。
関数rotateX(angle)、rotateY(angle)、およびrotateZ(angle)はそれぞれ、モデル行列が属するオブジェクトをX、Y、Z軸の周りで角度ごとに回転させます。
関数rotateByAxis(axis, angle)は、モデル行列が属するオブジェクトを任意の軸の周りで角度だけ回転させます。これは、関係する2つの変換の多重重ね合わせです(重ね合わせパラメータは現在の変換で構成されます)。位置と軸パラメータの決定)、任意の軸を中心とした回転の問題については、「モデル ビュー マトリックスと投影マトリックス: WebGL ノート (1)」で説明しました。
ここにスケール関数があるべきではないでしょうか?しかし、ソースコードからは見つかりませんでした。
関数 makeTranslate(x,y,z)、makeRotationX(theta)、makeRotationY(theta)、makeRotationZ(theta)、makeRotationAxis(axis,angle)、および makeScale(s) 関数は、オブジェクト行列を単位に直接リセットします。行列。変換、軸を中心とした回転、または単純なスケーリング後の行列。この関数はオブジェクト自体の値を更新します。更新された結果はオブジェクトの以前の値とは何の関係もありません (これは make prefix 関数の特徴でもあります)。
関数 makeFrustum(...)、makePerspective(...)、makeOrthographic(...) も新しい行列の初期化に使用されます。具体的な意味についてはカメラ クラスで説明すると思います。カメラクラスのコンストラクター これらの関数は必ず呼び出されます。
関数 clone() は行列オブジェクトをコピーして返します。
Core::Face3
この関数は三角形の平面オブジェクトを作成します
THREE.Face3 = function (a, b, c,normal, color,materialIndex ) {
this.a = a
this.b = b; 🎜 >this.c = c;
this.normal = THREE.Vector3 の通常のインスタンス : new THREE.Vector3();
this.vertexNormals = 配列の通常のインスタンス : [ ]; . color = THREE.Color のインスタンス color : new THREE.Color();
this.vertexTangents = []; =materialIndex;
this.centroid = new
};
オブジェクトの a、b、c の値は 3 つの頂点のインデックスです(後で説明します。すべてのポイントは Mesh オブジェクトに配列として保存されます); 名前が示すように、normal は法線、color は頂点マテリアルのインデックスです。これらのパラメータは、vector3 のいずれかで渡すことができます。型または配列型。
clone(x) メソッドは、同じ値を持つ新しいオブジェクトを返します。
この関数は、Face3 とほぼ同じなので省略した 4 頂点の面を作成します。
Core::Math
THREE.Math はコンストラクターを持たない「静的クラス」であるため、new キーワードを使用して初期化する必要はありません。このクラスは、必要な数学ツールをいくつか提供します。
関数clamp(x,a,b)は区間[a,b]内のxをクランプします。 ClampBottom(x,a) は、片側のみをクランプすることを除いて、同様の機能を持ちます。 関数mapLinear(x,a1,a2,b1,b2)は、点(x,y)が(a1,a2)と(b1,b2)を結ぶ直線上に位置するような値yを計算します。
コードをコピー
関数random16()、randInt(low, high)、randFloat(low, high)、およびrandFloatSpread(range)はそれぞれ、[0,1]間隔で16ビットのランダムな浮動小数点数を生成し、間隔でランダムな整数を生成します。 [low, high] 間隔。[low,high] 間隔内のランダムな浮動小数点数、[-range/2, range/2] 間隔内のランダムな浮動小数点数。
関数 sigh(x) は、x の符号に応じて 1 または -1 を返します。
Core::Clock
このコンストラクターはクロック (正確にはストップウォッチ) オブジェクトを作成します
THREE.Clock = function ( autoStart ) {
this.autoStart = ( autoStart !== unknown ) : true; this.startTime = 0;
this.running = 0;
関数) と stop() は、タイミングを開始または停止するために使用されます。
関数 getDelta() は、関数が最後に呼び出されてからの時間を返します。関数が初めて呼び出された場合は、計時を開始してからの時間の長さを返します。 autoStart 値が true の場合、getDelta() 関数の呼び出し時に start() 関数が呼び出されていないか、stop() 関数が呼び出されている場合、タイミングは自動的に開始され、0 が返されます。 autoStart() が false の場合、start() を呼び出す前または stop() を呼び出した後に getDelta() を呼び出すと 0 が返されます。
Core::Color
このコンストラクターは、色を表すオブジェクトを構築します
コードをコピー
関数 setHex(hex) は、オブジェクトの r、g、b 属性を 16 進数で設定します。実際、オブジェクトでは、色は最終的にこれら 3 つの属性に格納されます。
コードをコピー
return this
},
関数 setRGB(r,g,b) および setHSV(h,s) ,v) RGB 値または HSV 値でオブジェクトを設定します。
関数 getHex() は 16 進数のカラー値を返します。
関数 copyGammaToLinear(color) と copyLinearToGamma(color) は、それぞれ色の RGB 値を二乗またはルートし、呼び出し元オブジェクトに割り当てます。
関数convertGammaToLinear()とconvertLinearToGamma()はそれぞれ、呼び出し元独自のRGB値に対して二乗またはオープンされます。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7342
7342
 9
9
 1627
1627
 14
14
 1352
1352
 46
46
 1265
1265
 25
25
 1210
1210
 29
29
 JavaScriptの文字列文字を交換します
Mar 11, 2025 am 12:07 AM
JavaScriptの文字列文字を交換します
Mar 11, 2025 am 12:07 AM
JavaScript文字列置換法とFAQの詳細な説明 この記事では、javaScriptの文字列文字を置き換える2つの方法について説明します:内部JavaScriptコードとWebページの内部HTML。 JavaScriptコード内の文字列を交換します 最も直接的な方法は、置換()メソッドを使用することです。 str = str.replace( "find"、 "置換"); この方法は、最初の一致のみを置き換えます。すべての一致を置き換えるには、正規表現を使用して、グローバルフラグGを追加します。 str = str.replace(/fi
 カスタムGoogle検索APIセットアップチュートリアル
Mar 04, 2025 am 01:06 AM
カスタムGoogle検索APIセットアップチュートリアル
Mar 04, 2025 am 01:06 AM
このチュートリアルでは、カスタムGoogle検索APIをブログまたはWebサイトに統合する方法を示し、標準のWordPressテーマ検索関数よりも洗練された検索エクスペリエンスを提供します。 驚くほど簡単です!検索をyに制限することができます
 独自のAjax Webアプリケーションを構築します
Mar 09, 2025 am 12:11 AM
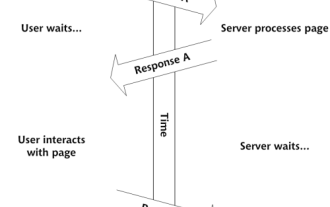
独自のAjax Webアプリケーションを構築します
Mar 09, 2025 am 12:11 AM
それで、あなたはここで、Ajaxと呼ばれるこのことについてすべてを学ぶ準備ができています。しかし、それは正確には何ですか? Ajaxという用語は、動的でインタラクティブなWebコンテンツを作成するために使用されるテクノロジーのゆるいグループ化を指します。 Ajaxという用語は、もともとJesse Jによって造られました
 例JSONファイルの例
Mar 03, 2025 am 12:35 AM
例JSONファイルの例
Mar 03, 2025 am 12:35 AM
この記事シリーズは、2017年半ばに最新の情報と新鮮な例で書き直されました。 このJSONの例では、JSON形式を使用してファイルに単純な値を保存する方法について説明します。 キー価値ペア表記を使用して、あらゆる種類を保存できます
 8見事なjQueryページレイアウトプラグイン
Mar 06, 2025 am 12:48 AM
8見事なjQueryページレイアウトプラグイン
Mar 06, 2025 am 12:48 AM
楽なWebページレイアウトのためにjQueryを活用する:8本質的なプラグイン jQueryは、Webページのレイアウトを大幅に簡素化します。 この記事では、プロセスを合理化する8つの強力なjQueryプラグイン、特に手動のウェブサイトの作成に役立ちます
 ' this' JavaScriptで?
Mar 04, 2025 am 01:15 AM
' this' JavaScriptで?
Mar 04, 2025 am 01:15 AM
コアポイント これは通常、メソッドを「所有」するオブジェクトを指しますが、関数がどのように呼び出されるかに依存します。 現在のオブジェクトがない場合、これはグローバルオブジェクトを指します。 Webブラウザでは、ウィンドウで表されます。 関数を呼び出すと、これはグローバルオブジェクトを維持しますが、オブジェクトコンストラクターまたはそのメソッドを呼び出すとき、これはオブジェクトのインスタンスを指します。 call()、apply()、bind()などのメソッドを使用して、このコンテキストを変更できます。これらのメソッドは、与えられたこの値とパラメーターを使用して関数を呼び出します。 JavaScriptは優れたプログラミング言語です。数年前、この文はそうでした
 ソースビューアーでjQueryの知識を向上させます
Mar 05, 2025 am 12:54 AM
ソースビューアーでjQueryの知識を向上させます
Mar 05, 2025 am 12:54 AM
jQueryは素晴らしいJavaScriptフレームワークです。ただし、他のライブラリと同様に、何が起こっているのかを発見するためにフードの下に入る必要がある場合があります。おそらく、バグをトレースしているか、jQueryが特定のUIをどのように達成するかに興味があるからです
 モバイル開発用のモバイルチートシート10個
Mar 05, 2025 am 12:43 AM
モバイル開発用のモバイルチートシート10個
Mar 05, 2025 am 12:43 AM
この投稿は、Android、BlackBerry、およびiPhoneアプリ開発用の有用なチートシート、リファレンスガイド、クイックレシピ、コードスニペットをコンパイルします。 開発者がいないべきではありません! タッチジェスチャーリファレンスガイド(PDF) Desigの貴重なリソース




