バレンタインデー限定、純粋な js スクリプト 1k サイズ 3D バラ効果_javascript スキル

前年圣诞节上，西班牙程序员Roman Cortes带来了用纯javascript脚本编写的神奇3D圣诞树，令人印象深刻。2月14日情人节就要来临了，还是Roman Cortes，这次他又带来了用javascript脚本编写的红色玫瑰花。用代码做出的玫瑰花，这才是牛逼程序员送给女友的最好情人节礼物呢！(提示：在不同浏览器下观看效果、速度会有很大的不同)
图片是由代码生成，用户可以刷新该页面，重复观看这朵玫瑰的呈现过程。

3D玫瑰花的实现代码如下：

with(m=Math)C=cos,S=sin,P=pow,R=random;c.width=c.height=f=500;h=-250;function p(a,b,c){if(c>60)return[S(a*7)*(13+5/(.2+P(b*4,4)))-S(b)*50,b*f+50,625+C(a*7)*(13+5/(.2+P(b*4,4)))+b*400,a*1-b/2,a];A=a*2-1;B=b*2-1;if(A*A+B*B<1){if(c>37){n=(j=c&1)?6:4;o=.5/(a+.01)+C(b*125)*3-a*300;w=b*h;return[o*C(n)+w*S(n)+j*610-390,o*S(n)-w*C(n)+550-j*350,1180+C(B+A)*99-j*300,.4-a*.1+P(1-B*B,-h*6)*.15-a*b*.4+C(a+b)/5+P(C((o*(a+1)+(B>0?w:-w))/25),30)*.1*(1-B*B),o/1e3+.7-o*w*3e-6]}if(c>32){c=c*1.16-.15;o=a*45-20;w=b*b*h;z=o*S(c)+w*C(c)+620;return[o*C(c)-w*S(c),28+C(B*.5)*99-b*b*b*60-z/2-h,z,(b*b*.3+P((1-(A*A)),7)*.15+.3)*b,b*.7]}o=A*(2-b)*(80-c*2);w=99-C(A)*120-C(b)*(-h-c*4.9)+C(P(1-b,7))*50+c*2;z=o*S(c)+w*C(c)+700;return[o*C(c)-w*S(c),B*99-C(P(b, 7))*50-c/3-z/1.35+450,z,(1-b/1.2)*.9+a*.1, P((1-b),20)/4+.05]}}setInterval('for(i=0;i<1e4;i++)if(s=p(R(),R(),i%46/.74)){z=s[2];x=~~(s[0]*f/z-h);y=~~(s[1]*f/z-h);if(!m[q=y*f+x]|m[q]>z)m[q]=z,a.fillStyle="rgb("+~(s[3]*h)+","+~(s[4]*h)+","+~(s[3]*s[3]*-80)+")",a.fillRect(x,y,1,1)}',0)

当然，感兴趣的人可以了解下面的实现过程与相关理论：

这朵三维代码玫瑰的呈现效果采用了蒙特卡罗方法，创造者对蒙特卡罗方法非常推崇，他表示在功能优化和采样方面，蒙特卡罗方法是“令人难以置信的强大工具”。关于蒙特卡罗方法可以参考：Monte Carlo method 。

具体操作：

外观采样呈现效果绘制

我用了多个不同的形状图来组成这朵代码玫瑰。共使用了31个形状：24个花瓣，4个萼片，2个叶子和1根花茎，其中每一个形状图都用代码进行描绘。

首先，来定义一个采样范围：

function surface(a, b) { // I'm using a and b as parameters ranging from 0 to 1.

return {

x: a*50,

y: b*50

};

// this surface will be a square of 50x50 units of size

}

然后，编写形状描绘代码：

var canvas = document.body.appendChild(document.createElement("canvas")),

context = canvas.getContext("2d"),

a, b, position;

// Now I'm going to sample the surface at .1 intervals for a and b parameters:

for (a = 0; a < 1; a += .1) {

for (b = 0; b < 1; b += .1) {

position = surface(a, b);

context.fillRect(position.x, position.y, 1, 1);

}

}

这时，看到的效果是这样的：

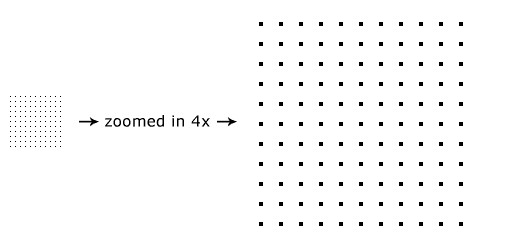
现在，尝试一下更密集的采样间隔：

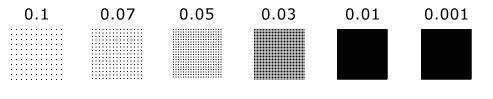
正如现在所看到的，因为采样间隔越来越密集，点越来越接近，到最高密度时，相邻点之间的距离小于一个像素，肉眼就看不到间隔（见0.01）。为了不造成太大的视觉差，再进一步缩小采样间隔，此时，绘制区已经填满（比较结果为0.01和0.001）。

接下来，我用这个公式来绘制一个圆形：（X-X0）^ 2 +（Y-Y0）^ 2 <半径^ 2，其中（X0，Y0）为圆心：

function surface(a, b) {

var x = a * 100,

y = b * 100,

radius = 50,

x0 = 50,

y0 = 50;

if ((x - x0) * (x - x0) + (y - y0) * (y - y0) < radius * radius) {

// inside the circle

return {

x: x,

y: y

};

} else {

// outside the circle

return null;

}

}

为了防止溢出，还要加上一个采样条件：

if (position = surface(a, b)) {

context.fillRect(position.x, position.y, 1, 1);

}

结果如下：

有不同的方法来定义一个圆，其中一些并不需要拒绝采样。我并无一定要使用哪一种来定义圆圈的意思，所以下面用另一种方法来定义一个圆：

function surface(a, b) {

// Circle using polar coordinates

var angle = a * Math.PI * 2,

radius = 50,

x0 = 50,

y0 = 50;

return {

x: Math.cos(angle) * radius * b + x0,

y: Math.sin(angle) * radius * b + y0

};

}

如图：

（此方法相比前一个方法需要密集采样以进行填充。）

好了，现在让圆变形，以使它看起来更像是一个花瓣：

function surface(a, b) {

var x = a * 100,

y = b * 100,

radius = 50,

x0 = 50,

y0 = 50;

if ((x - x0) * (x - x0) + (y - y0) * (y - y0) < radius * radius) {

return {

x: x,

y: y * (1 + b) / 2 // deformation

};

} else {

return null;

}

}

结果：

这看起来已经很像一个玫瑰花瓣的形状了。在这里也可以试试通过修改一些函数数值，将会出现很多有趣的形状。

接下来应该给它添加色彩了：

function surface(a, b) {

var x = a * 100,

y = b * 100,

radius = 50,

x0 = 50,

y0 = 50;

if ((x - x0) * (x - x0) + (y - y0) * (y - y0) < radius * radius) {

return {

x: x,

y: y * (1 + b) / 2,

r: 100 + Math.floor((1 - b) * 155), // this will add a gradient

g: 50,

b: 50

};

} else {

return null;

}

}

for (a = 0; a < 1; a += .01) {

for (b = 0; b < 1; b += .001) {

if (point = surface(a, b)) {

context.fillStyle = "rgb(" + point.r + "," + point.g + "," + point.b + ")";

context.fillRect(point.x, point.y, 1, 1);

}

}

}

结果：

一片带色的花瓣就出现了。

3D曲面和透视投影

定义三维表面很简单，比如，来定义一个管状物体：

function surface(a, b) {

var angle = a * Math.PI * 2,

radius = 100,

length = 400;

return {

x: Math.cos(angle) * radius,

y: Math.sin(angle) * radius,

z: b * length - length / 2, // by subtracting length/2 I have centered the tube at (0, 0, 0)

r: 0,

g: Math.floor(b * 255),

b: 0

};

}

接着添加投影透视图，首先需要我们定义一个摄像头：

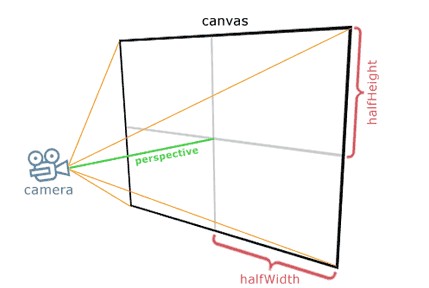
如上图，将摄像头放置在（0，0，Z）位置，画布在X / Y平面。投影到画布上的采样点为：

var pX, pY, // projected on canvas x and y coordinates

perspective = 350,

halfHeight = canvas.height / 2,

halfWidth = canvas.width / 2,

cameraZ = -700;

for (a = 0; a < 1; a += .001) {

for (b = 0; b < 1; b += .01) {

if (point = surface(a, b)) {

pX = (point.x * perspective) / (point.z - cameraZ) + halfWidth;

pY = (point.y * perspective) / (point.z - cameraZ) + halfHeight;

context.fillStyle = "rgb(" + point.r + "," + point.g + "," + point.b + ")";

context.fillRect(pX, pY, 1, 1);

}

}

}

效果为：

z-buffer

z-buffer在计算机图形学中是一个相当普遍的技术，在为物件进行着色时，执行“隐藏面消除”工作，使隐藏物件背后的部分就不会被显示出来。

上图是用z-buffer技术处理后的玫瑰。(可以看到已经具有立体感了)

代码如下：

var zBuffer = [],

zBufferIndex;

for (a = 0; a < 1; a += .001) {

for (b = 0; b < 1; b += .01) {

if (point = surface(a, b)) {

pX = Math.floor((point.x * perspective) / (point.z - cameraZ) + halfWidth);

pY = Math.floor((point.y * perspective) / (point.z - cameraZ) + halfHeight);

zBufferIndex = pY * canvas.width + pX;

if ((typeof zBuffer[zBufferIndex] === "undefined") || (point.z < zBuffer[zBufferIndex])) {

zBuffer[zBufferIndex] = point.z;

context.fillStyle = "rgb(" + point.r + "," + point.g + "," + point.b + ")";

context.fillRect(pX, pY, 1, 1);

}

}

}

}

旋转

你可以使用任何矢量旋转的方法。在代码玫瑰的创建中，我使用的是欧拉旋转。现在将之前编写的管状物进行旋转，实现绕Y轴旋转：

function surface(a, b) {

var angle = a * Math.PI * 2,

radius = 100,

length = 400,

x = Math.cos(angle) * radius,

y = Math.sin(angle) * radius,

z = b * length - length / 2,

yAxisRotationAngle = -.4, // in radians!

rotatedX = x * Math.cos(yAxisRotationAngle) + z * Math.sin(yAxisRotationAngle),

rotatedZ = x * -Math.sin(yAxisRotationAngle) + z * Math.cos(yAxisRotationAngle);

return {

x: rotatedX,

y: y,

z: rotatedZ,

r: 0,

g: Math.floor(b * 255),

b: 0

};

}

効果:

モンテカルロ法

サンプリング時間については、間隔が大きすぎたり小さすぎたりすると、視覚的に非常に悪くなるため、ここではモンテカルロ法を使用します。

var i;

window.setInterval(function () {

for (i = 0; i < 10000; i ) {

if (point = surface(Math.random(), Math.random())) {

pX = Math.floor((point.x * perspective) / (point.z - cameraZ) halfWidth);

pY = Math.floor((point.y * perspective) / (point.z - cameraZ) halfHeight);

zBufferIndex = pY * canvas.width pX;

if ((typeof zBuffer[zBufferIndex] === "undefined") || (point.z < zBuffer[zBufferIndex])) {

zBuffer[zBufferIndex] = point.z;

context.fillStyle = "rgb(" point.r "," point.g "," point.b ")";

context.fillRect(pX, pY, 1, 1);

}

}

}

}, 0);

変数 i;

window.setInterval(function () {

for (i = 0; i

if (point = surface(Math.random(), Math.random())) {

pX = Math.floor((point.x * 視点) / (point.z - カメラ Z)halfWidth);

pY = Math.floor((point.y * 視点) / (point.z - カメラ Z)halfHeight);

zBufferIndex = pY * Canvas.width pX;

if ((typeof zBuffer[zBufferIndex] === "未定義") || (point.z < zBuffer[zBufferIndex])) {

zBuffer[zBufferIndex] = point.z;

context.fillStyle = "rgb(" point.r "," point.g "," point.b ")";

context.fillRect(pX, pY, 1, 1);

}

}

}

}, 0);

a と b をランダム パラメーターとして設定し、表面の充填を完了するのに十分なサンプルを使用します。一度に 10,000 ポイントを描画し、画面の更新が完了するのを待ちます。

もう 1 つ注意すべき点は、乱数が間違っている場合、表面の塗りつぶし効果も間違っているということです。一部のブラウザでは、Math.random の実行が線形であるため、表面の塗りつぶし効果でエラーが発生する可能性があります。現時点では、エラーを避けるためにメルセンヌ ツイスター (乱数アルゴリズム) などを使用して高品質の PRNG サンプリングを実行する必要があります。 完了 バラの各部分を同時に完成させてレンダリングするには、各部分に同期用の値を返すパラメーターを設定する関数を追加する必要もあります。そして、区分関数を使用してバラのさまざまな部分を表します。たとえば、花びらは回転と変形を使用して作成しました。 表面サンプリング法は、3 次元グラフィックスを作成するための最も有名かつ最も古い方法の 1 つですが、表面サンプリングにモンテカルロと Z バッファーを追加するこの方法は一般的ではありません。現実のシーンを制作する場合、これはあまり創造的ではないかもしれませんが、コードの実装が単純でサイズが小さいため、それでも満足のいくものです。 この記事が、コンピュータ グラフィックスの愛好家にさまざまなレンダリング方法を試して楽しんでもらうきっかけになれば幸いです。 (ロマン・コルテス) 英語の元のアドレス: romancortes.com