単一ストリーム最短パス (ダイクストラ アルゴリズム) php 実装
単一ソースの最短パス (ダイクストラ アルゴリズム) PHP 実装 2. dist を更新します。直接隣接する頂点の値。 (dist[j]=min{dist[j],dist[i]+cost[i][j]}) 3. U=V がわかったら停止します。 PHP の固有のプロパティを使用したコードは次のとおりです。
単一ソースの最短パス アルゴリズムが症例スコアリングに使用される医療プロジェクトを実行します。単一ソース最短経路のダイクストラ アルゴリズムの考え方は次のとおりです。
i から j への最短経路 (Vi...Vk, Vj) がある場合、 VkはVjの前の頂点である。したがって、(Vi...Vk) も i から k への最短経路でなければなりません。ダイクストラは、最短経路の長さを増加させながら、最短経路を次々に生成するアルゴリズムです。たとえば、ソース頂点 V0 の場合、最初に直接隣接する頂点の中で最も長さが短い頂点 Vi を選択します。その後、V0 から Vj 頂点までの最短距離 dist[j]=min{dist[j] が現在わかっています。 ,dist[i]+cost[i][j]}。 G=
1. V-U から dist[i] 値を最小にする頂点 i を選択し、i を U に追加します。function dijkstra(){ $node_info_arr=array( //结点的邻接表结构 array( 'node_id'=>0, //某个结点的id 'next_node'=>array(4,2,1), 'node_type'=>0, 'cost'=>array(10,30,100) ), array( 'node_id'=>4, //某个结点的id 'next_node'=>array(3), 'node_type'=>1, 'cost'=>array(50) ), array( 'node_id'=>3, //某个结点的id 'next_node'=>array(1), 'node_type'=>1, 'cost'=>array(10) ), array( 'node_id'=>2, //某个结点的id 'next_node'=>array(3,1), 'node_type'=>1, 'cost'=>array(60,60) ), array( 'node_id'=>1, //某个结点的id 'next_node'=>array(), 'node_type'=>2, 'cost'=>array() ) ); $start_node_id=false; //起始结点id $i_cost=array(array()); //两个节点之间的开销 $i_dist=array(); //起始点到各点的最短距离 $b_mark=array(); //是否加入了 foreach($node_info_arr as &$node_info){ if($node_info['node_type']==0){ $start_node_id=$node_info['node_id']; //找到初始节点 } foreach($node_info['next_node'] as $key=>$next_node){ $i_cost[$node_info['node_id']][$next_node]=$node_info['cost'][$key]; } $i_dist[$node_info['node_id']]='INF'; //初始化为无穷大 $b_mark[$node_info['node_id']]=false; //初始化未加入 } if($start_node_id===false){ return '302'; } //计算初始结点到各节点的最短路径 $i_dist[$start_node_id]=0; //初始点到其本身的距离为0 $b_mark[$start_node_id]=true; //初始点加入集合 $current_node_id=$start_node_id; //最近加入的节点id $node_count=count($node_info_arr); for($i=0;$i<$node_count;$i++){ $min='INF'; //当前节点的最近距离 if(is_array($i_cost[$current_node_id])){ foreach($i_cost[$current_node_id] as $key=>$val){ if($i_dist[$key]=='INF'||$i_dist[$key]>$i_dist[$current_node_id]+$val){ $i_dist[$key]=$i_dist[$current_node_id]+$val; } } } foreach($i_dist as $key=>$val){ if(!$b_mark[$key]){ if($val!='INF'&&($min=='INF'||$min>$val)){ $min=$val; $candidate_node_id=$key; //候选最近结点id } } } if($min=='INF'){ break; } $current_node_id=$candidate_node_id; $b_mark[$current_node_id]=true; } foreach($i_dist as $key=>$val){ echo $start_node_id.'=>'.$key.':'.$val.'<br />'; }}
例を示します。画像内:


実行結果は次のとおりです:
0=>0:0
0=>4:10
0=>3: 60
0=> ;2:30
0=>1:70
転載元:カンルイ族 ? >単一ソースの最短パス php 実装

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7563
7563
 15
15
 1385
1385
 52
52
 84
84
 11
11
 28
28
 99
99
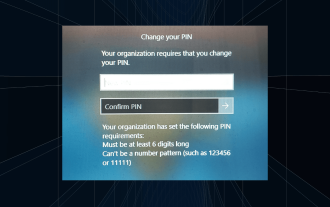 解決策: 組織では PIN を変更する必要があります。
Oct 04, 2023 pm 05:45 PM
解決策: 組織では PIN を変更する必要があります。
Oct 04, 2023 pm 05:45 PM
ログイン画面に「組織から PIN の変更を求められています」というメッセージが表示されます。これは、個人のデバイスを制御できる組織ベースのアカウント設定を使用しているコンピューターで PIN の有効期限の制限に達した場合に発生します。ただし、個人アカウントを使用して Windows をセットアップした場合、エラー メッセージは表示されないのが理想的です。常にそうとは限りませんが。エラーが発生したほとんどのユーザーは、個人アカウントを使用して報告します。私の組織が Windows 11 で PIN を変更するように要求するのはなぜですか?アカウントが組織に関連付けられている可能性があるため、主なアプローチはこれを確認することです。ドメイン管理者に問い合わせると解決できます。さらに、ローカル ポリシー設定が間違っていたり、レジストリ キーが間違っていたりすると、エラーが発生する可能性があります。今すぐ
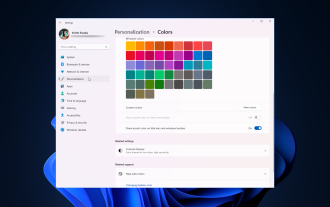 Windows 11 でウィンドウの境界線の設定を調整する方法: 色とサイズを変更する
Sep 22, 2023 am 11:37 AM
Windows 11 でウィンドウの境界線の設定を調整する方法: 色とサイズを変更する
Sep 22, 2023 am 11:37 AM
Windows 11 では、新鮮でエレガントなデザインが前面に押し出されており、最新のインターフェイスにより、ウィンドウの境界線などの細部をカスタマイズして変更することができます。このガイドでは、Windows オペレーティング システムで自分のスタイルを反映した環境を作成するのに役立つ手順について説明します。ウィンドウの境界線の設定を変更するにはどうすればよいですか? + を押して設定アプリを開きます。 Windows [個人用設定] に移動し、[色の設定] をクリックします。ウィンドウの境界線の色の変更設定ウィンドウ 11" width="643" height="500" > [タイトル バーとウィンドウの境界線にアクセント カラーを表示する] オプションを見つけて、その横にあるスイッチを切り替えます。 [スタート] メニューとタスク バーにアクセント カラーを表示するにはスタート メニューとタスク バーにテーマの色を表示するには、[スタート メニューとタスク バーにテーマを表示] をオンにします。
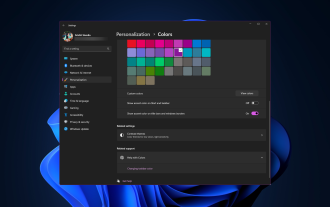 Windows 11でタイトルバーの色を変更するにはどうすればよいですか?
Sep 14, 2023 pm 03:33 PM
Windows 11でタイトルバーの色を変更するにはどうすればよいですか?
Sep 14, 2023 pm 03:33 PM
デフォルトでは、Windows 11 のタイトル バーの色は、選択したダーク/ライト テーマによって異なります。ただし、任意の色に変更できます。このガイドでは、デスクトップ エクスペリエンスを変更し、視覚的に魅力的なものにするためにカスタマイズする 3 つの方法について、段階的な手順を説明します。アクティブなウィンドウと非アクティブなウィンドウのタイトル バーの色を変更することはできますか?はい、設定アプリを使用してアクティブなウィンドウのタイトル バーの色を変更したり、レジストリ エディターを使用して非アクティブなウィンドウのタイトル バーの色を変更したりできます。これらの手順を学習するには、次のセクションに進んでください。 Windows 11でタイトルバーの色を変更するにはどうすればよいですか? 1. 設定アプリを使用して + を押して設定ウィンドウを開きます。 Windows「個人用設定」に進み、
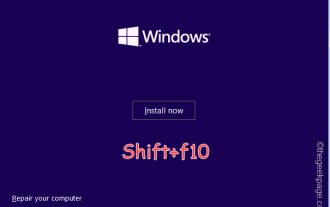 Windows 11/10修復におけるOOBELANGUAGEエラーの問題
Jul 16, 2023 pm 03:29 PM
Windows 11/10修復におけるOOBELANGUAGEエラーの問題
Jul 16, 2023 pm 03:29 PM
Windows インストーラー ページに「問題が発生しました」というメッセージとともに「OOBELANGUAGE」というメッセージが表示されますか?このようなエラーが原因で Windows のインストールが停止することがあります。 OOBE とは、すぐに使えるエクスペリエンスを意味します。エラー メッセージが示すように、これは OOBE 言語の選択に関連する問題です。心配する必要はありません。OOBE 画面自体から気の利いたレジストリ編集を行うことで、この問題を解決できます。クイックフィックス – 1. OOBE アプリの下部にある [再試行] ボタンをクリックします。これにより、問題が発生することなくプロセスが続行されます。 2. 電源ボタンを使用してシステムを強制的にシャットダウンします。システムの再起動後、OOBE が続行されます。 3. システムをインターネットから切断します。 OOBE のすべての側面をオフライン モードで完了する
 Windows 11 でタスクバーのサムネイル プレビューを有効または無効にする方法
Sep 15, 2023 pm 03:57 PM
Windows 11 でタスクバーのサムネイル プレビューを有効または無効にする方法
Sep 15, 2023 pm 03:57 PM
タスクバーのサムネイルは楽しい場合もありますが、気が散ったり煩わしい場合もあります。この領域にマウスを移動する頻度を考えると、重要なウィンドウを誤って閉じてしまったことが何度かある可能性があります。もう 1 つの欠点は、より多くのシステム リソースを使用することです。そのため、リソース効率を高める方法を探している場合は、それを無効にする方法を説明します。ただし、ハードウェアの仕様が対応可能で、プレビューが気に入った場合は、有効にすることができます。 Windows 11でタスクバーのサムネイルプレビューを有効にする方法は? 1. 設定アプリを使用してキーをタップし、[設定] をクリックします。 Windows では、「システム」をクリックし、「バージョン情報」を選択します。 「システムの詳細設定」をクリックします。 [詳細設定] タブに移動し、[パフォーマンス] の下の [設定] を選択します。 「視覚効果」を選択します
 Windows 11 でのディスプレイ スケーリング ガイド
Sep 19, 2023 pm 06:45 PM
Windows 11 でのディスプレイ スケーリング ガイド
Sep 19, 2023 pm 06:45 PM
Windows 11 のディスプレイ スケーリングに関しては、好みが人それぞれ異なります。大きなアイコンを好む人もいれば、小さなアイコンを好む人もいます。ただし、適切なスケーリングが重要であることには誰もが同意します。フォントのスケーリングが不十分であったり、画像が過度にスケーリングされたりすると、作業中の生産性が大幅に低下する可能性があるため、システムの機能を最大限に活用するためにカスタマイズする方法を知る必要があります。カスタム ズームの利点: これは、画面上のテキストを読むのが難しい人にとって便利な機能です。一度に画面上でより多くの情報を確認できるようになります。特定のモニターおよびアプリケーションにのみ適用するカスタム拡張プロファイルを作成できます。ローエンド ハードウェアのパフォーマンスの向上に役立ちます。画面上の内容をより詳細に制御できるようになります。 Windows 11の使用方法
 Huawei GT3 ProとGT4の違いは何ですか?
Dec 29, 2023 pm 02:27 PM
Huawei GT3 ProとGT4の違いは何ですか?
Dec 29, 2023 pm 02:27 PM
多くのユーザーはスマートウォッチを選ぶときにファーウェイブランドを選択しますが、その中でもファーウェイ GT3pro と GT4 は非常に人気のある選択肢であり、多くのユーザーはファーウェイ GT3pro と GT4 の違いに興味を持っています。 Huawei GT3pro と GT4 の違いは何ですか? 1. 外観 GT4: 46mm と 41mm、材質はガラスミラー + ステンレススチールボディ + 高解像度ファイバーバックシェルです。 GT3pro: 46.6mm および 42.9mm、材質はサファイアガラス + チタンボディ/セラミックボディ + セラミックバックシェルです。 2. 健全な GT4: 最新の Huawei Truseen5.5+ アルゴリズムを使用すると、結果はより正確になります。 GT3pro: ECG 心電図と血管と安全性を追加
 Windows 11で明るさを調整する10の方法
Dec 18, 2023 pm 02:21 PM
Windows 11で明るさを調整する10の方法
Dec 18, 2023 pm 02:21 PM
画面の明るさは、最新のコンピューティング デバイスを使用する上で不可欠な部分であり、特に長時間画面を見る場合には重要です。目の疲れを軽減し、可読性を向上させ、コンテンツを簡単かつ効率的に表示するのに役立ちます。ただし、設定によっては、特に新しい UI が変更された Windows 11 では、明るさの管理が難しい場合があります。明るさの調整に問題がある場合は、Windows 11 で明るさを管理するすべての方法を次に示します。 Windows 11で明るさを変更する方法【10の方法を解説】 シングルモニターユーザーは、次の方法でWindows 11の明るさを調整できます。これには、ラップトップだけでなく、単一のモニターを使用するデスクトップ システムも含まれます。はじめましょう。方法 1: アクション センターを使用する アクション センターにアクセスできる




