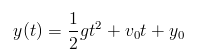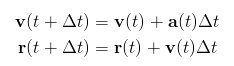JavaScript を使ってゲーム物理を遊ぶ (1) 運動学シミュレーションとパーティクルシステム

シリーズ紹介
おそらく、300 年前のアイザックニュートン卿 (1643-1727) は、今日の多くのゲームやアニメーションで物理学が広く使用されているとは想像していなかったでしょう。なぜこれらのアプリケーションで物理学を使用するのでしょうか?著者は、私たちは生まれたときから物理世界の法則を感じ、この世界で物体がどのように「正常に動くか」を認識していると考えています。たとえば、ボールを撃つとき、ボールは放物線になります（回転するボールは回転する可能性があります）。曲がったボール）、紐の端に結ばれた石は一定の周波数で振動します、など。ゲームやアニメーション内のオブジェクトがリアルに感じられるためには、私たちが期待する「通常の動き」と一致する方法でオブジェクトが動く必要があります。
今日のゲームアニメーションには、運動学シミュレーション、剛体ダイナミクスシミュレーション、ストリング/クロスシミュレーション、ソフトボディダイナミクスシミュレーション(ソフトボディダイナミクスシミュレーション)、流体ダイナミクスシミュレーション(流体力学シミュレーション)など、さまざまな物理シミュレーション技術が適用されています。、など。さらに、多くのシミュレーションシステムでは衝突検出が必要です。
このシリーズでは、この分野の最も基本的な知識をいくつか紹介し、引き続き JavaScript を例として使用し、リアルタイムのインタラクティブな方法で体験していきたいと考えています。
この記事の紹介
シリーズの最初の記事として、この記事では、非常に単純な数式が 2 つだけある、最も単純な運動学シミュレーションを紹介します。キネマティックシミュレーションは、さまざまなオブジェクト (マリオのジャンプ、砲弾など) の動きをシミュレートするために使用できます。この記事では、パーティクルシステムを使用して視覚的な特殊効果を作成します (パーティクルシステムは実際にゲームをプレイするために使用できます)。視覚的な特殊効果だけではありません)。
運動学シミュレーション
運動学では物体の動きを研究します。力学との違いは、運動学では物体の質量や慣性モーメントが考慮されないことと、物体に加えられる力やトルクが考慮されないことです。
まずニュートンの運動の第一法則を思い出してみましょう:
物体に外力が作用していないとき、または正味の力がゼロのとき、もともと静止していたものは常に静止し、元は静止していました。運動中は常に一定の速度で直線に沿って移動します。この法則は「慣性の法則」とも呼ばれます。この法則は、すべてのオブジェクトはその位置に加えて、線速度状態も持つことを示しています。ただし、力の影響を受けないオブジェクトだけをシミュレートするのは面白くありません。力の概念を脇に置いて、線形加速度を使用して物体の動きに影響を与えることができます。たとえば、任意の時刻 t における自由落下物体の y 軸座標を計算するには、次の解析ソリューションを使用できます。
JavaScript を使ってゲーム物理を遊ぶ (1) 運動学シミュレーションとパーティクルシステム_JavaScript スキル
ここで、とはそれぞれ t における y 軸座標です。 =0 の初期座標と速度、g は重力加速度です。
この解析ソリューションは単純ですが、いくつかの欠点があります。たとえば、g は定数であり、シミュレーションプロセス中に変更することはできません。また、オブジェクトが障害物に遭遇して衝突した場合、この式を適用することは困難です。この不連続性（不連続性）を処理します。
コンピューターシミュレーションでは、連続的なオブジェクトの状態を計算する必要があることがよくあります。ゲーム用語では、最初のフレームの状態、2 番目のフレームの状態などを計算することを意味します。任意の時刻 t におけるオブジェクトの状態を仮定します。位置ベクトルは、速度ベクトルは、加速度ベクトルはです。ある時点の状態から次のシミュレーション時点の状態を計算したいとします。最も簡単な方法は、数値積分にオイラー法を使用することです。
JavaScript を使ってゲーム物理を遊ぶ (1) 運動学シミュレーションとパーティクルシステム_JavaScript スキル
オイラー法は非常に単純ですが、精度と安定性の問題がありますが、この記事では無視します。この記事の例では 2 次元空間を使用します。まず、JavaScript の 2 次元ベクトルクラスを実装します。

コードをコピーします。コードは次のとおりです。

 
// Vector2.js 
Vector2 = function(x, y) { this.x = x; this.y = y }; >Vector2.prototype = { 
copy : function() { return new Vector2(this.x, this.y) }, 
length : function() { return Math.sqrt(this.x * this. x this.y * this.y ); }, 
sqrLength : function() { return this.x * this.x this.y * this.y }, 
normalize : function() { var inv = 1/this.length() ; return new Vector2(this.x * inv, this.y * inv); }, 
negate : function() { return new Vector2(-this.x, -this.y) ); }, 
add : function(v) { return new Vector2(this.x v.x, this.y v.y); }, 
subtract : function(v) { return new Vector2(this.x - v.x) , this.y - v.y); }, 
multiply : function(f) { return new Vector2(this.x * f, this.y * f) }, 
divide : function(f) { var invf = 1/f; return new Vector2(this.x * invf, this.y * invf); }, 
dot : function(v) { return this.x * v.x this.y * v.y; >}; 

Vector2.zero = new Vector2(0, 0); 


次に、HTML5 Canvas を使用してシミュレーション プロセスを表現できます。 🎜>

コードをコピーします

コードは次のとおりです:

var 位置 = 新しい Vector2(10, 200);
var 速度 = 新しい Vector2(50, -50);
var 加速 = new Vector2(0, 10);
var dt = 0.1;
function step() {
position = Position.add(velocity.multiply(dt));
速度 = Velocity.add(acceleration.multiply(dt));
ctx.ストロークスタイル = "#000000";
ctx.fillStyle = "#FFFFFF";
ctx.beginPath();
ctx.arc(position.x,position.y, 5, 0, Math.PI*2, true);
ctx.closePath();
ctx.fill();
ctx.ストローク();
}
start("kinematicsCancas", step);

<ボタン onclick="stop();" type="button">停止
<ボタン onclick="clearCanvas();" type="button">クリア

修正代网试试看

開始位置を変更

開始速度を変更(方向を含む)

加速度を変更

このプログラムの中核は step() 関数の 2 つの実行コードです。パーティクルシステムは、アニメーションやアニメーションで、雨点、火花、火花、爆発などのさまざまな効果をもたらすためによく使用されます。関連する機能は、たとえば、人が殴られた後にいくつかの光を発し、メインコーナーがそれらを吸収することができます。特性:

粒子は独立、粒子間相互不影響响(不碰撞、不徹底)

粒子有生命期間、生命结束後消滅

粒子は空間の 1 つの点として理解できますが、場合によっては、球体と環境の影響として半径を設定することもできます。

粒子帯には動作状態があり、その他の外部表示状態 (例:色、影など)もあります

粒子は回転運動を考慮せずに線性運動のみを行うことができます(例外もあります)

以下は本文例子里实现的粒子类:

复制代码

代码如下:// Particle.js Particle = function(位置、速度、寿命、色、サイズ) { this.position = 位置;

this.velocity = 速度;

this.acceleration = Vector2.zero; 
this.age = 0; 
this.life = 人生; 
this.color = カラー; 
this.size = サイズ; 
}; 

 
游戏循環环 
 粒子系统は通常 3 つの周期に分けることができます: 
 送信粒子 

模拟粒子(粒子老化、碰撞、运運動学模拟等等)
渲染パーティクル
は、ゲームループ内で各パーティクルシステムに対して上記の 3 つのステップを実行する必要があります。パーティクルを生成します。パーティクルは、数値グループの末端に追加されるだけです。 🎜>//ParticleSystem.js
function ParticleSystem() {
// プライベートフィールド
var that = this;
var 粒子 = new Array();
// パブリックフィールド
this.gravity = new Vector2(0, 100);
this.Effects = new Array();

// パブリックメソッド this.emit = function(particle) { particles.push(particle); }; // ... }

粒子は初期化時に、年 (年齢) はゼロに設定され、生命 (寿命) は固定されています。各シミュレーションが行われるたびに、都市は粒子を老化させます。つまり、年月が増加すると、年月が生命を超えて死に至ります。 🎜>

复制代码

代码如下:

function ParticleSystem() { 
// ... 
this.simulate = function(dt) { 
aging(dt); 
applyGravity(); 
applyEffectors(); 
kinematics(dt); 
}; 
// ... 
// プライベート メソッド 
function age(dt) { 
for (var i = 0; i <粒子.長さ; ) { 
var p = 粒子[i]; 
if (p.age >= p.life) 
kill(i); 🎜>else 
i ; 
} 
} 
function kill(index) { 
if (particles.length > 1) 
particles[index] =articles[particles.length - 1]; 
particles.pop(); 
} 
// ... 
} 

 
関数 kill() でトリックが使用されます。配列内のパーティクルの順序は重要ではないため、中央のパーティクルを削除するには、最後のパーティクルをその要素にコピーし、pop() を使用して最後のパーティクルを削除します。これは通常、配列の途中から要素を直接削除するよりも高速です (C の配列または std::vector にも同じことが当てはまります)。 

運動学シミュレーション
この記事の運動学シミュレーションコードの最も重要な 2 つの文をすべてのパーティクルに適用するだけです。さらに、各シミュレーションでは、まず重力加速度が粒子の加速度に書き込まれます。これは、将来的に毎回加速度を変更できるようにするために行われます (これについては、続編で説明します)。

コードをコピーコードは次のとおりです。function ParticleSystem() {

// .. .

function applyGravity() { 
for (粒子内の変数 i) 
particles[i].acceleration = that.gravity; 
function kinematics(dt) { 
for (パーティクル内の var i) { 
var p = パーティクル[i] 
p.position = p.position.add(p.velocity.multiply(dt)); 
p.velocity = p.パーティクルのレンダリング 
}円、線分 (現在位置と前の位置)、画像、スプライトなどを使用するなど、さまざまな方法でレンダリングが行われます。この記事では円を使用し、寿命と年齢の比率に応じて円の透明度を制御します。コード スニペットは次のとおりです。




コードをコピーします
。 

コードは次のとおりです。

function ParticleSystem() {
// ...

this.render = function(ctx) { for (var i粒子内) { var p = 粒子[ i]; var alpha = 1 - p.age / p.life; ctx.fillStyle = "rgba(" Math.floor(p) .color.r * 255) "," Math.floor(p.color.g * 255) ","

Math.floor(p.color.b * 255) ","

 アルファ.toFixed(2) ")"; 
 ctx.beginPath(); 
ctx.arc(p.position.x, p.position.y, p.size, 0, Math.PI * 2, true ); 
ctx.closePath(); 
ctx.fill(); 
// ... 
} 

基本的なパーティクル システムが完成しました
以下の例では、各フレームがパーティクルを放出します。その位置はキャンバスの中央 (200,200)、放出方向は 360 度、速度は 100、ライフは 1 です。 2 番目の色は赤、半径は 5 ピクセルです。 

コードをコピーします

 コードは次のとおりです。