大学のコンテストの質問 D PHP は世界で最高の言語です (2 部グラフの色付け + 再帰)
質問の主な目的は、グラフを与え、それが二部グラフであるかどうかを判断するように求めることです。そうであれば、二部グラフの 2 つのノード セット間の最小の差を見つけます。
二人が喧嘩しない場合、辺を結んでグラフを作り、このグラフの逆グラフをとります。これらの逆グラフ
の間にエッジが存在するということは、この 2 人が同じチームに所属できないことを意味します。まず、二部染色を使用して、反転画像を二部画像に変換できるかどうかを確認します。
二部グラフに染めることができたら、二部グラフの各色の人数を記録します。ユニコムの一部コンポーネントで白/黒の交換が可能です。
次に、 dp[i][j] = 1 を使用して、最初に接続された i 個のコンポーネントが j 人の人数でチームを形成できることを示します。
次に、 dp[num][s] を走査して、最小の差、答えを出力します。num は連結成分の数です。
コードは次のとおりです:
#include<cstdio> #include<cstring> #include<cmath> #include<cstdlib> #include<iostream> #include<algorithm> #include<vector> #include<map> #include<queue> #include<stack> #include<string>#include<map> #include<set>using namespace std; #define LL long long const int maxn = 100 + 5;const int INF = 1000000000;int color[maxn];//vector<int> G[maxn];int G[maxn][maxn];int one, two, num[maxn][2], n;int d[maxn][maxn];bool bipartite(int u) { //判断节点u所在的联通分量是否为二分图 if(color[u] == 1) one++; else two++; for(int v = 1; v <= n; v++) { if(G[u][v] && u != v) { if(color[u] == color[v]) return false; if(!color[v]) { color[v] = 3 - color[u]; if(!bipartite(v)) return false; } } } return true;} int main() { freopen("input.txt", "r", stdin); int t; scanf("%d", &t); while(t--) { memset(d, 0, sizeof(d)); memset(color, 0, sizeof(color)); int m; scanf("%d%d", &n, &m); for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) G[i][j] = 1; for(int i = 0; i < m; i++) { int u, v; scanf("%d%d", &u, &v); if(G[u][v]) G[u][v] = G[v][u] = 0; } int cnt = 0, tag = 1; for(int i = 1; i <=n; i++) { if(!color[i]) { one = 0, two = 0; color[i] = 1; if(!bipartite(i)) { tag = 0; break; } num[cnt][0] = one; num[cnt][1] = two; cnt++; } } if(!tag) printf("No solution\n"); else { for(int i = 0; i < cnt; i++) { if(i == 0) d[i][num[i][0]] = d[i][num[i][1]] = 1; else for(int j = 0; j <= n; j++) if(d[i - 1][j]) d[i][j + num[i][0]] = d[i][j + num[i][1]] = 1; } int ans = 1; for(int i = n/2; i; i--) if(d[cnt - 1][i]) { ans = i; break; } printf("%d\n", ans); } } return 0;} ??

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
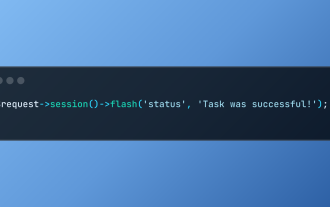 Laravelでフラッシュセッションデータを使用します
Mar 12, 2025 pm 05:08 PM
Laravelでフラッシュセッションデータを使用します
Mar 12, 2025 pm 05:08 PM
Laravelは、直感的なフラッシュメソッドを使用して、一時的なセッションデータの処理を簡素化します。これは、アプリケーション内に簡単なメッセージ、アラート、または通知を表示するのに最適です。 データは、デフォルトで次の要求のためにのみ持続します。 $リクエスト -
 PHPのカール:REST APIでPHPカール拡張機能を使用する方法
Mar 14, 2025 am 11:42 AM
PHPのカール:REST APIでPHPカール拡張機能を使用する方法
Mar 14, 2025 am 11:42 AM
PHPクライアントURL(CURL)拡張機能は、開発者にとって強力なツールであり、リモートサーバーやREST APIとのシームレスな対話を可能にします。尊敬されるマルチプロトコルファイル転送ライブラリであるLibcurlを活用することにより、PHP Curlは効率的なexecuを促進します
 PHPロギング:PHPログ分析のベストプラクティス
Mar 10, 2025 pm 02:32 PM
PHPロギング:PHPログ分析のベストプラクティス
Mar 10, 2025 pm 02:32 PM
PHPロギングは、Webアプリケーションの監視とデバッグ、および重要なイベント、エラー、ランタイムの動作をキャプチャするために不可欠です。システムのパフォーマンスに関する貴重な洞察を提供し、問題の特定に役立ち、より速いトラブルシューティングをサポートします
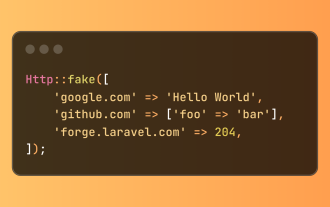 Laravelテストでの簡略化されたHTTP応答のモッキング
Mar 12, 2025 pm 05:09 PM
Laravelテストでの簡略化されたHTTP応答のモッキング
Mar 12, 2025 pm 05:09 PM
Laravelは簡潔なHTTP応答シミュレーション構文を提供し、HTTP相互作用テストを簡素化します。このアプローチは、テストシミュレーションをより直感的にしながら、コード冗長性を大幅に削減します。 基本的な実装は、さまざまな応答タイプのショートカットを提供します。 Illuminate \ support \ facades \ httpを使用します。 http :: fake([[ 'google.com' => 'hello world'、 'github.com' => ['foo' => 'bar']、 'forge.laravel.com' =>
 Codecanyonで12の最高のPHPチャットスクリプト
Mar 13, 2025 pm 12:08 PM
Codecanyonで12の最高のPHPチャットスクリプト
Mar 13, 2025 pm 12:08 PM
顧客の最も差し迫った問題にリアルタイムでインスタントソリューションを提供したいですか? ライブチャットを使用すると、顧客とのリアルタイムな会話を行い、すぐに問題を解決できます。それはあなたがあなたのカスタムにより速いサービスを提供することを可能にします
 PHPにおける後期静的結合の概念を説明します。
Mar 21, 2025 pm 01:33 PM
PHPにおける後期静的結合の概念を説明します。
Mar 21, 2025 pm 01:33 PM
記事では、PHP 5.3で導入されたPHPの後期静的結合(LSB)について説明し、より柔軟な継承を求める静的メソッドコールのランタイム解像度を可能にします。 LSBの実用的なアプリケーションと潜在的なパフォーマ
 フレームワークのカスタマイズ/拡張:カスタム機能を追加する方法。
Mar 28, 2025 pm 05:12 PM
フレームワークのカスタマイズ/拡張:カスタム機能を追加する方法。
Mar 28, 2025 pm 05:12 PM
この記事では、フレームワークにカスタム機能を追加し、アーキテクチャの理解、拡張ポイントの識別、統合とデバッグのベストプラクティスに焦点を当てています。







