PHP 配列の一般的な操作の概要_PHP チュートリアル
配列の合計
n 個の要素を含む整数配列 a が与えられた場合、a 内のすべての要素の合計を求めます。とても単純だと思うかもしれません。確かに単純ですが、なぜそう言う必要があるのでしょうか。まず、この質問では 1 行のコードを使用するだけで再帰を使用する必要があります。第二に、これは私が人生で初めて遭遇した面接の質問であり、特別な意味があります。
簡単に言うと、次の 2 つの状況があります:
配列の要素数が 0 の場合、合計は 0 になります。
配列内の要素の数が n の場合、最初に最初の n - 1 個の要素の合計を求め、次に a[n - 1] を加算します。
//配列 sum
int sum(int *a, int n)
{
return n == 0 ? : sum(a, n - 1) ) + a[n - 1];
}
配列の最大値と最小値を求める
n 個の要素を含む整数配列 a が与えられた場合、最大値と最小値を求めます。
従来のアプローチは、一度走査してそれぞれ最大値と最小値を見つけることですが、ここで説明するのは分割統治法 (Divide and Coquer) で、配列を左右の部分に分割し、まず左半分の最大値と最小値を求め、次に右半分の最大値と最小値を求め、それらを組み合わせて全体の最大値と最小値を求めます。これは再帰的なプロセスであり、分割された区間に要素が 1 つまたは 2 つだけ残るまで、分割された左右の部分に対してこのプロセスが繰り返されます。
// 配列の最大値と最小値を検索します。戻り値は maxValue と minValue です
void MaxandMin(int *a, int l, int r, int& maxValue, int& minValue )
{
if(l == r) // l と r の間に要素は 1 つだけあります
{
maxValue = a[l] ;
minValue = a[l] ;
}
if(l + 1 == r) // l と r の間に要素は 2 つだけです
{
if(a[l] >= a[r])
{
maxValue = a[l] ;
minValue = a[r] ;
else
{
maxValue = a[l]
}
int m = (l + r) ; ; // 中間点を求める
int lmax // 左半分の最大値
int lmin // 左半分の最小値
MaxandMin(a, l, m, lmax, lmin);左半分
int rmax; // 右半分の最大値
int rmin // 右半分の最小値
MaxandMin(a, m + 1, r, rmax, rmin);右半分
maxValue = max( lmax, rmax); //合計の最大値
minValue = min(lmin, rmin) //合計の最小値
}
次の最大値と 2 番目の最大値を求めます。配列
n 個の要素を含む配列を指定した整数配列で、その最大値と 2 番目の最大値を見つけます。
このアイデアは前の質問と似ていますが、分割統治法も使用しています。詳細は省略します。コードを見てください:
コードをコピーします
コードは次のとおりです:
else if(左 + 1 == 右)
{
最大 = a[左] >左] : a[右] ;
秒 = a [左] < a[左] : a[右]
}
int 中央 = 左 + (右 - 左) / 2 ;
int leftmin ;
int rightmin(a、mid + 1、rightmax、rightmin);
max = leftmax > leftmax : rightmax ;
Second = leftmax < rightmax : rightmax ;
配列が与えられた場合n 個の整数要素のうち 1 つの要素が n / 2 より多く出現し、この要素を見つけます。百度の面接質問だそうです。
現在の値と現在の値のカウンターを設定し、現在の値を配列の最初の要素に初期化します。カウンター値は 1 です。次に、走査された値 a[ ごとに 2 番目の要素から開始して配列全体を走査します。私]。
a[i]==currentValue の場合、カウンター値は 1 増加します。
a[i] != currentValue の場合、カウンター値は 1 減分されます。カウンター値が 0 未満の場合、現在の値は a[i] に更新され、カウンター値は 1 にリセットされます。
コードをコピーします
コードは次のとおりです:
//配列内で半分以上出現する要素を検索します
int Find(int* a, int n)
int curValue = a[0];
int カウント = 1;
for (int i = 1; i
もう 1 つの方法は、最初に配列をソートしてから中央の要素を取得することです。要素の数が半分を超える場合、その要素は配列のソート後に配列の中央の位置を占める必要があるからです。
配列内の要素間の最短距離を見つける
n 個の要素を含む整数配列が与えられた場合、abs(x - y) の値を最小にする配列内の 2 つの要素 x と y を見つけます。
まず配列をソートし、次にそれを 1 回走査します:
int Compare(const void* a, const void* b)
{
return * (int*) a - *(int*)b ;
void MinimumDistance(int* a, int n)
{
// 並べ替え
qsort(a, n, sizeof(int), Compare) ; int i ; // 数値 1 のインデックス
int minDistance = numeric_limits
for (int k = 0; k < n - 1; + +k)
{
if (a[k + 1] - a[k] < minDistance)
{
minDistance = a[k + 1] - a[k] ; = a[k + 1] ;
cout <
else// a[i] > j]
+ +j ;
}
}
たとえば、a には n 個の要素があるため、a の任意の要素に対して二分探索を実行します。 b. バイナリ検索にはログインが必要です。したがって、すべての同じ要素を見つける時間計算量は O(nlogn) です。
また、上記の方法では、bの二分探索を行っているだけなので、bが順番にあればaが順番にあるかどうかは関係ありません。 a も順序付けされている場合、上記の方法を使用すると少し遅くなります。 b の a の要素の位置が k の場合、 b の a の次の要素の位置は k の右側になければならないためです。したがって、今回の検索スペースは、全体をまだ検索するのではなく、最後の検索結果に基づいて絞り込むことができます。 b.つまり、a と b の両方が順序付けされている場合、コードを次のように変更して、最後の検索中の b 内の要素の位置を次の検索の開始点として記録できます。
3 つの配列の共通要素を見つける
n 個の要素を含む 3 つの整数配列 a、b、c が与えられた場合、それらの最小の共通要素を見つけます。
3 つの配列がすべて順序付けされている場合は、3 つの配列の先頭を指すように 3 つのポインターを設定し、共通の要素が見つかるまで 3 つのポインターが指す値の比較に基づいてポインターを移動できます。 。
コードをコピー
コードは次のとおりです:
// 3 つの配列の共通要素 - 最小のもののみを検索します
void FindCommonElements(int a[], int b[], int c[], int x, int y, int z)
{
for(int i = 0, j = 0, k = 0; i {
if(a[i ] < ; b[j])
{
i++ ;
}

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7476
7476
 15
15
 1377
1377
 52
52
 77
77
 11
11
 19
19
 31
31
 Ubuntu および Debian 用の PHP 8.4 インストールおよびアップグレード ガイド
Dec 24, 2024 pm 04:42 PM
Ubuntu および Debian 用の PHP 8.4 インストールおよびアップグレード ガイド
Dec 24, 2024 pm 04:42 PM
PHP 8.4 では、いくつかの新機能、セキュリティの改善、パフォーマンスの改善が行われ、かなりの量の機能の非推奨と削除が行われています。 このガイドでは、Ubuntu、Debian、またはその派生版に PHP 8.4 をインストールする方法、または PHP 8.4 にアップグレードする方法について説明します。
 CakePHP について話し合う
Sep 10, 2024 pm 05:28 PM
CakePHP について話し合う
Sep 10, 2024 pm 05:28 PM
CakePHP は、PHP 用のオープンソース フレームワークです。これは、アプリケーションの開発、展開、保守をより簡単にすることを目的としています。 CakePHP は、強力かつ理解しやすい MVC のようなアーキテクチャに基づいています。モデル、ビュー、コントローラー
 CakePHP ファイルのアップロード
Sep 10, 2024 pm 05:27 PM
CakePHP ファイルのアップロード
Sep 10, 2024 pm 05:27 PM
ファイルのアップロードを行うには、フォーム ヘルパーを使用します。ここではファイルアップロードの例を示します。
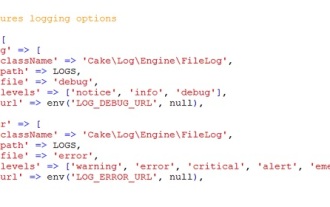 CakePHP のロギング
Sep 10, 2024 pm 05:26 PM
CakePHP のロギング
Sep 10, 2024 pm 05:26 PM
CakePHP へのログインは非常に簡単な作業です。使用する関数は 1 つだけです。 cronjob などのバックグラウンド プロセスのエラー、例外、ユーザー アクティビティ、ユーザーが実行したアクションをログに記録できます。 CakePHP でのデータのログ記録は簡単です。 log()関数が提供されています
 PHP 開発用に Visual Studio Code (VS Code) をセットアップする方法
Dec 20, 2024 am 11:31 AM
PHP 開発用に Visual Studio Code (VS Code) をセットアップする方法
Dec 20, 2024 am 11:31 AM
Visual Studio Code (VS Code とも呼ばれる) は、すべての主要なオペレーティング システムで利用できる無料のソース コード エディター (統合開発環境 (IDE)) です。 多くのプログラミング言語の拡張機能の大規模なコレクションを備えた VS Code は、
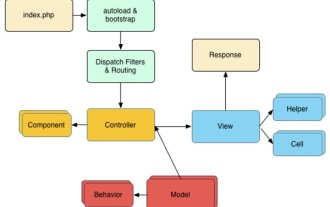 CakePHP クイックガイド
Sep 10, 2024 pm 05:27 PM
CakePHP クイックガイド
Sep 10, 2024 pm 05:27 PM
CakePHP はオープンソースの MVC フレームワークです。これにより、アプリケーションの開発、展開、保守がはるかに簡単になります。 CakePHP には、最も一般的なタスクの過負荷を軽減するためのライブラリが多数あります。