無限分類アルゴリズムに関するいくつかの記事 ページ 1/5_PHP チュートリアル
http://dev.mysql.com/tech-resources/articles/hierarchical-data.html
Introduction
Most users at one time or another have dealt with hierarchical data in a SQL database and no doubt learned that the management of hierarchical data is not what a relational database is intended for. The tables of a relational database are not hierarchical (like XML), but are simply a flat list. Hierarchical data has a parent-child relationship that is not naturally represented in a relational database table.
For our purposes, hierarchical data is a collection of data where each item has a single parent and zero or more children (with the exception of the root item, which has no parent). Hierarchical data can be found in a variety of database applications, including forum and mailing list threads, business organization charts, content management categories, and product categories. For our purposes we will use the following product category hierarchy from an fictional electronics store:

These categories form a hierarchy in much the same way as the other examples cited above. In this article we will examine two models for dealing with hierarchical data in MySQL, starting with the traditional adjacency list model.
The Adjacency List Model
Typically the example categories shown above will be stored in a table like the following (I'm including full CREATE and INSERT statements so you can follow along):
CREATE TABLE category( category_id INT AUTO_INCREMENT PRIMARY KEY, name VARCHAR(20) NOT NULL, parent INT DEFAULT NULL); INSERT INTO category VALUES(1,'ELECTRONICS',NULL),(2,'TELEVISIONS',1),(3,'TUBE',2), (4,'LCD',2),(5,'PLASMA',2),(6,'PORTABLE ELECTRONICS',1), (7,'MP3 PLAYERS',6),(8,'FLASH',7), (9,'CD PLAYERS',6),(10,'2 WAY RADIOS',6); SELECT * FROM category ORDER BY category_id; +-------------+----------------------+--------+ | category_id | name | parent | +-------------+----------------------+--------+ | 1 | ELECTRONICS | NULL | | 2 | TELEVISIONS | 1 | | 3 | TUBE | 2 | | 4 | LCD | 2 | | 5 | PLASMA | 2 | | 6 | PORTABLE ELECTRONICS | 1 | | 7 | MP3 PLAYERS | 6 | | 8 | FLASH | 7 | | 9 | CD PLAYERS | 6 | | 10 | 2 WAY RADIOS | 6 | +-------------+----------------------+--------+ 10 rows in set (0.00 sec)
In the adjacency list model, each item in the table contains a pointer to its parent. The topmost element, in this case electronics, has a NULL value for its parent. The adjacency list model has the advantage of being quite simple, it is easy to see that FLASH is a child of mp3 players, which is a child of portable electronics, which is a child of electronics. While the adjacency list model can be dealt with fairly easily in client-side code, working with the model can be more problematic in pure SQL.
Retrieving a Full Tree
The first common task when dealing with hierarchical data is the display of the entire tree, usually with some form of indentation. The most common way of doing this is in pure SQL is through the use of a self-join:
SELECT t1.name AS lev1, t2.name as lev2, t3.name as lev3, t4.name as lev4 FROM category AS t1 LEFT JOIN category AS t2 ON t2.parent = t1.category_id LEFT JOIN category AS t3 ON t3.parent = t2.category_id LEFT JOIN category AS t4 ON t4.parent = t3.category_id WHERE t1.name = 'ELECTRONICS'; +-------------+----------------------+--------------+-------+ | lev1 | lev2 | lev3 | lev4 | +-------------+----------------------+--------------+-------+ | ELECTRONICS | TELEVISIONS | TUBE | NULL | | ELECTRONICS | TELEVISIONS | LCD | NULL | | ELECTRONICS | TELEVISIONS | PLASMA | NULL | | ELECTRONICS | PORTABLE ELECTRONICS | MP3 PLAYERS | FLASH | | ELECTRONICS | PORTABLE ELECTRONICS | CD PLAYERS | NULL | | ELECTRONICS | PORTABLE ELECTRONICS | 2 WAY RADIOS | NULL | +-------------+----------------------+--------------+-------+ 6 rows in set (0.00 sec)
Finding all the Leaf Nodes
We can find all the leaf nodes in our tree (those with no children) by using a LEFT JOIN query:
SELECT t1.name FROM category AS t1 LEFT JOIN category as t2 ON t1.category_id = t2.parent WHERE t2.category_id IS NULL; +--------------+ | name | +--------------+ | TUBE | | LCD | | PLASMA | | FLASH | | CD PLAYERS | | 2 WAY RADIOS | +--------------+
Retrieving a Single Path
The self-join also allows us to see the full path through our hierarchies:
SELECT t1.name AS lev1, t2.name as lev2, t3.name as lev3, t4.name as lev4 FROM category AS t1 LEFT JOIN category AS t2 ON t2.parent = t1.category_id LEFT JOIN category AS t3 ON t3.parent = t2.category_id LEFT JOIN category AS t4 ON t4.parent = t3.category_id WHERE t1.name = 'ELECTRONICS' AND t4.name = 'FLASH'; +-------------+----------------------+-------------+-------+ | lev1 | lev2 | lev3 | lev4 | +-------------+----------------------+-------------+-------+ | ELECTRONICS | PORTABLE ELECTRONICS | MP3 PLAYERS | FLASH | +-------------+----------------------+-------------+-------+ 1 row in set (0.01 sec)
The main limitation of such an approach is that you need one self-join for every level in the hierarchy, and performance will naturally degrade with each level added as the joining grows in complexity.
Limitations of the Adjacency List Model
Working with the adjacency list model in pure SQL can be difficult at best. Before being able to see the full path of a category we have to know the level at which it resides. In addition, special care must be taken when deleting nodes because of the potential for orphaning an entire sub-tree in the process (delete the portable electronics category and all of its children are orphaned). Some of these limitations can be addressed through the use of client-side code or stored procedures. With a procedural language we can start at the bottom of the tree and iterate upwards to return the full tree or a single path. We can also use procedural programming to delete nodes without orphaning entire sub-trees by promoting one child element and re-ordering the remaining children to point to the new parent.
The Nested Set Model
What I would like to focus on in this article is a different approach, commonly referred to as the Nested Set Model. In the Nested Set Model, we can look at our hierarchy in a new way, not as nodes and lines, but as nested containers. Try picturing our electronics categories this way:

Notice how our hierarchy is still maintained, as parent categories envelop their children.We represent this form of hierarchy in a table through the use of left and right values to represent the nesting of our nodes:
CREATE TABLE nested_category ( category_id INT AUTO_INCREMENT PRIMARY KEY, name VARCHAR(20) NOT NULL, lft INT NOT NULL, rgt INT NOT NULL ); INSERT INTO nested_category VALUES(1,'ELECTRONICS',1,20),(2,'TELEVISIONS',2,9),(3,'TUBE',3,4), (4,'LCD',5,6),(5,'PLASMA',7,8),(6,'PORTABLE ELECTRONICS',10,19), (7,'MP3 PLAYERS',11,14),(8,'FLASH',12,13), (9,'CD PLAYERS',15,16),(10,'2 WAY RADIOS',17,18); SELECT * FROM nested_category ORDER BY category_id; +-------------+----------------------+-----+-----+ | category_id | name | lft | rgt | +-------------+----------------------+-----+-----+ | 1 | ELECTRONICS | 1 | 20 | | 2 | TELEVISIONS | 2 | 9 | | 3 | TUBE | 3 | 4 | | 4 | LCD | 5 | 6 | | 5 | PLASMA | 7 | 8 | | 6 | PORTABLE ELECTRONICS | 10 | 19 | | 7 | MP3 PLAYERS | 11 | 14 | | 8 | FLASH | 12 | 13 | | 9 | CD PLAYERS | 15 | 16 | | 10 | 2 WAY RADIOS | 17 | 18 | +-------------+----------------------+-----+-----+
We use lft and rgt because left and right are reserved words in MySQL, see http://dev.mysql.com/doc/mysql/en/reserved-words.html for the full list of reserved words.
So how do we determine left and right values? We start numbering at the leftmost side of the outer node and continue to the right:

This design can be applied to a typical tree as well:

When working with a tree, we work from left to right, one layer at a time, descending to each node's children before assigning a right-hand number and moving on to the right. This approach is called the modified preorder tree traversal algorithm.
Retrieving a Full Tree
We can retrieve the full tree through the use of a self-join that links parents with nodes on the basis that a node's lft value will always appear between its parent's lft and rgt values:
SELECT node.name FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt AND parent.name = 'ELECTRONICS' ORDER BY node.lft; +----------------------+ | name | +----------------------+ | ELECTRONICS | | TELEVISIONS | | TUBE | | LCD | | PLASMA | | PORTABLE ELECTRONICS | | MP3 PLAYERS | | FLASH | | CD PLAYERS | | 2 WAY RADIOS | +----------------------+
Unlike our previous examples with the adjacency list model, this query will work regardless of the depth of the tree. We do not concern ourselves with the rgt value of the node in our BETWEEN clause because the rgt value will always fall within the same parent as the lft values.
Finding all the Leaf Nodes
Finding all leaf nodes in the nested set model even simpler than the LEFT JOIN method used in the adjacency list model. If you look at the nested_category table, you may notice that the lft and rgt values for leaf nodes are consecutive numbers. To find the leaf nodes, we look for nodes where rgt = lft + 1:
SELECT name FROM nested_category WHERE rgt = lft + 1; +--------------+ | name | +--------------+ | TUBE | | LCD | | PLASMA | | FLASH | | CD PLAYERS | | 2 WAY RADIOS | +--------------+
Retrieving a Single Path
With the nested set model, we can retrieve a single path without having multiple self-joins:
SELECT parent.name FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt AND node.name = 'FLASH' ORDER BY node.lft; +----------------------+ | name | +----------------------+ | ELECTRONICS | | PORTABLE ELECTRONICS | | MP3 PLAYERS | | FLASH | +----------------------+
Finding the Depth of the Nodes
We have already looked at how to show the entire tree, but what if we want to also show the depth of each node in the tree, to better identify how each node fits in the hierarchy? This can be done by adding a COUNT function and a GROUP BY clause to our existing query for showing the entire tree:
SELECT node.name, (COUNT(parent.name) - 1) AS depth FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt GROUP BY node.name ORDER BY node.lft; +----------------------+-------+ | name | depth | +----------------------+-------+ | ELECTRONICS | 0 | | TELEVISIONS | 1 | | TUBE | 2 | | LCD | 2 | | PLASMA | 2 | | PORTABLE ELECTRONICS | 1 | | MP3 PLAYERS | 2 | | FLASH | 3 | | CD PLAYERS | 2 | | 2 WAY RADIOS | 2 | +----------------------+-------+
We can use the depth value to indent our category names with the CONCAT and REPEAT string functions:
SELECT CONCAT( REPEAT(' ', COUNT(parent.name) - 1), node.name) AS name
FROM nested_category AS node,
nested_category AS parent
WHERE node.lft BETWEEN parent.lft AND parent.rgt
GROUP BY node.name
ORDER BY node.lft;
+-----------------------+
| name |
+-----------------------+
| ELECTRONICS |
| TELEVISIONS |
| TUBE |
| LCD |
| PLASMA |
| PORTABLE ELECTRONICS |
| MP3 PLAYERS |
| FLASH |
| CD PLAYERS |
| 2 WAY RADIOS |
+-----------------------+
Of course, in a client-side application you will be more likely to use the depth value directly to display your hierarchy. Web developers could loop through the tree, adding
andDepth of a Sub-Tree
When we need depth information for a sub-tree, we cannot limit either the node or parent tables in our self-join because it will corrupt our results. Instead, we add a third self-join, along with a sub-query to determine the depth that will be the new starting point for our sub-tree:
SELECT node.name, (COUNT(parent.name) - (sub_tree.depth + 1)) AS depth FROM nested_category AS node, nested_category AS parent, nested_category AS sub_parent, ( SELECT node.name, (COUNT(parent.name) - 1) AS depth FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt AND node.name = 'PORTABLE ELECTRONICS' GROUP BY node.name ORDER BY node.lft )AS sub_tree WHERE node.lft BETWEEN parent.lft AND parent.rgt AND node.lft BETWEEN sub_parent.lft AND sub_parent.rgt AND sub_parent.name = sub_tree.name GROUP BY node.name ORDER BY node.lft; +----------------------+-------+ | name | depth | +----------------------+-------+ | PORTABLE ELECTRONICS | 0 | | MP3 PLAYERS | 1 | | FLASH | 2 | | CD PLAYERS | 1 | | 2 WAY RADIOS | 1 | +----------------------+-------+
This function can be used with any node name, including the root node. The depth values are always relative to the named node.
Find the Immediate Subordinates of a Node
Imagine you are showing a category of electronics products on a retailer web site. When a user clicks on a category, you would want to show the products of that category, as well as list its immediate sub-categories, but not the entire tree of categories beneath it. For this, we need to show the node and its immediate sub-nodes, but no further down the tree. For example, when showing the PORTABLE ELECTRONICS category, we will want to show MP3 PLAYERS, CD PLAYERS, and 2 WAY RADIOS, but not FLASH.
This can be easily accomplished by adding a HAVING clause to our previous query:
SELECT node.name, (COUNT(parent.name) - (sub_tree.depth + 1)) AS depth FROM nested_category AS node, nested_category AS parent, nested_category AS sub_parent, ( SELECT node.name, (COUNT(parent.name) - 1) AS depth FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt AND node.name = 'PORTABLE ELECTRONICS' GROUP BY node.name ORDER BY node.lft )AS sub_tree WHERE node.lft BETWEEN parent.lft AND parent.rgt AND node.lft BETWEEN sub_parent.lft AND sub_parent.rgt AND sub_parent.name = sub_tree.name GROUP BY node.name HAVING depth <= 1 ORDER BY node.lft; +----------------------+-------+ | name | depth | +----------------------+-------+ | PORTABLE ELECTRONICS | 0 | | MP3 PLAYERS | 1 | | CD PLAYERS | 1 | | 2 WAY RADIOS | 1 | +----------------------+-------+
If you do not wish to show the parent node, change the HAVING depth <= 1 line to HAVING depth = 1.
Aggregate Functions in a Nested Set
Let's add a table of products that we can use to demonstrate aggregate functions with:
CREATE TABLE product(
product_id INT AUTO_INCREMENT PRIMARY KEY,
name VARCHAR(40),
category_id INT NOT NULL
);
INSERT INTO product(name, category_id) VALUES('20" TV',3),('36" TV',3),
('Super-LCD 42"',4),('Ultra-Plasma 62"',5),('Value Plasma 38"',5),
('Power-MP3 5gb',7),('Super-Player 1gb',8),('Porta CD',9),('CD To go!',9),
('Family Talk 360',10);
SELECT * FROM product;
+------------+-------------------+-------------+
| product_id | name | category_id |
+------------+-------------------+-------------+
| 1 | 20" TV | 3 |
| 2 | 36" TV | 3 |
| 3 | Super-LCD 42" | 4 |
| 4 | Ultra-Plasma 62" | 5 |
| 5 | Value Plasma 38" | 5 |
| 6 | Power-MP3 128mb | 7 |
| 7 | Super-Shuffle 1gb | 8 |
| 8 | Porta CD | 9 |
| 9 | CD To go! | 9 |
| 10 | Family Talk 360 | 10 |
+------------+-------------------+-------------+
Now let's produce a query that can retrieve our category tree, along with a product count for each category:
SELECT parent.name, COUNT(product.name) FROM nested_category AS node , nested_category AS parent, product WHERE node.lft BETWEEN parent.lft AND parent.rgt AND node.category_id = product.category_id GROUP BY parent.name ORDER BY node.lft; +----------------------+---------------------+ | name | COUNT(product.name) | +----------------------+---------------------+ | ELECTRONICS | 10 | | TELEVISIONS | 5 | | TUBE | 2 | | LCD | 1 | | PLASMA | 2 | | PORTABLE ELECTRONICS | 5 | | MP3 PLAYERS | 2 | | FLASH | 1 | | CD PLAYERS | 2 | | 2 WAY RADIOS | 1 | +----------------------+---------------------+
This is our typical whole tree query with a COUNT and GROUP BY added, along with a reference to the product table and a join between the node and product table in the WHERE clause. As you can see, there is a count for each category and the count of subcategories is reflected in the parent categories.
Adding New Nodes
Now that we have learned how to query our tree, we should take a look at how to update our tree by adding a new node. Let's look at our nested set diagram again:

If we wanted to add a new node between the TELEVISIONS and PORTABLE ELECTRONICS nodes, the new node would have lft and rgt values of 10 and 11, and all nodes to its right would have their lft and rgt values increased by two. We would then add the new node with the appropriate lft and rgt values. While this can be done with a stored procedure in MySQL 5, I will assume for the moment that most readers are using 4.1, as it is the latest stable version, and I will isolate my queries with a LOCK TABLES statement instead:
LOCK TABLE nested_category WRITE;
SELECT @myRight := rgt FROM nested_category
WHERE name = 'TELEVISIONS';
UPDATE nested_category SET rgt = rgt + 2 WHERE rgt > @myRight;
UPDATE nested_category SET lft = lft + 2 WHERE lft > @myRight;
INSERT INTO nested_category(name, lft, rgt) VALUES('GAME CONSOLES', @myRight + 1, @myRight + 2);
UNLOCK TABLES;
We can then check our nesting with our indented tree query:
SELECT CONCAT( REPEAT( ' ', (COUNT(parent.name) - 1) ), node.name) AS name
FROM nested_category AS node,
nested_category AS parent
WHERE node.lft BETWEEN parent.lft AND parent.rgt
GROUP BY node.name
ORDER BY node.lft;
+-----------------------+
| name |
+-----------------------+
| ELECTRONICS |
| TELEVISIONS |
| TUBE |
| LCD |
| PLASMA |
| GAME CONSOLES |
| PORTABLE ELECTRONICS |
| MP3 PLAYERS |
| FLASH |
| CD PLAYERS |
| 2 WAY RADIOS |
+-----------------------+
If we instead want to add a node as a child of a node that has no existing children, we need to modify our procedure slightly. Let's add a new FRS node below the 2 WAY RADIOS node:
LOCK TABLE nested_category WRITE;
SELECT @myLeft := lft FROM nested_category
WHERE name = '2 WAY RADIOS';
UPDATE nested_category SET rgt = rgt + 2 WHERE rgt > @myLeft;
UPDATE nested_category SET lft = lft + 2 WHERE lft > @myLeft;
INSERT INTO nested_category(name, lft, rgt) VALUES('FRS', @myLeft + 1, @myLeft + 2);
UNLOCK TABLES;
In this example we expand everything to the right of the left-hand number of our proud new parent node, then place the node to the right of the left-hand value. As you can see, our new node is now properly nested:
SELECT CONCAT( REPEAT( ' ', (COUNT(parent.name) - 1) ), node.name) AS name FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt GROUP BY node.name ORDER BY node.lft; +-----------------------+ | name | +-----------------------+ | ELECTRONICS | | TELEVISIONS | | TUBE | | LCD | | PLASMA | | GAME CONSOLES | | PORTABLE ELECTRONICS | | MP3 PLAYERS | | FLASH | | CD PLAYERS | | 2 WAY RADIOS | | FRS | +-----------------------+
Deleting Nodes
The last basic task involved in working with nested sets is the removal of nodes. The course of action you take when deleting a node depends on the node's position in the hierarchy; deleting leaf nodes is easier than deleting nodes with children because we have to handle the orphaned nodes.
When deleting a leaf node, the process if just the opposite of adding a new node, we delete the node and its width from every node to its right:
LOCK TABLE nested_category WRITE; SELECT @myLeft := lft, @myRight := rgt, @myWidth := rgt - lft + 1 FROM nested_category WHERE name = 'GAME CONSOLES'; DELETE FROM nested_category WHERE lft BETWEEN @myLeft AND @myRight; UPDATE nested_category SET rgt = rgt - @myWidth WHERE rgt > @myRight; UPDATE nested_category SET lft = lft - @myWidth WHERE lft > @myRight; UNLOCK TABLES;
And once again, we execute our indented tree query to confirm that our node has been deleted without corrupting the hierarchy:
SELECT CONCAT( REPEAT( ' ', (COUNT(parent.name) - 1) ), node.name) AS name FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt GROUP BY node.name ORDER BY node.lft; +-----------------------+ | name | +-----------------------+ | ELECTRONICS | | TELEVISIONS | | TUBE | | LCD | | PLASMA | | PORTABLE ELECTRONICS | | MP3 PLAYERS | | FLASH | | CD PLAYERS | | 2 WAY RADIOS | | FRS | +-----------------------+
This approach works equally well to delete a node and all its children:
LOCK TABLE nested_category WRITE; SELECT @myLeft := lft, @myRight := rgt, @myWidth := rgt - lft + 1 FROM nested_category WHERE name = 'MP3 PLAYERS'; DELETE FROM nested_category WHERE lft BETWEEN @myLeft AND @myRight; UPDATE nested_category SET rgt = rgt - @myWidth WHERE rgt > @myRight; UPDATE nested_category SET lft = lft - @myWidth WHERE lft > @myRight; UNLOCK TABLES;
And once again, we query to see that we have successfully deleted an entire sub-tree:
SELECT CONCAT( REPEAT( ' ', (COUNT(parent.name) - 1) ), node.name) AS name FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt GROUP BY node.name ORDER BY node.lft; +-----------------------+ | name | +-----------------------+ | ELECTRONICS | | TELEVISIONS | | TUBE | | LCD | | PLASMA | | PORTABLE ELECTRONICS | | CD PLAYERS | | 2 WAY RADIOS | | FRS | +-----------------------+
The other scenario we have to deal with is the deletion of a parent node but not the children. In some cases you may wish to just change the name to a placeholder until a replacement is presented, such as when a supervisor is fired. In other cases, the child nodes should all be moved up to the level of the deleted parent:
LOCK TABLE nested_category WRITE; SELECT @myLeft := lft, @myRight := rgt, @myWidth := rgt - lft + 1 FROM nested_category WHERE name = 'PORTABLE ELECTRONICS'; DELETE FROM nested_category WHERE lft = @myLeft; UPDATE nested_category SET rgt = rgt - 1, lft = lft - 1 WHERE lft BETWEEN @myLeft AND @myRight; UPDATE nested_category SET rgt = rgt - 2 WHERE rgt > @myRight; UPDATE nested_category SET lft = lft - 2 WHERE lft > @myRight; UNLOCK TABLES;
In this case we subtract two from all elements to the right of the node (since without children it would have a width of two), and one from the nodes that are its children (to close the gap created by the loss of the parent's left value). Once again, we can confirm our elements have been promoted:
SELECT CONCAT( REPEAT( ' ', (COUNT(parent.name) - 1) ), node.name) AS name FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt GROUP BY node.name ORDER BY node.lft; +---------------+ | name | +---------------+ | ELECTRONICS | | TELEVISIONS | | TUBE | | LCD | | PLASMA | | CD PLAYERS | | 2 WAY RADIOS | | FRS | +---------------+
Other scenarios when deleting nodes would include promoting one of the children to the parent position and moving the child nodes under a sibling of the parent node, but for the sake of space these scenarios will not be covered in this article.

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7762
7762
 15
15
 1644
1644
 14
14
 1399
1399
 52
52
 1293
1293
 25
25
 1234
1234
 29
29
 CLIP-BEVFormer: BEVFormer 構造を明示的に監視して、ロングテール検出パフォーマンスを向上させます。
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: BEVFormer 構造を明示的に監視して、ロングテール検出パフォーマンスを向上させます。
Mar 26, 2024 pm 12:41 PM
上記および筆者の個人的な理解: 現在、自動運転システム全体において、認識モジュールが重要な役割を果たしている。道路を走行する自動運転車は、認識モジュールを通じてのみ正確な認識結果を得ることができる。下流の規制および制御モジュール自動運転システムでは、タイムリーかつ正確な判断と行動決定が行われます。現在、自動運転機能を備えた自動車には通常、サラウンドビューカメラセンサー、ライダーセンサー、ミリ波レーダーセンサーなどのさまざまなデータ情報センサーが搭載されており、さまざまなモダリティで情報を収集して正確な認識タスクを実現しています。純粋な視覚に基づく BEV 認識アルゴリズムは、ハードウェア コストが低く導入が容易であるため、業界で好まれており、その出力結果はさまざまな下流タスクに簡単に適用できます。
 今すぐ Toutiao の記事を公開してお金を稼ぐにはどうすればよいですか?今すぐ Toutiao で記事を公開して収入を増やす方法!
Mar 15, 2024 pm 04:13 PM
今すぐ Toutiao の記事を公開してお金を稼ぐにはどうすればよいですか?今すぐ Toutiao で記事を公開して収入を増やす方法!
Mar 15, 2024 pm 04:13 PM
1. 今すぐ Toutiao の記事を公開してどうやってお金を稼ぐことができますか?今すぐ Toutiao で記事を公開して収入を増やす方法! 1. 基本的な権利と利益の有効化: オリジナルの記事は広告によって利益を得ることができますが、利益を得るにはビデオが横画面モードでオリジナルである必要があります。 2. ファン100人の権利を有効化:ファン数が100人以上に達すると、マイクロヘッドライン、オリジナルQ&A作成、Q&Aから利益を得ることができます。 3. オリジナル作品にこだわる: オリジナル作品には記事、小見出し、質問などが含まれ、300 ワード以上であることが求められます。違法に盗用された作品をオリジナル作品として出版した場合、クレジットポイントが減点され、利益も差し引かれますのでご注意ください。 4. 垂直性:専門分野の記事を書く場合、分野を超えて自由に記事を書くことができず、適切な推薦が得られず、専門性や洗練度が得られず、ファンもつきにくいそして読者たち。 5. 活動: 高活動、
 C++ での機械学習アルゴリズムの実装: 一般的な課題と解決策
Jun 03, 2024 pm 01:25 PM
C++ での機械学習アルゴリズムの実装: 一般的な課題と解決策
Jun 03, 2024 pm 01:25 PM
C++ の機械学習アルゴリズムが直面する一般的な課題には、メモリ管理、マルチスレッド、パフォーマンスの最適化、保守性などがあります。解決策には、スマート ポインター、最新のスレッド ライブラリ、SIMD 命令、サードパーティ ライブラリの使用、コーディング スタイル ガイドラインの遵守、自動化ツールの使用が含まれます。実践的な事例では、Eigen ライブラリを使用して線形回帰アルゴリズムを実装し、メモリを効果的に管理し、高性能の行列演算を使用する方法を示します。
 C++sort 関数の基礎となる原則とアルゴリズムの選択を調べる
Apr 02, 2024 pm 05:36 PM
C++sort 関数の基礎となる原則とアルゴリズムの選択を調べる
Apr 02, 2024 pm 05:36 PM
C++sort 関数の最下層はマージ ソートを使用し、その複雑さは O(nlogn) で、クイック ソート、ヒープ ソート、安定したソートなど、さまざまなソート アルゴリズムの選択肢を提供します。
 人工知能は犯罪を予測できるのか? CrimeGPT の機能を調べる
Mar 22, 2024 pm 10:10 PM
人工知能は犯罪を予測できるのか? CrimeGPT の機能を調べる
Mar 22, 2024 pm 10:10 PM
人工知能 (AI) と法執行機関の融合により、犯罪の予防と検出の新たな可能性が開かれます。人工知能の予測機能は、犯罪行為を予測するためにCrimeGPT (犯罪予測技術) などのシステムで広く使用されています。この記事では、犯罪予測における人工知能の可能性、その現在の応用、人工知能が直面する課題、およびこの技術の倫理的影響について考察します。人工知能と犯罪予測: 基本 CrimeGPT は、機械学習アルゴリズムを使用して大規模なデータセットを分析し、犯罪がいつどこで発生する可能性があるかを予測できるパターンを特定します。これらのデータセットには、過去の犯罪統計、人口統計情報、経済指標、気象パターンなどが含まれます。人間のアナリストが見逃す可能性のある傾向を特定することで、人工知能は法執行機関に力を与えることができます
 改良された検出アルゴリズム: 高解像度の光学式リモートセンシング画像でのターゲット検出用
Jun 06, 2024 pm 12:33 PM
改良された検出アルゴリズム: 高解像度の光学式リモートセンシング画像でのターゲット検出用
Jun 06, 2024 pm 12:33 PM
01 今後の概要 現時点では、検出効率と検出結果の適切なバランスを実現することが困難です。我々は、光学リモートセンシング画像におけるターゲット検出ネットワークの効果を向上させるために、多層特徴ピラミッド、マルチ検出ヘッド戦略、およびハイブリッドアテンションモジュールを使用して、高解像度光学リモートセンシング画像におけるターゲット検出のための強化されたYOLOv5アルゴリズムを開発しました。 SIMD データセットによると、新しいアルゴリズムの mAP は YOLOv5 より 2.2%、YOLOX より 8.48% 優れており、検出結果と速度のバランスがより優れています。 02 背景と動機 リモート センシング技術の急速な発展に伴い、航空機、自動車、建物など、地表上の多くの物体を記述するために高解像度の光学式リモート センシング画像が使用されています。リモートセンシング画像の判読における物体検出
 58 ポートレート プラットフォームの構築におけるアルゴリズムの適用
May 09, 2024 am 09:01 AM
58 ポートレート プラットフォームの構築におけるアルゴリズムの適用
May 09, 2024 am 09:01 AM
1. 58 Portraits プラットフォーム構築の背景 まず、58 Portraits プラットフォーム構築の背景についてお話ししたいと思います。 1. 従来のプロファイリング プラットフォームの従来の考え方ではもはや十分ではありません。ユーザー プロファイリング プラットフォームを構築するには、複数のビジネス分野からのデータを統合して、ユーザーの行動や関心を理解するためのデータ マイニングも必要です。最後に、ユーザー プロファイル データを効率的に保存、クエリ、共有し、プロファイル サービスを提供するためのデータ プラットフォーム機能も必要です。自社構築のビジネス プロファイリング プラットフォームとミドルオフィス プロファイリング プラットフォームの主な違いは、自社構築のプロファイリング プラットフォームは単一のビジネス ラインにサービスを提供し、オンデマンドでカスタマイズできることです。ミッドオフィス プラットフォームは複数のビジネス ラインにサービスを提供し、複雑な機能を備えていることです。モデリングを提供し、より一般的な機能を提供します。 2.58 中間プラットフォームのポートレート構築の背景のユーザーのポートレート 58
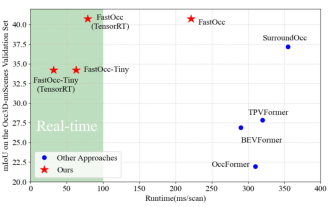 SOTA をリアルタイムで追加すると、大幅に増加します。 FastOcc: より高速な推論と展開に適した Occ アルゴリズムが登場しました。
Mar 14, 2024 pm 11:50 PM
SOTA をリアルタイムで追加すると、大幅に増加します。 FastOcc: より高速な推論と展開に適した Occ アルゴリズムが登場しました。
Mar 14, 2024 pm 11:50 PM
上記と著者の個人的な理解は、自動運転システムにおいて、認識タスクは自動運転システム全体の重要な要素であるということです。認識タスクの主な目的は、自動運転車が道路を走行する車両、路側の歩行者、運転中に遭遇する障害物、道路上の交通標識などの周囲の環境要素を理解して認識できるようにすることで、それによって下流のシステムを支援できるようにすることです。モジュール 正しく合理的な決定と行動を行います。自動運転機能を備えた車両には、通常、サラウンドビューカメラセンサー、ライダーセンサー、ミリ波レーダーセンサーなど、さまざまな種類の情報収集センサーが装備されており、自動運転車が正確に認識し、認識できるようにします。周囲の環境要素を理解することで、自動運転車が自動運転中に正しい判断を下せるようになります。頭




