最大サブシーケンスとアルゴリズムの分析
問題の説明: n 個の整数シーケンス {a1, a2,...,an} が与えられた場合、関数 f(i,j)=max{0,Σak}(k: i から j まで連続);
問題は、連続する部分系列の合計の最大値を見つけることです。最大値が負の数の場合は、8 つの数列 {-1,2,-3,4,-2 など) をとります。 ,5, -8,3}、Namo の最大部分列合計は 4+(-2)+5=7 です。
この問題には複雑さの異なる 4 つのアルゴリズムがあります。アルゴリズム 1 から 4 の時間計算量は O( n 3),O(n2),O(nlogn),O(n);
アルゴリズム 1:
最も直接的な方法は、すべての状況をリストし、その後の順序を設定できます。左端 i と右端 j を計算し、レイヤーを使用して a[i] から a[j] までの合計を計算します。
//最大のサブカラムと網羅的なメソッド
#include
namespace を使用std;
int Find_Maxsun (int*a, int n);
int main(){
int n, i;
int a[100];
cin >>
cout << 「 << ; n << "Number:" << endl;
for (i = 0; i < n; i++)
cin >> a[i];
cout<< ;Find_Maxsun(a, n) << endl;
return 0;
}
int Find_Maxsun(int*a, int n){
int MaxSun = 0, i, j, k;
int NowSum;
for ( i = 0; i < n; i++) /*部分列の左端*/
for (j = 0; j < n; j++){ /*部分列の右端*/
NowSum = 0;
for ( k = i; k < = j++)
NowSum += a[k]; /* a[i] から a[j] までのシーケンス */
if (NowSum>MaxSun)
MaxSun; Update result*/
}
return MaxSun;
}
明らかに、総当たり法では 3 つの for ループが使用され、アルゴリズムの時間計算量は もちろん最も愚かなアルゴリズムですが、データは非常に大きいので、たとえ死ぬほど計算しなければならないとしても、j が追加されるたびにサブカラムの合計を再度計算する必要があることがわかります。 j-1の結果は?つまり、j-1 の結果を保存します。ステップ j の結果を計算するときは、ステップ j-1 に基づいて a[j] を加算するだけで済みます。したがって、アルゴリズム 2 が存在します。
アルゴリズム 2:
#include
int Find_Maxsun2(int*a, int n);
int main(){
int n, i;
int a[100];
cin >>
cout <<「<
cout << Find_Maxsun2(a, n) << endl;
return 0;
}
int Find_Maxsun2(int*a, int n) , j, NewSum = 0, MaxSum= 0;
for (i = 0; i
for (j = i; j < n; j++){ /*j は系列の右端点です*/
NewSum += a[j] /* j-1 条件で毎回 NewSum を更新します*/
if (NewSum>MaxSum) /* Update MaxSum*/
MaxSum = NewSum;
}
}
return MaxSum;
}
このアルゴリズムは 1 よりも賢く、アルゴリズムの複雑さは O(n
2
アルゴリズム 3:
アルゴリズム 3 は分割統治のアイデアを使用します。基本的な考え方は自明です。最初に分割してから征服し、問題を小さな問題に分解し、次に解決する小さな問題を合計します。元のシーケンスを 1 つに分割し、最大のサブシーケンスを左側、右側、または境界を越えて配置します。 基本的な考え方は次のとおりです: ステップ 1: 元のシーケンスを 2 つに分割します。左のシーケンスと右のシーケンス。 ステップ 2: サブシーケンス S left と S right を再帰的に見つけます。 パート 3: 中心線から両側に向かってスキャンして、中心線と S を横切る最大のサブシーケンスを見つけます。 ステップ 4: S=max{S left, S middle, S right} を求める コードは次のように実装されます。#include
名前空間 std を使用;
int Find_MaxSum3(int*a,int low,int high);
int Max(int a,int b,int c);
int main(){
int n, i;
int a[100];
cin >> n;
cout cin >> a[i];
cout return 0;
}
int Find_MaxSum3(int*a,int low,int high){
int MaxSum = 0, MidSum, LeftSum, RightSum,i;
MidSum = 0;
if (low == high){ /*終了条件recursion* /
if (a[low] > 0)
return a[low];
else
return 0;
}
int mid = (low + high) // 分の中間点を見つける
; LeftSum = Find_MaxSum3 (a, low, middle); /*左のシーケンスの最大合計を再帰的に求めます*/
RightSum = Find_MaxSum3(a, mid + 1, high); /*右のシーケンスの最大のサブシーケンスの合計を再帰的に求めます*/
/*次に、中間の境界を越えるシーケンスの最大合計を見つけることができます*/
int NewLeft = 0,Max_BorderLeft=0, NewRight = 0,Max_BorderRight=0;
for (i = Mid; i >= low; i --){ /*左をスキャンして最大合計を見つけます*/
NewLeft += a[i];
if (NewLeft > Max_BorderLeft)
Max_BorderLeft = NewLeft;
}
for (i = mid + 1; i NewRight+=a[i];
if (NewRight >= Max_BorderRight)
Max_BorderRight = NewRight;
}
MidSum = Max_BorderRight + Max_BorderLeft;
return Max(LeftSum, MidSum, RightSum) ; /*ルールの結果を返します*/
}
int Max(int a, int b, int c){ /*3 つの中で最大の数値を見つけます*/
if ( a>= b&&a >= c)
return a;
if (b >= a&&b >= c)
return b;
if (c >= b&&c>=a)
return c;
}
kT(n /2k)+kO(n) =2kT(1)+kO(n) (n=2k)=n+nlogn=O(nlogn);
このアルゴリズムは非常に優れていますが、最速のアルゴリズムではありません。 アルゴリズム 4: アルゴリズム 4 はオンライン処理と呼ばれます。これは、データが読み込まれるたびに、時間内に処理され、得られた結果が現在読み込まれているデータに当てはまります。つまり、アルゴリズムはどの位置でも正しい解を与えることができ、アルゴリズムは次のことを行うことができます。読みながら正しい解決策を見つけてください。 #include名前空間 std を使用;
int Find_MaxSum4(int*a, int n);
int main(){
int n, i;
int a[100];
cin >> ;
cout << "<
cout << Find_MaxSum4(a,n) << endl;
return 0;
}
int Find_MaxSum4(int*a, int n){
int i, NewSum = 0, MaxSum = 0;
for (i = 0; i
if (MaxSum
if (NewSum NewSum = 0;
}
return MaxSum;
}
以上、最大サブシーケンスとアルゴリズム解析を内容も含めて紹介しましたが、PHPチュートリアルに興味のある方の参考になれば幸いです。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7696
7696
 15
15
 1640
1640
 14
14
 1393
1393
 52
52
 1287
1287
 25
25
 1229
1229
 29
29
 Huawei GT3 ProとGT4の違いは何ですか?
Dec 29, 2023 pm 02:27 PM
Huawei GT3 ProとGT4の違いは何ですか?
Dec 29, 2023 pm 02:27 PM
多くのユーザーはスマートウォッチを選ぶときにファーウェイブランドを選択しますが、その中でもファーウェイ GT3pro と GT4 は非常に人気のある選択肢であり、多くのユーザーはファーウェイ GT3pro と GT4 の違いに興味を持っています。 Huawei GT3pro と GT4 の違いは何ですか? 1. 外観 GT4: 46mm と 41mm、材質はガラスミラー + ステンレススチールボディ + 高解像度ファイバーバックシェルです。 GT3pro: 46.6mm および 42.9mm、材質はサファイアガラス + チタンボディ/セラミックボディ + セラミックバックシェルです。 2. 健全な GT4: 最新の Huawei Truseen5.5+ アルゴリズムを使用すると、結果はより正確になります。 GT3pro: ECG 心電図と血管と安全性を追加
 C言語のreturnの使い方を詳しく解説
Oct 07, 2023 am 10:58 AM
C言語のreturnの使い方を詳しく解説
Oct 07, 2023 am 10:58 AM
C 言語における return の使い方は、 1. 戻り値の型が void の関数については、return 文を使用して関数の実行を早期に終了することができます; 2. 戻り値の型が void ではない関数については、 return ステートメントは、関数の実行を終了するためのものです。結果は呼び出し元に返されます。 3. 関数の実行を早期に終了します。関数内で return ステートメントを使用して、関数の実行を早期に終了することもできます。関数が値を返さない場合。
 PHPでint型をbytesに変換する方法を詳しく解説
Mar 06, 2024 pm 06:18 PM
PHPでint型をbytesに変換する方法を詳しく解説
Mar 06, 2024 pm 06:18 PM
PHPでint型をbyte型に変換する方法を詳しく解説 PHPでは、ネットワークデータ送信やファイル処理、暗号化アルゴリズムなどを扱う場合など、整数型(int)をバイト型(Byte)に変換する必要が生じることがよくあります。 。この記事では、int型をbyte型に変換する方法と具体的なコード例を詳しく紹介します。 1. int 型と byte の関係 コンピュータ分野では、基本データ型 int は整数を表しますが、byte (バイト) はコンピュータの記憶単位で、通常は 8 ビットのバイナリデータです
 Javaのreturn文とfinally文の実行順序は何ですか?
Apr 25, 2023 pm 07:55 PM
Javaのreturn文とfinally文の実行順序は何ですか?
Apr 25, 2023 pm 07:55 PM
ソースコード: publicclassReturnFinallyDemo{publicstaticvoidmain(String[]args){System.out.println(case1());}publicstaticintcase1(){intx;try{x=1;returnx;}finally{x=3;}}}#出力 上記のコードの出力は、単純に次のように結論付けることができます:finally の前に return が実行されます。バイトコード レベルで何が起こるかを見てみましょう。以下は、case1 メソッドのバイトコードの一部をインターセプトし、ソース コードを比較して、各命令の意味に注釈を付けます。
 修正: Windows 11 で Snipping ツールが機能しない
Aug 24, 2023 am 09:48 AM
修正: Windows 11 で Snipping ツールが機能しない
Aug 24, 2023 am 09:48 AM
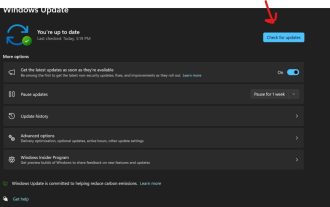
Windows 11 で Snipping Tool が機能しない理由 問題の根本原因を理解すると、適切な解決策を見つけるのに役立ちます。 Snipping Tool が正しく動作しない主な理由は次のとおりです。 フォーカス アシスタントがオンになっている: これにより、Snipping Tool が開かなくなります。破損したアプリケーション: 起動時にスニッピング ツールがクラッシュする場合は、破損している可能性があります。古いグラフィック ドライバー: 互換性のないドライバーは、スニッピング ツールに干渉する可能性があります。他のアプリケーションからの干渉: 実行中の他のアプリケーションが Snipping Tool と競合する可能性があります。証明書の有効期限が切れています: アップグレード プロセス中のエラーにより、この問題が発生する可能性があります。これらの簡単な解決策は、ほとんどのユーザーに適しており、特別な技術知識は必要ありません。 1. Windows および Microsoft Store アプリを更新する
 double型変数をint型に変換するC++プログラム
Aug 25, 2023 pm 08:25 PM
double型変数をint型に変換するC++プログラム
Aug 25, 2023 pm 08:25 PM
C++ では、int 型の変数は正または負の整数値のみを保持でき、10 進数値を保持できません。この目的に使用できる float 値と double 値があります。 double データ型は、小数点以下 7 桁までの小数を格納するために作成されました。整数から double データ型への変換は、コンパイラによって自動的に実行することも (「暗黙的」変換と呼ばれます)、プログラマがコンパイラに明示的に要求することもできます (「明示的」変換と呼ばれます)。次のセクションでは、さまざまな変換方法について説明します。暗黙的な変換 コンパイラは暗黙的な型変換を自動的に実行します。これを実現するには、浮動小数点型と整数型の 2 つの変数が必要です。浮動小数点値または変数を整数変数に代入するだけでは、コンパイラが他のすべてのことを処理します。
 int32の値の範囲はどれくらいですか?
Aug 11, 2023 pm 02:53 PM
int32の値の範囲はどれくらいですか?
Aug 11, 2023 pm 02:53 PM
int32 の値の範囲は、-2 の 31 乗から 2 の 31 乗 - 1、つまり -2147483648 ~ 2147483647 です。 int32 は符号付き整数型です。つまり、正の数、負の数、ゼロを表現できます。1 ビットを符号ビットの表現に使用し、残りの 31 ビットは数値の表現に使用されます。符号ビットを表すために 1 ビットが使用されるため、int32 の有効ビット数は 31 です。
 Go言語でintを文字列型に変換する方法
Jun 04, 2021 pm 03:56 PM
Go言語でintを文字列型に変換する方法
Jun 04, 2021 pm 03:56 PM
変換方法: 1. Itoa() 関数を使用し、構文 "strconv.Itoa(num)" 2. FormatInt() 関数を使用して、int 型データを指定した基数に変換し、文字列の形式で返します。構文「strconv .FormatInt(num,10)」。




