jsの基本アルゴリズム:バブルソート、二分探索
知識の拡張:
時間計算量: アルゴリズムの時間計算量は、アルゴリズムの実行時間を記述する関数です。時間の複雑さが低いほど、効率は高くなります。
自己理解: アルゴリズムの時間計算量は、それを n 回実行すると、時間計算量は O(n) になります。
1. バブルソート
分析: 1. 2 つの隣接する要素を比較し、前者の要素が後者の要素より大きい場合、位置を交換します。
2. 最初のラウンドでは、最後の要素が最大の要素でなければなりません。
3. 手順1に従って、隣接する2つの要素を比較します。この時点では、最後の要素がすでに最大であるため、最後の要素を比較する必要はありません。
function sort(elements){
for(var i=0;i<elements.length-1;i++){
for(var j=0;j<elements.length-i-1;j++){
if(elements[j]>elements[j+1]){
var swap=elements[j];
elements[j]=elements[j+1];
elements[j+1]=swap;
}
}
}
}
var elements = [3, 1, 5, 7, 2, 4, 9, 6, 10, 8];
console.log('before: ' + elements);
sort(elements);
console.log(' after: ' + elements);2. クイックソート
分析: クイックソートは、最初のソートパスでデータが 2 つの部分に分割され、一方の部分はもう一方の部分のすべてのデータよりも小さくなります。次に、それを再帰的に呼び出し、両側でクイックソートを実行します。
function quickSort(elements) {
if (elements.length <= 1) { return elements; }
var pivotIndex = Math.floor(elements.length / 2);
var pivot = elements.splice(pivotIndex, 1)[0];
var left = [];
var right = [];
for (var i = 0; i < elements.length; i++){
if (elements[i] < pivot) {
left.push(elements[i]);
} else {
right.push(elements[i]);
}
}
return quickSort(left).concat([pivot], quickSort(right));
};
var elements=[5,6,2,1,3,8,7,1.2,5.5,4.5];
alert(quickSort(elements));3. 挿入ソート
分析:
(1) 最初の要素から始めて、その要素はソートされたとみなすことができます
(2) 次の要素を取り出し、ソートされた要素シーケンスを後方から進めますフロントスキャン
(3) (並べ替えられた) 要素が新しい要素より大きい場合、要素を次の位置に移動します
(4) 並べ替えられた要素が以下になる位置が見つかるまで手順 3 を繰り返します。新しい要素
(5) 次の位置に新しい要素を挿入します
(6) 手順 2 を繰り返します
insertSort: function(elements) {
var i = 1,
j, step, key, len = elements.length;
for (; i < len; i++) {
step = j = i;
key = elements[j];
while (--j > -1) {
if (elements[j] > key) {
elements[j + 1] = elements[j];
} else {
break;
}
}
elements[j + 1] = key;
}
return elements;
}2. 二分探索
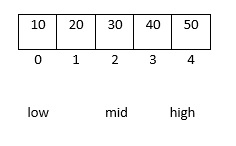
分析: 二分探索、二分探索とも言えます。まず、中間の値を見つけます。その値と比較して、大きい方を左に配置します。次に、両側の中央の値を見つけ、位置が見つかるまで上記の操作を続けます。
(1)再帰的メソッド
function binarySearch(data,item,start,end){
var end=end || data.length-1;
var start=start || 0;
var m=Math.floor((start+end)/2);
if(item==data[m]){
return m;
}else if(item<data[m]){
return binarySearch(data,item,start,m-1) //递归调用
}else{
return binarySearch(data,item,m+1,end);
}
return false;
}
var arr=[34,12,5,123,2,745,32,4];
binary(arr,5);(2)非再帰的メソッド
function binarySearch(data, item){
var h = data.length - 1,
l = 0;
while(l <= h){
var m = Math.floor((h + l) / 2);
if(data[m] == item){
return m;
}
if(item > data[m]){
l = m + 1;
}else{
h = m - 1;
}
}
return false;
}
var arr=[34,12,5,123,2,745,32,4];
binarySearch(arr,5);
ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 1658
1658
 14
14
 1415
1415
 52
52
 1309
1309
 25
25
 1257
1257
 29
29
 1231
1231
 24
24
 C# を使用して二分探索アルゴリズムを作成する方法
Sep 19, 2023 pm 12:42 PM
C# を使用して二分探索アルゴリズムを作成する方法
Sep 19, 2023 pm 12:42 PM
C# を使用してバイナリ検索アルゴリズムを作成する方法。バイナリ検索アルゴリズムは効率的な検索アルゴリズムです。時間計算量 O(logN) で順序付けられた配列内の特定の要素の位置を見つけます。 C# では、次の手順で二分探索アルゴリズムを作成できます。ステップ 1: データを準備する まず、検索対象のデータとしてソートされた配列を準備する必要があります。配列内の特定の要素の位置を見つけたいとします。 int[]data={1,3,5,7,9,11,13
 二分探索アルゴリズムを使用して数値の立方根を見つける Java プログラム
Aug 28, 2023 pm 01:33 PM
二分探索アルゴリズムを使用して数値の立方根を見つける Java プログラム
Aug 28, 2023 pm 01:33 PM
立方根は整数値であり、それ自体を 3 回続けて乗算すると元の値になります。この記事では、二分探索を使用して数値の立方根を見つける Java プログラムを作成します。数値の立方根を求めることは、二分探索アルゴリズムの応用です。この記事では、二分探索を使用して立方根を計算する方法について詳しく説明します。入出力例 例-1:入力:64出力:4 たとえば、64 の立方根は 4 で、出力は 4 になります。例-2:入力:216出力:6 たとえば、216 の立方根は 6 で、出力は 6 になります。二分検索 二分検索は、要素 (つまり、ソートされた配列内のキー) を見つけるために使用されるアルゴリズムです。バイナリアルゴリズムの動作
 マルチスレッド処理にpthreadを使用したC言語で書かれた二分探索プログラム
Aug 26, 2023 pm 12:45 PM
マルチスレッド処理にpthreadを使用したC言語で書かれた二分探索プログラム
Aug 26, 2023 pm 12:45 PM
二分探索法が最も適切かつ効果的な並べ替えアルゴリズムであることはわかっています。このアルゴリズムは、ソートされたシーケンスに対して機能します。アルゴリズムは単純で、要素を中央から見つけてリストを 2 つの部分に分割し、左のサブリストまたは右のサブリストに移動するだけです。私たちはそのアルゴリズムを知っています。次に、マルチスレッド環境でバイナリ検索手法を使用する方法を見ていきます。スレッドの数は、システムに存在するコアの数によって異なります。アイデアを理解するためにコードを見てみましょう。例#include<iostream>#defineMAX16#defineMAX_THREAD4usingnamespacestd;//placearr,keyandothervariabl
 C言語の二分探索アルゴリズムを使用して配列内の最小要素を見つけるにはどうすればよいですか?
Aug 25, 2023 pm 08:37 PM
C言語の二分探索アルゴリズムを使用して配列内の最小要素を見つけるにはどうすればよいですか?
Aug 25, 2023 pm 08:37 PM
C プログラミング言語には 2 つの検索手法が用意されています。それらは次のとおりです。 線形検索 二分検索 二分検索 この方法は、順序付きリストにのみ適しています。指定されたリストは 2 つの等しい部分に分割されます。指定されたキーがリストの中央の要素と比較されます。ここでは、次の 3 つのことが起こります: 中央の要素がキーワードに一致する場合、検索はここで正常に終了します。中央の要素がキーワードより大きい場合、検索は左側のパーティションで行われます。中央の要素がキーワードより小さい場合、検索は右側のパーティションで実行されます。入力(i/p) - 要素、キーワードの未ソートのリスト。出力 (o/p) - 成功 - キーワードが見つからない場合 - それ以外の場合 key=20mid=(low+high)/2 プログラム 1 以下は、二分探索の使用法です。
 Python を使用して二分探索アルゴリズムを実装するにはどうすればよいですか?
Sep 20, 2023 pm 01:24 PM
Python を使用して二分探索アルゴリズムを実装するにはどうすればよいですか?
Sep 20, 2023 pm 01:24 PM
Python を使用して二分探索アルゴリズムを実装するにはどうすればよいですか?二分探索アルゴリズムとも呼ばれる二分探索アルゴリズムは、効率的な検索アルゴリズムです。順序付けされた配列またはリストに対して機能し、ターゲット値を配列の中央の要素と比較することで検索を絞り込みます。以下では、Python で二分探索アルゴリズムを実装する方法と具体的なコード例を紹介します。アルゴリズムのアイデア: ターゲット値と配列の中央の要素を比較し、等しい場合は要素の位置を返します。ターゲット値が中央の要素より大きい場合は、右側の要素を返します。
 Javaを使用して二分探索アルゴリズムを実装する方法
Sep 19, 2023 pm 12:57 PM
Javaを使用して二分探索アルゴリズムを実装する方法
Sep 19, 2023 pm 12:57 PM
Java を使用して二分探索アルゴリズムを実装する方法 二分探索アルゴリズムは、ソートされた配列に適した効率的な検索方法です。基本的な考え方は、検索範囲を継続的に絞り込み、検索値と配列の中央の要素を比較し、比較結果に基づいて目的の要素が見つかるまで左半分を検索し続けるか右半分を検索し続けるかを決定することです。検索範囲が空になります。以下では、Java で二分探索アルゴリズムを実装する方法を詳しく紹介します。ステップ 1: バイナリ検索メソッド publicclassBinarySearch を実装する
 PHP アルゴリズム分析: 二分探索アルゴリズムを使用して、順序付けされた配列内の要素をすばやく見つけるにはどうすればよいですか?
Sep 19, 2023 pm 01:14 PM
PHP アルゴリズム分析: 二分探索アルゴリズムを使用して、順序付けされた配列内の要素をすばやく見つけるにはどうすればよいですか?
Sep 19, 2023 pm 01:14 PM
PHP アルゴリズム分析: 二分探索アルゴリズムを使用して、順序付けされた配列内の要素をすばやく見つけるにはどうすればよいですか?概要: 二分探索アルゴリズムは、順序付けされた配列内の特定の要素を見つけるのに適した効率的な検索アルゴリズムです。この記事では、二分探索アルゴリズムの原理を詳しく紹介し、PHP コード例を示します。原理: 二分探索アルゴリズムは、探索範囲を半分に減らすことを繰り返すことで、ターゲット要素を迅速に見つけます。処理としては、まず検索範囲を配列の先頭と末尾に絞り、次に中央要素のインデックスを計算して対象要素と比較し、その後、検索範囲を配列の先頭と末尾に絞ります。
 C プログラムでは、浮動小数点演算を使用せずに二分探索アルゴリズムを使用して有理数を検索します。
Aug 27, 2023 pm 06:05 PM
C プログラムでは、浮動小数点演算を使用せずに二分探索アルゴリズムを使用して有理数を検索します。
Aug 27, 2023 pm 06:05 PM
この問題では、ソートされた有理数の配列が与えられます。浮動小数点演算を使用せずに、この有理数の配列の特定の要素を検索するには、二分探索アルゴリズムを使用する必要があります。有理数は、p/q の形式で表される数値です。ここで、p と q は両方とも整数です。たとえば、2/3、1/5。二分探索は、配列の中央を検索して要素を見つける検索手法です。浮動小数点演算が許可されていない二分探索を使用して、ソートされた有理数の配列内の要素を検索するために使用されます。分子と分母を比較して、どちらの要素が大きいか、またはどちらの要素が大きいかを調べます。例 #include<stdio.h>structRational{ &am というプログラムを作成してみましょう。




