キャンバス差分機能の素晴らしい使い方

この記事では、この効果がどのように達成されるかを分析します。ソースコードについて混乱している場合は、分析を読むと突然理解できると思います。まず、レンダリング:

1. 原理分析

前の記事の単純な水の波のアニメーション効果と比較して、この記事のアニメーション効果はマウスと対話できるだけでなく、波の形成も行うことができます。より自然で、より一貫した物理法則です。全体の形成過程はアニメーションの通りで、液面の位置でマウスをクリックすると、ここの液面が比較的大きく変動し、その振動が両側に広がります。エネルギーが減衰すると、その後の振動の振幅はどんどん低くなり、最終的にエネルギーはゼロに減衰し、ページは穏やかになります。とても神秘的だと思いませんか？毛主席は物体の表面現象に騙されないようにと言いました（誰が言ったか分かりませんo(^▽^)o）。以下では、原則を段階的に分析していきます。

まず、静的な状態では、液体表面全体が長方形に等しいことがわかります。液体表面の位置をクリックすると、それに応じて長方形が変化します。しかし実際には、長方形全体が変化したのではなく、長方形の上端のみが変化しました。では、長方形の上端だけを変更するにはどうすればよいでしょうか?その秘密は、長方形の上端が単に左点から右点までの lineTo() ではないことです。代わりに、多くの点 lineTo() で構成されます。このように理解するのは簡単ではないかもしれませんが、画像を見て話しましょう:

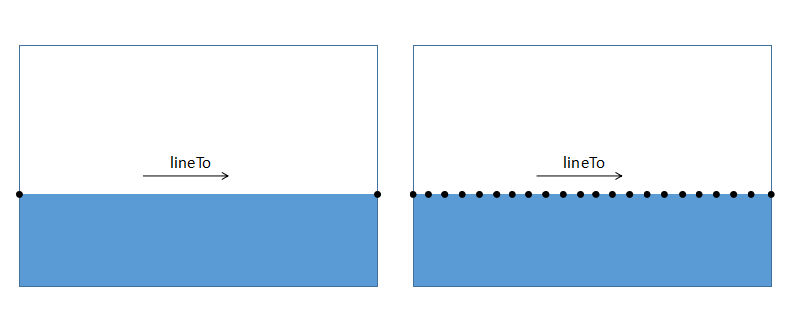
上部に多くの点を設定します。これらの点の座標は同じですが、特定の距離で区切られています。水平方向の距離。このように、静止した状態では普通の長方形と変わらないことがわかります。これらの点の位置を変更すると、同時に長方形の形状も変更され、さまざまな効果を生み出すことができます。

2. 微分方程式

微分方程式に関しては頭が痛くなる人も多いかもしれませんが、方法はありません。この知識ポイントは高度な数学の微分方程式に関するセクションにあります。理解できない場合は忘れてください。以下のような使い方も覚えておくと良いですが、オシャレのために簡単に紹介します。

数学における漸化式は、差分方程式とも呼ばれ、シーケンスを再帰的に定義する方程式です。シーケンス内の各項目は、前の項目の関数として定義されます。単純に定義された漸化関係の中には、非常に複雑な (カオス的な) 特性を示すものもあります。それらは数学の非線形解析の分野に属します。

シーケンス内の各項目は前の項目の関数として定義されることを覚えておいてください。これが私たちが使用する原則です。彼の画像を matalab で描画すると、次のようになります:

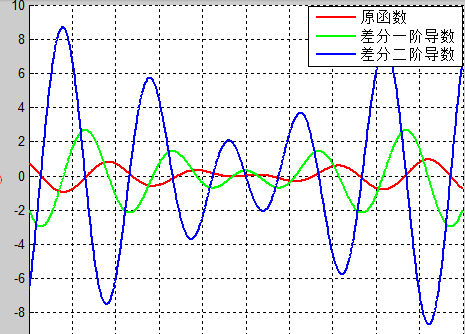
元の関数に注目してください。赤い曲線で十分です。水の波のように見えますか?やるべきことは、このような波形に従って点の束を配置することです。

3. コードの実装

1. 準備

さあ、みんなが大好きなコーディングの時間です。まず、ポイント クラス Vertexes を作成します。その機能は、次のように vertex.js にあります:

function Vertex(x,y,baseY){
        this.baseY = baseY;         //基线
        this.x = x;                 //点的坐标
        this.y = y;            
        this.vy = 0;                //竖直方向的速度
        this.targetY = 0;           //目标位置
        this.friction = 0.15;       //摩擦力
        this.deceleration = 0.95;   //减速
    }
//y坐标更新
Vertex.prototype.updateY = function(diffVal){
        this.targetY = diffVal + this.baseY;   //改变目标位置
        this.vy += (this.targetY - this.y);       //速度
        this.vy *= this.deceleration;
        this.y += this.vy * this.friction;     //改变坐标竖直方向的位置
    }

この関数を使用して、ポイントの束を作成します。メインファイルのindex.jsに戻ります。最初に使用する必要があるものをいくつか初期化しましょう:

var canvas = document.getElementById('canvas'),
    ctx = canvas.getContext('2d'),
    W = window.innerWidth;
    H = window.innerHeight;

    canvas.width = W;
    canvas.height = H;

var color1 = "#6ca0f6",    //矩形1的颜色
    color2 = "#367aec";   //矩形2的颜色
    
var vertexes = [],    //顶点坐标
    verNum = 250,     //顶点数
    diffPt = [],      //差分值

然后，创建点并把它push进vertexes中，同时也创建相应数量的差分值，同样把它放到diffPt数组中，这样每个点都有了对应的差分值。

for(var i=0; i<verNum; i++){
    vertexes[i] = new Vertex(W/(verNum-1)*i, H/2, H/2);
    diffPt[i] = 0;                                         //初始值都为0
}

结果是，每个顶点的y坐标都在（H/2）的高度，水平坐标每隔一定的间隔取一个点。在这里是每隔4.5个像素取一个点，这与你canvas的宽度和点的数目有关。这样我们就把点创建完成了，来绘制一下看看效果。

代码如下：

function draw(){
        
        //矩形1
        ctx.save()
        ctx.fillStyle = color1;
        ctx.beginPath();
        ctx.moveTo(0, H);
        ctx.lineTo(vertexes[0].x, vertexes[0].y);
        for(var i=1; i<vertexes.length; i++){
            ctx.lineTo(vertexes[i].x, vertexes[i].y);
        }
        ctx.lineTo(W,H);
        ctx.lineTo(0,H);
        ctx.fill();
        ctx.restore();
        
        //矩形2
        ctx.save();
        ctx.fillStyle = color2;
        ctx.beginPath();
        ctx.moveTo(0, H);
        ctx.lineTo(vertexes[0].x, vertexes[0].y+5);
        for(var i=1; i<vertexes.length; i++){
            ctx.lineTo(vertexes[i].x, vertexes[i].y+5);
        }
        ctx.lineTo(W, H);
        ctx.lineTo(0, H);
        ctx.fill();
        ctx.restore();
}

就像你看到的那样此时我们的液面完全是静止的（因为没更新点嘛）。之所以要绘制两个矩形，你看看效果图就明白了，只是为了更好看，你完全可以绘制第三层，第四层。下面我们就来更新这些点的坐标。

2.核心代码

点的更新我们放在了update函数中。首先，我们设置一个初始的震荡点,缓冲变量和初始差分值。

var vPos = 125;  //震荡点
var dd = 15;     //缓冲
var autoDiff = 1000;  //初始差分值

这里的震荡点就是我们的起震位置，意思是vertexes中的第125号点开始起震，它对应的差分值就是autoDiff。它的改变会引起其他点的变化，从而达到更新其他差分值的效果。

function update(){
        autoDiff -= autoDiff*0.9;        //1
        diffPt[vPos] = autoDiff;         

        //左侧
        for(var i=vPos-1; i>0; i--){     //2
            var d = vPos-i;
            if(d > dd){
                d=dd;
            }
            diffPt[i]-=(diffPt[i] - diffPt[i+1])*(1-0.01*d);
        }
        //右侧
        for(var i=vPos+1; i<verNum; i++){   //3
            var d = i-vPos;
            if(d>dd){
                d=dd;
            }
            diffPt[i] -= (diffPt[i] - diffPt[i-1])*(1-0.01*d);
        }

        //更新Y坐标
        for(var i=0; i<vertexes.length; i++){  //4
            vertexes[i].updateY(diffPt[i]);
        }
    }

现在我们对上面的部分做详细解释：
代码1： 我们设置了起震位置的差分偏移量为autoDiff=100,注意autoDiff -= autoDiff*0.9;, 也就是说它的值每一帧都会变化。

代码2：为起震位置的左边，主要关注diffPt[i]-=(diffPt[i] - diffPt[i+1])*(1-0.01*d);这一行。i的起始位置为124，默认差分值为0。稍作简单推算，你会发现，经过更新后第124号点的差分值为99，同理第123号为97.02。以此类推，我们就可以得到第一帧的所有点的差分值。右边同理。

代码4：在得到第一帧的差分值后就该调用每个点的更新函数了，并且传入计算好的差分值。形成的效果如下图所示

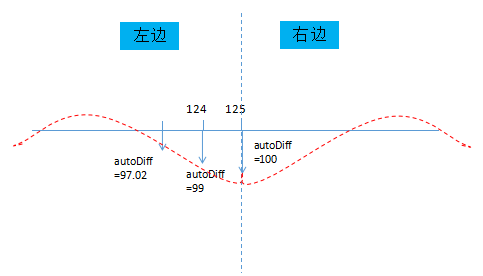
看一下updateY函数，我们把目标位置targetY设置为差分值diffVal和基线baseY的和。然后，通过距离计算需要运动的速度vy,最后将速度作用于点的纵坐标。这一段是不是与弹性动画缓动动画那一节很相似呢？

在缓冲系数dd的作用下，两侧的波会在扩散的过程中越来越小，最后趋近于0.我们也是通过这个变量去控制液体的粘度系数，达到粘稠度高的物体扩散的越缓慢并且起伏比较低，粘稠度低的物体扩散迅速但起伏大的效果。

随后，因为autoDiff的不断衰减，不同幅值波形的叠加形成波浪效果，最终衰减到0.液面也就趋于平静了。

现在，我们把update()和draw()放入动画循环中你就会看到水波起伏然后趋于平静的效果。

(function drawframe(){
        ctx.clearRect(0, 0, W, H);
        window.requestAnimationFrame(drawframe, canvas);
        update()
        draw();
    })()

3.鼠标交互

上面的代码已经实现了波浪动画的效果，但是震荡完成后就平静了，不会再发生震荡的效果。这一步我们就来实现点哪，哪震的效果。实现的思路很简单：水波之所以区域平静是因为起震位置的差分值不断衰减的结果，我们只需要在点击鼠标的位置重设autoDiff就可以了。此外，起震点的位置也要变成鼠标点击的位置。代码如下：

canvas.addEventListener('mousedown', function(e){
        var mouse = {x:null, y:null};

        if(e.pageX||e.pageY){
            mouse.x = e.pageX;
            mouse.y = e.pageY;
        }else{
            mouse.x = e.clientX + document.body.scrollLeft +document.documentElement.scrollLeft;
            mouse.y = e.clientY + document.body.scrollTop +document.documentElement.scrollTop;
        }

        //重设差分值
        if(mouse.y>(H/2-50) && mouse.y<(H/2 +50)){
            autoDiff = 1000;
            vPos = 1 + Math.floor((verNum - 2) * mouse.x / W);
            diffPt[vPos] = autoDiff;
        }

        console.log(mouse.x, mouse.y)

    }, false)

在获取鼠标位置这里应该注意一点，我们没有减去canvas的偏移量，这是因为在这里canvas做的是全屏设置。所以，如果你的画布并不是全屏大小，建议你使用我们的utils.js文件中的方法captureMouse来获取鼠标的坐标。

另外在判断鼠标是否点击在了液面上，我们设定了一个比较宽的范围，上下共100px。这样做的目的是让用户很容易就能触发这个事件，而不是只在页面那唯一的一个值上才能触发。这种做法相信你以前做过，对于比较小的物体我们会遮罩一个大一些的透明物体，然后在该物体上做事件的触发，便于用户操作。