フィボナッチ数列の一般用語を実現する 7 つの方法

1: 再帰的実装
式 f[n]=f[n-1]+f[n-2] を使用し、順番に再帰的に計算します。再帰終了条件は f[1]=1, f[2] です。 =1。
2: 配列の実装
空間計算量と時間計算量は両方とも 0(n) で、効率は平均的で、再帰よりも高速です。
3: Vector の実装
時間計算量は 0(n) ですが、ベクトルが効率的かどうかはわかりません。リソースを占有します。
4: Queue の実装
もちろん、時間計算量と空間計算量は配列よりも Queue の方が適していますが、これには queue が最適です
f(n) =f (n-1)+f(n-2)、f(n) がキューに追加された後、f(n) は f(n-1) と f(n-2) にのみ関連します。 n-2) デキューできます。
5: 反復実装
反復実装は、時間計算量が 0(n)、空間計算量が 0(1) で最も効率的です。
六：数式の実装
Baiduを検索していたら、フィボナッチ数列には数式があり、その数式を使用して計算できることを発見しました。
double型の精度が十分ではないため、プログラムで計算した結果には誤差が生じますが、式を展開して計算すると正しい結果になります。
完全な実装コードは次のとおりです:

#include "iostream"
#include "queue"
#include "cmath"
using namespace std;
int fib1(int index)     //递归实现
{
 if(index<1)
 {
  return -1;
 }
 if(index==1 || index==2)
  return 1;
 return fib1(index-1)+fib1(index-2);
}
int fib2(int index)     //数组实现
{
 if(index<1)
 {
  return -1;
 }
 if(index<3)
 {
  return 1;
 }
 int *a=new int[index];
 a[0]=a[1]=1;
 for(int i=2;i<index;i++)
  a[i]=a[i-1]+a[i-2];
 int m=a[index-1];
 delete a;         //释放内存空间
 return m;
}
int fib3(int index)           //借用vector<int>实现
{
 if(index<1)
 {
  return -1;
 }
 vector<int> a(2,1);      //创建一个含有2个元素都为1的向量
 a.reserve(3);
 for(int i=2;i<index;i++)
 {
  a.insert(a.begin(),a.at(0)+a.at(1));
  a.pop_back();
 }
 return a.at(0);
} 
int fib4(int index)       //队列实现
{
 if(index<1)
 {
  return -1;
 }
 queue<int>q;
 q.push(1);
 q.push(1);
 for(int i=2;i<index;i++)
 {
  q.push(q.front()+q.back());
  q.pop();
 }
 return q.back();
}
int fib5(int n)          //迭代实现
{
 int i,a=1,b=1,c=1;
 if(n<1)
 {
  return -1;
 }
 for(i=2;i<n;i++)
 {
  c=a+b;     //辗转相加法（类似于求最大公约数的辗转相除法）
  a=b;
  b=c;
 }
 return c;
}
int fib6(int n)
{
 double gh5=sqrt((double)5);
 return (pow((1+gh5),n)-pow((1-gh5),n))/(pow((double)2,n)*gh5);
} 
int main(void)
{
 printf("%d\n",fib3(6));
 system("pause");
 return 0;
}

7: 二部行列法

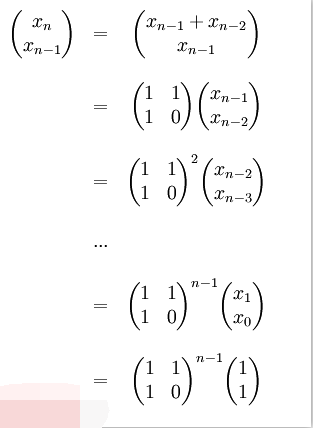
上記のように、フィボナッチ数列の任意の項目は行列累乗を使用して計算でき、n 乗はログ時間で計算できます。
コードは以下に掲載されています:

void multiply(int c[2][2],int a[2][2],int b[2][2],int mod)
{
 int tmp[4];
 tmp[0]=a[0][0]*b[0][0]+a[0][1]*b[1][0];
 tmp[1]=a[0][0]*b[0][1]+a[0][1]*b[1][1];
 tmp[2]=a[1][0]*b[0][0]+a[1][1]*b[1][0];
 tmp[3]=a[1][0]*b[0][1]+a[1][1]*b[1][1];
 c[0][0]=tmp[0]%mod;
 c[0][1]=tmp[1]%mod;
 c[1][0]=tmp[2]%mod;
 c[1][1]=tmp[3]%mod;
}//计算矩阵乘法，c=a*b
int fibonacci(int n,int mod)//mod表示数字太大时需要模的数
{
 if(n==0)return 0;
 else if(n<=2)return 1;//这里表示第0项为0，第1，2项为1
 int a[2][2]={{1,1},{1,0}};
 int result[2][2]={{1,0},{0,1}};//初始化为单位矩阵
 int s;
 n-=2;
 while(n>0)
 {
  if(n%2 == 1)
   multiply(result,result,a,mod);
  multiply(a,a,a,mod);
  n /= 2;
 }//二分法求矩阵幂
 s=(result[0][0]+result[0][1])%mod;//结果
 return s;
}

aのn乗関数を計算するための二分法を添付します。

int pow(int a,int n)
{
 int ans=1;
 while(n)
 {
  if(n&1)
   ans*=a;
  a*=a;
  n>>=1;
 }
 return ans;
}

フィボナッチ数列の一般項を求める 7 つの実装方法に関するその他の関連記事については、PHP 中国語 Web サイトに注目してください。