Mysql-index データ構造

1. はじめに:

私たちの生活の中で、駅で見る電車の時刻表や辞書ディレクトリなど、インデックス効果を確認できるアプリケーションをエクスポートします。それらの機能はインデックスの機能であり、取得するデータの範囲を継続的に絞り込むことで最終的に望ましい結果をフィルタリングし、同時にランダムなイベントを連続したイベントに変換します。つまり、常に同じ検索方法を使用して、データをロックします (辞書の A-Z 検索)。

人生の例 - 電車に乗る: 電車に乗って故郷に帰ります。電車に乗りたいときに電車の時刻表がなかったら、最悪の結果は、すべての電車の停留所に行かなければならないことです。乗りたい電車があるのに、時刻表があると行きたい電車がどこに止まるのかがすぐに分かり、行きたい電車をいちいち確認する必要がなく、すぐにそこに行くことができるのでスピードアップします。訪問。この列車時刻表はデータベースのインデックスです。

2. ディスク原理:

この部分は文章理論が多く、読むだけで頭が痛くなります。興味があれば読んでください。この部分の結論を 1 つ覚えておいてください:

可能な限りデータを読み取る [オペレーティング システムとの I/O 対話の数を減らす]。

興味がない場合は、スキップして次のパートに進んでください。

データベースの実装は比較的複雑であり、パフォーマンスを向上させるために、毎回データの一部をメモリに読み込むことができます。メモリへのアクセスの 100,000 倍であるため、検索ツリーは複雑なアプリケーション シナリオに対応することが困難です。ディスクへのアクセスについては前述したので、ここではディスク IO と事前読み取りについて簡単に説明します。データの読み取りにかかる時間は、シーク時間、回転遅延の 3 つのカテゴリに分類されます。 、および送信時間、
a) · シーク時間: 磁気アームが指定されたトラックに移動するのに必要な時間、主流のディスクは通常 5 ミリ秒未満です。 b) 回転遅延: よく聞くディスク速度です。 7200 rpm のディスクなど、1 分間に 7200 回回転できることを意味します。つまり、回転遅延は 1/120/2 = 4.17 ミリ秒になります。ディスクからのデータの読み取りまたはディスクへのデータの書き込みにかかる時間は、通常は 10 分の 1 ミリ秒以内で、最初の 2 回に比べて無視できます。
(非常に詳細な記事を読みました: http://wdxtub.com/2016/04/16/thin-csapp-3/)

すると、ディスクにアクセスする時間、つまりディスク IO の時間は5 + 4.17 = 約 9 ミリ秒に相当します。これはかなり良いように思えますが、命令は自然などの電気に依存するため、500 MIPS (1 秒あたりの命令数) のマシンは 1 秒あたり 5 億命令を実行できることを知っておく必要があります。つまり、1 つの IO を実行するには 400,000 の命令が必要であり、そのたびに 9 ミリ秒かかるのは明らかに大惨事です。

結論としては、オペレーティング システムの I/O インタラクションの数を減らします。

(毎回 IO によって読み取られるデータをページと呼びます。ページ上のデータの具体的なサイズはオペレーティング システムによって異なりますが、通常は 4k または 8k です。つまり、ページ内のデータを読み取るとき、実際のデータは 1 つだけです前回は IO が発生しました)

3. インデックスとは:

データベース システムを使用する過程で、データ クエリは最も頻繁に使用されるデータ操作です。

最も基本的なクエリ アルゴリズムは、もちろん、テーブルを走査し、行の値が検索するキーワードと等しいかどうかを行ごとに照合します。その時間計算量は O(n) です。ただし、時間計算量が O(n) のアルゴリズムは、小さなテーブルや負荷の軽いデータベースでも良好なパフォーマンスを達成できます。しかし、データが増加すると、時間計算量が O(n) のアルゴリズムは明らかに悪く、パフォーマンスは急速に低下します。

幸いなことに、コンピューターサイエンスの発展により、二分探索や二分探索など、より優れた検索アルゴリズムが数多く提供されました。 木探索）など少し分析すると、各検索アルゴリズムは特定のデータ構造にのみ適用できることがわかります。たとえば、二分探索では取得したデータを順序付けする必要がありますが、二分木検索では二分探索木にのみ適用できます。データ自体 組織構造はさまざまなデータ構造を完全に満たすことはできません (たとえば、両方の列を同時に順番に整理することは理論的に不可能です)。そのため、データベース システムはデータに加えて、特定の検索を満たすデータ構造も維持します。アルゴリズム。構造は何らかの方法でデータを参照 (ポイント) し、これらのデータ構造に高度な検索アルゴリズムを実装できます。このデータ構造がインデックスです。

4. MySQL の B-Tree インデックス (技術的には B+Tree)

さて、ここからがこの記事の核心です。

MySQL には、B ツリー インデックス、ハッシュ インデックス、フルテキスト インデックス、R ツリー インデックスという 4 つの主なタイプのインデックスがあります。主にB-Treeインデックスを分析します。 (B: バランスとはバイナリツリーではなくバランスを意味します)

1. b+ ツリーのデータ構造の詳細な説明

上の図は b+tree です (innodb エンジンの下では、myisam エンジンの下の B+ 構造とは異なります。端的に言えば、クラスター化インデックスと非クラスター化インデックスの違いです。詳細については、を参照してください) :

Mysql-cluster クラスター インデックス

水色のブロックはディスク ブロックと呼ばれ、各ディスク ブロックには複数のデータ項目 (濃い青で表示、範囲: [(M/2)-1, M-) が含まれていることがわかります。たとえば、ディスク ブロック 1 にはデータ項目 17 と 35 が含まれ、P1 は 17 未満のディスク ブロックを表し、P2 はデータ項目を表します。 17 ～ 35 のディスク。ブロック、P3 は 35 より大きいディスク ブロックを表します。実際のデータはリーフ ノード、つまり 3、5、9、10、13、15、28、29、36、60、75、79、90 に存在します。 , 99 のみ。実際のデータ (B+ の特徴) は保存されません。たとえば、17 と 35 は実際にはデータ テーブルに存在しません。 B+ ツリー

の検索プロセスは、図に示すように、データ項目 29 を検索する場合、まずディスク ブロック 1 をディスクからメモリにロードします。このとき、IO が発生します。メモリ内でバイナリ検索を実行し、29 が 17 ～ 35 の間にあることを確認し、ディスク ブロック 1 の P2 ポインタをロックします。ディスク ブロック 3 がロードされるのと比較して非常に短いため、メモリ時間は無視できます。ディスク ブロック 1 の P2 ポインタのディスク アドレスを介してディスクをメモリにロードします。2 番目の IO が発生し、29 は 26 と 30 の間にあり、ディスク ブロック 3 の P2 ポインタをロックし、ポインタを介してディスク ブロック 8 をメモリにロードします。同時に、3 番目の IO がメモリ内で実行され、29 が見つかり、クエリは終了します。実際には、b+ ツリーは数百万のデータを表す可能性があります。数百万回のデータ検索に必要な IO は 3 回だけですが、インデックスがない場合、各データ項目に 1 回の IO が必要になるため、合計 100 万回の IO が必要となり、明らかにコストが高くなります。 、非常に高いです

(質問???、前述したように、INNOBD の B+ ツリーはクラスター化インデックス タイプであり、実際のデータとインデックスのリーフ ノードがまとめられているため、問題は、私がどのくらい弱いかということです。それは可能ですか?各インデックスの下にデータが格納されているということですか? そうでない場合は、データ構造を使用してそれを表現する方法を教えてください。各テーブルにはクラスター化インデックスが 1 つだけあり、補助インデックスは複数ありません。データではなく、データが保存されているプラ​​イマリ インデックスを指すポインターです。

1) 上記の分析を通じて、IO の数は b+ の高さ h に依存することがわかります。現在のデータテーブルのデータを N とし、各ディスクブロックのデータ数を m とすると、データ量 N が一定の場合、m が大きくなるほど h=㏒(m +1)N となります。 、h と m が小さい方。 = ディスク ブロックのサイズ / データ項目のサイズ。ディスク ブロックのサイズはデータ ページのサイズであり、データ項目が占有するスペースが小さい場合、データ項目の数は次のようになります。より多くなり、ツリーの高さ h も低くなります。I/O も少なくなります。このため、各データ項目、つまりインデックス フィールドはできるだけ小さくする必要があります。

たとえば、負の例を挙げると、int は 4 バイトを占めますが、これは bigint の 8 バイトの半分です。これが、b+ ツリーが実際のデータを内部ノードではなくリーフ ノードに配置する必要がある理由です。内部ノードに配置されると、ディスク ブロックのデータ項目が大幅に減少し (上記のパート 2 の原理を参照)、ツリーが身長の増加。データ項目が 1 の場合、線形テーブルに縮退します。以下の通りです。

左の構造であれば I/O 回数は 3 回、右の線形テーブルであれば I/O 回数は 6 回であることがわかります。より多くの IO があること

結論:

1. インデックスとして設定するフィールド len は小さくする必要があります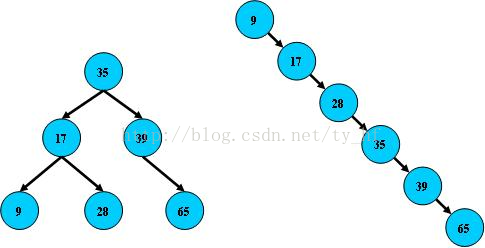

2. ジョイント インデックスを実行する場合、ジョイント フィールドの数も小さくする必要があります。

2) b+ ツリーのデータ項目が複合データ構造 (複数列インデックス) である場合、(名前、年齢、性別)、b+ 数値が検索の構築に使用されます。左から右の順にツリーを作成します。

たとえば、(Zhang San, 20, F) のようなデータが取得された場合、b+ ツリーは最初に名前を比較して次の検索方向を決定します。名前が同じ場合は、年齢と性別を順に比較します。そして最後に取得したデータを取得します。しかし、(20,F) のような名前のないデータが来ると、b+ ツリーは次にどのノードをチェックすればよいのかわかりません。これは、検索ツリーを確立するときに名前が最初の比較要素であり、それが必要であるためです。最初に名前に基づいて検索し、次にどこを探すかを確認します。

たとえば、(Zhang San, F) のようなデータを取得する場合、b+ ツリーは名前を使用して検索方向を指定できますが、次のフィールド age が欠落しているため、名前が Zhang と等しいすべてのデータしか検索できません。 San、次に性別の一致は F のデータです。これは非常に重要なプロパティ、つまりインデックスの左端の一致特徴です。

2 つの結論をマップします。

1. 左端の一致する特徴、結合インデックスは左から右に読み取られます

2. 複数列のインデックスがある場合、左からインデックスを作成する必要はありません。右へ (a,b,c) したがって、(a)、(a,b) を確立する必要はありません

3. さらなる結論: Mysql-index の概要 http://blog.csdn.net/ty_hf/article/details/53526405

上記は Mysql-index データ構造の内容です。さらに関連する内容については、PHP 中国語 Web サイト (www.php.cn) を参照してください。 ）！