
スタック
スタックはスタックとも呼ばれ、挿入と削除の操作はスタックの先頭で実行され、先入れ、後出し、後入れの規則に従って動作します。 -先出し。
下の写真のように
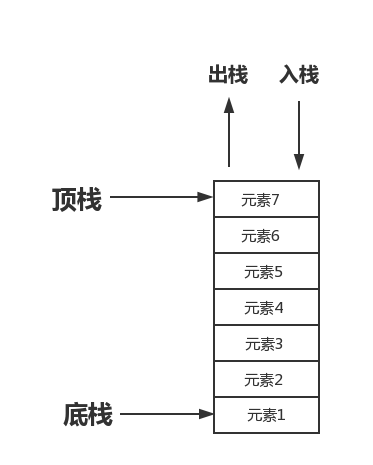
例えば、銃の弾倉では、発射時に弾倉に入れられた最初の弾が最後になり、弾倉に入れられた最後の弾が発射されます。そのとき、最初のものが発売されました。
スタックインターフェース
スタックを作成する場合、スタックを操作するために次のインターフェースが必要です
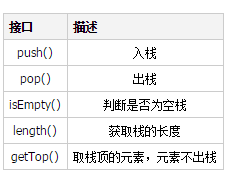
スタックが上記のインターフェースを必要とすることを知った後、Pythonではリストはスタックに似ています。提供されるインターフェイスは次のとおりです:
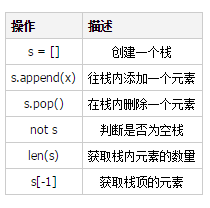
Python でのスタック インターフェイスの使用例:
# 创建一个栈 In [1]: s = [] # 往栈内添加一个元素 In [2]: s.append(1) In [3]: s Out[3]: [1] # 删除栈内的一个元素 In [4]: s.pop() Out[4]: 1 In [5]: s Out[5]: [] # 判断栈是否为空 In [6]: not s Out[6]: True In [7]: s.append(1) In [8]: not s Out[8]: False # 获取栈内元素的数量 In [9]: len(s) Out[9]: 1 In [10]: s.append(2) In [11]: s.append(3) # 取栈顶的元素 In [12]: s[-1] Out[12]: 3
多数の例
スタックの基本概念を理解した後、わかりやすくするためにさらにいくつかの例を見てみましょう。スタックの理解。
括弧の一致
質問
式に 3 つの角括弧 ()、[]、{} を含めることができる場合、ネスト順序は任意です。例:
正しい形式
{()[()]},[{({})}]不正な形式
[(]),[()),(()}
Write式文字列内の括弧の一致が正しいかどうかを判断する関数
アイデア
まだ見つかっていない左括弧を格納する空のスタックを作成します。
便利な文字列、左括弧に遭遇したときにスタックをプッシュします。右の括弧に到達したら、一致させるためにスタックから左の括弧をポップします。
2 番目のステップで、スタックが空のときに右の括弧が見つかった場合は、左の括弧が欠落しており、一致しないことを意味します。 2 番目のステップのトラバーサルの終わり、スタックは空ではありません。これは、右括弧が欠落していて一致しないことを示します
コードを解決します
よりよく理解するために、pycharm でポイントを分割することをお勧めします
#!/use/bin/env python
# _*_ coding:utf-8 _*_
LEFT = {'(', '[', '{'} # 左括号
RIGHT = {')', ']', '}'} # 右括号
def match(expr):
"""
:param expr: 传过来的字符串
:return: 返回是否是正确的
"""
stack = [] # 创建一个栈
for brackets in expr: # 迭代传过来的所有字符串
if brackets in LEFT: # 如果当前字符在左括号内
stack.append(brackets) # 把当前左括号入栈
elif brackets in RIGHT: # 如果是右括号
if not stack or not 1 <= ord(brackets) - ord(stack[-1]) <= 2:
# 如果当前栈为空,()]
# 如果右括号减去左括号的值不是小于等于2大于等于1
return False # 返回False
stack.pop() # 删除左括号
return not stack # 如果栈内没有值则返回True,否则返回False
result = match('[(){()}]')
print(result)
迷路問題
質問
2 次元配列は単純な迷路を表します。0 は通路を表し、1 はブロックを表します。各点で、マウスは南東、北西の 4 つの隣接する点に移動できます。マウスが迷路を歩くことをシミュレートし、道の入り口から出口までの経路を見つけるアルゴリズムを設計します。
写真の通り
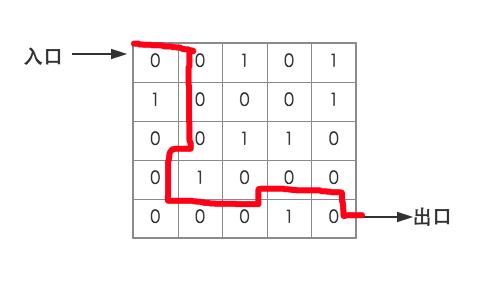 正しい出口は写真の赤い線で示されています
正しい出口は写真の赤い線で示されています
アイデア
スタックを使用して入り口から出口までのマウスの経路を記録します
歩いた後特定のポイントに到達したら、そのポイントを置きます。左側のスタックを押してポイント値を 1 に設定し、通過したことを示します
近くの 4 つのポイントから到達可能なポイントのいずれかを選択し、そのポイントまで歩きます
;特定のポイントに到達した後、そのポイントに近づいた場合 4 つのポイントを通過できなかった場合は、その時点でスタックから後退し、一歩下がって他のポイントを試します。出口が見つかるまで 2 番目、3 番目、および 4 番目のステップを実行します。括弧は必要ありません:
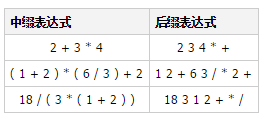
後置式の評価関数を実装するプログラムを作成します。 アイデア計算するオペランドを保存するスタックを作成します。
文字列をトラバースし、演算記号に遭遇したときにオペランドをスタックにプッシュし、演算記号に遭遇したときにスタックからオペランドをポップします(n回)。対応する計算を実行すると、計算結果は新しいオペランドとしてスタックにプッシュされ、計算を待機します
上記のプロセスに従い、式全体を走査し、最終結果のみがスタックに残ります。
コード#!/use/bin/env python # _*_ coding:utf-8 _*_ def initMaze(): """ :return: 初始化迷宫 """ maze = [[0] * 7 for _ in range(5 + 2)] # 用列表解析创建一个7*7的二维数组,为了确保迷宫四周都是墙 walls = [ # 记录了墙的位置 (1, 3), (2, 1), (2, 5), (3, 3), (3, 4), (4, 2), # (4, 3), # 如果把(4, 3)点也设置为墙,那么整个迷宫是走不出去的,所以会返回一个空列表 (5, 4) ] for i in range(7): # 把迷宫的四周设置成墙 maze[i][0] = maze[i][-1] = 1 maze[0][i] = maze[-1][i] = 1 for i, j in walls: # 把所有墙的点设置为1 maze[i][j] = 1 return maze """ [1, 1, 1, 1, 1, 1, 1] [1, 0, 0, 1, 0, 0, 1] [1, 1, 0, 0, 0, 1, 1] [1, 0, 0, 1, 1, 0, 1] [1, 0, 1, 0, 0, 0, 1] [1, 0, 0, 0, 1, 0, 1] [1, 1, 1, 1, 1, 1, 1] """ def path(maze, start, end): """ :param maze: 迷宫 :param start: 起始点 :param end: 结束点 :return: 行走的每个点 """ i, j = start # 分解起始点的坐标 ei, ej = end # 分解结束点的左边 stack = [(i, j)] # 创建一个栈,并让老鼠站到起始点的位置 maze[i][j] = 1 # 走过的路置为1 while stack: # 栈不为空的时候继续走,否则退出 i, j = stack[-1] # 获取当前老鼠所站的位置点 if (i, j) == (ei, ej): break # 如果老鼠找到了出口 for di, dj in [(0, -1), (0, 1), (-1, 0), (1, 0)]: # 左右上下 if maze[i + di][j + dj] == 0: # 如果当前点可走 maze[i + di][j + dj] = 1 # 把当前点置为1 stack.append((i + di, j + dj)) # 把当前的位置添加到栈里面 break else: # 如果所有的点都不可走 stack.pop() # 退回上一步 return stack # 如果迷宫不能走则返回空栈 Maze = initMaze() # 初始化迷宫 result = path(maze=Maze, start=(1, 1), end=(5, 5)) # 老鼠开始走迷宫 print(result) # [(1, 1), (1, 2), (2, 2), (3, 2), (3, 1), (4, 1), (5, 1), (5, 2), (5, 3), (4, 3), (4, 4), (4, 5), (5, 5)]
 問題
問題
10kgのアイテムを収納できるバックパックがあります。 現在6つのアイテムがあります:
アイテム1 +など、バックパックを満たすことができるすべての解決策を書いて見つけてください。項目5。 コードの解決策#!/use/bin/env python
# _*_ coding:utf-8 _*_
operators = { # 运算符操作表
'+': lambda op1, op2: op1 + op2,
'-': lambda op1, op2: op1 - op2,
'*': lambda op1, op2: op1 * op2,
'/': lambda op1, op2: op1 / op2,
}
def evalPostfix(e):
"""
:param e: 后缀表达式
:return: 正常情况下栈内的第一个元素就是计算好之后的值
"""
tokens = e.split() # 把传过来的后缀表达式切分成列表
stack = []
for token in tokens: # 迭代列表中的元素
if token.isdigit(): # 如果当前元素是数字
stack.append(int(token)) # 就追加到栈里边
elif token in operators.keys(): # 如果当前元素是操作符
f = operators[token] # 获取运算符操作表中对应的lambda表达式
op2 = stack.pop() # 根据先进后出的原则,先让第二个元素出栈
op1 = stack.pop() # 在让第一个元素出栈
stack.append(f(op1, op2)) # 把计算的结果在放入到栈内
return stack.pop() # 返回栈内的第一个元素
result = evalPostfix('2 3 4 * +')
print(result)
# 14以上がこの記事の全内容です。この記事の内容が皆さんの勉強や仕事に少しでもお役に立てれば幸いです。ご不明な点がございましたら、お気軽にお問い合わせください。伝えるためのメッセージ。
Python アルゴリズム アプリケーション スタックの詳細な説明については、PHP 中国語 Web サイトに注目してください。