
PHP の無限分類では再帰的な手法が多く使われていますが、再帰についての理解はまだ曖昧です。次に、誰もが包括的に理解できるように、再帰の長所と短所について詳しく理解します。
再帰とは何ですか?
定義
再帰(英語: Recursion )は、数学やコンピュータサイエンスにおいて、再帰とも訳され、関数の定義において関数そのものを利用する手法を指す。
英語のRecursionの語源分析は、単に「re-(再び)」+「curs-(来る、起こる)」であり、再発、再出現を意味します。 対応する中国語訳「回帰」は、「再帰」+「回帰」の 2 つの意味を表します。 この 2 つの意味が再帰的思考の本質です。この観点からすると、中国語訳の方が表現力が豊かです。
私はインターネットでこの比喩を何度も見ました:
あなたが映画館にいて、自分がどの列に座っているのか知りたいとしますが、あなたの前にはたくさんの人がいて、あなたも同じです数えるのが面倒なので、前の列に「どの列に座っていますか?」と尋ねると、前の人 (コードネーム A) が答えた後、自分がどの列にいるかがわかります。A の答えに 1 を加えるだけです。 , あなたがいる列になります。案外、Aさんはあなたより怠け者で、数えるのが嫌なので、自分が何列目にいるのかわかるように、目の前にいるBさんにも「何列に座っていますか?」と尋ねます。あなたと同じ手順を使用して。次にBも同じことをします。グループが最前列について質問するまで、最前列の人は質問者に「私は最前列です」と伝えました。ようやく全員が自分がどの列にいるのかを知ることができます。 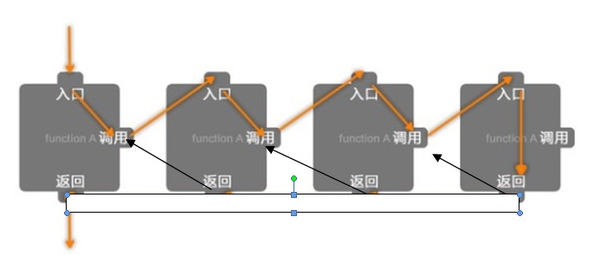
とループ
の違い 上記のwikiの定義を見る限り、通常無限ループと呼ばれるものと非常に似ているように見えますが、両者の違いは何でしょうか。 ?
再帰とは、静止した状態での移動であり、行ったり来たりすることです。
そのサイクルは同じ動きと静止であり、戻ることはありません。
たとえば、鍵を渡され、ドアの前に立って、この鍵で何つのドアを開けることができるかを尋ねます。
反復: 目の前のドアを開けると、家の中に別のドアが見えます (このドアは、前に開いたドアと同じサイズである可能性があります (静か)、または小さい可能性があります (動いている))、あなたはその上を歩きますそして、手に持った鍵でまだ開くことができます。ドアを押して開けると、中には別のドアがあることが分かります。 。 。 , 何度か繰り返した後、目の前のドアを開けると、部屋は 1 つだけでドアがありません。 同じように歩き始めて、部屋に戻るたびに、入り口に着いたら、この鍵で何回ドアを開けたかを数えます。
ループ: 目の前のドアを開けると、家の中に別のドアが見えます (このドアは、前に開いたドアと同じサイズである場合もあります (静か)、または小さい場合もあります (動いている))、あなたは歩きます手に持った鍵でまだ開くことができることに気づき、ドアを押し開けると、中には別のドアがあることがわかります(前のドアが同じであれば、このドアも同じです。2 番目のドアであれば。 1 番目のドアよりも小さい場合、このドアも同じになります。) 2 番目のドアよりも小さい (動きは同じ、変化なしまたは同じ変化))、このドアを開け続けます。 。 。 、このまま続けてください。 入り口にいる人は、あなたが戻ってきて答えを教えてくれるのを決して待ちません。
再帰的思考
再帰とは、行く(行く)と戻る(戻る)という意味です。
具体的には、なぜ「行ける」のでしょうか?
再帰を必要とするこの問題では、同じ問題解決のアイデアを使用して、似ているがわずかに異なる質問に答えることができる必要があります (上の例の鍵は裏口の鍵を開けることができます)。
なぜ「戻る」ことができるのですか?
これには、これらの問題が大きいものから小さいもの、近いものから遠いものへと成長し続けるにつれて、終点、臨界点、ベースラインが存在し、その点に到達すると、より小さなものやより小さなものに進む必要がなくなることが必要です。さらに遠くの点に移動し、その点から開始して元の点に戻ります。
再帰の基本的な考え方は、大規模な問題を小規模な同様のサブ問題に変換して解決することです。関数を実装する場合、大きな問題を解決する方法と小さな問題を解決する方法は同じであることが多いため、関数はそれ自体を呼び出します。さらに、無限再帰が発生しないように、問題を解決する関数には明確な終了条件が必要です。
再帰を使用する必要があるのはどのような場合ですか?
いくつかの問題の定義自体が再帰形式である場合、それを解決するために再帰を使用するのが最も適しています。
「ツリー」の定義は、コンピューター サイエンスを専攻する学生に最もよく知られています [4,5]。階乗、フィボナッチ数列 [6] などのいくつかの定義もあります。再帰を使用してこれらの問題を解決すると、多くの場合、わずか数行のコードで一見「恐ろしい」問題が解決されます。 もちろん、再帰的なパフォーマンスの問題は、特定のエンジニアリングの実践においては、スタック割り当てと関数呼び出しのコストを考慮する必要があります。 しかし、今、再帰的思考についてのみ議論しているのであれば、それらのことは脇に置いて、再帰の美しさを理解したほうがよいでしょう。
再帰は、特定の問題を解決するときの考え方を簡素化し、コードがより洗練されて読みやすくなります。では、再帰には非常に多くの利点があるため、すべての問題を解決するために再帰を使用する必要があるのでしょうか?再帰にはデメリットはないのでしょうか?今日は再帰の欠点について説明します。再帰に関しては、効率の問題に直面しなければなりません。
なぜ再帰は非効率なのでしょうか?
フィボナッチ数列を例にしてみましょう。再帰や計算の複雑さについて言及する多くの教科書や記事では、フィボナッチ数列を計算するプログラムが典型的な例として使用されます。 C# でフィボナッチ数列の n 番目の数をできるだけ早く計算する関数を作成するように求められた場合 (1 未満のパラメーターや結果のオーバーフローなどの例外に関係なく)、あなたのプログラムがこの条件に一致するかどうかはわかりません。次のコードは次のとおりです:
public static ulong Fib(ulong n)
{
return (n == 1 || n == 2) ? 1 : Fib(n - 1) + Fib(n - 2);
}このコードは、短くて簡潔 (実行コードは 1 行のみ)、直観的かつ明確で、多くのプログラマーのコードの美学と非常に一致していると考える必要があります。面接中にそのようなコードを書きます。しかし、このコードを使って Fib(1000) を計算しようとすると、その実行時間に気が狂ってしまうかもしれません。
プログラムの効率性が受け入れられない場合、見た目の良いコードは役に立たない可能性があるようです。プログラムの実行フローを簡単に分析すると、Fibonacci(5) の計算を例にとります。
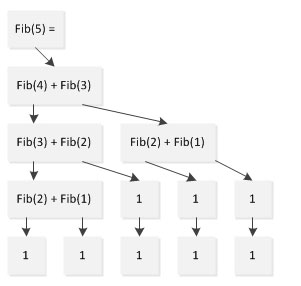
上の図からわかるように、Fib( 5)、Fib(1)は2回、Fib(2)は3回、Fib(3)は2回計算され、わずか5回の計算で完了するタスクが9回計算された。この問題はスケールが大きくなるにつれてますます顕著になり、Fib(1000) を許容可能な時間内に計算できなくなります。
私たちは fib(n) を見つけるために単純な定義を使用していました。つまり、式 fib(n) = fib(n-1) + fib(n-2) を使用していました。この考えは簡単に思いつきますが、注意深く分析すると、 fib(n-1) が呼び出されるときに fib(n-2) も呼び出され、つまり fib(n-2) が 2 回呼び出されることになります。同様に、f(n-2) が呼び出されるときに f(n-3) も 2 回呼び出され、これらの冗長な呼び出しはまったく不要です。このアルゴリズムの複雑さは指数関数的であると計算できます。
改善されたフィボナッチ再帰アルゴリズム
では、フィボナッチ数列を計算するためのより優れた再帰アルゴリズムはあるのでしょうか? もちろんあります。フィボナッチ数列の最初のいくつかの項目を見てみましょう:
11、1、2、3、5、8、13、21、34、55...
前の項目を削除すると、得られたシーケンスは依然として f(n) = f(n-1) – f(n-2)、(n>2) を満たしており、取得したシーケンスは 1 と 2 から始まります。このシーケンスの n-1 番目の項目が元のシーケンスの n 番目の項目であることは簡単にわかります。どうですか、アルゴリズムをどのように設計すればよいかわかりますか?このような関数を作成すると、3 つのパラメーターを受け取ります。最初の 2 つはシーケンスの最初の 2 つの項目で、3 番目は最初の 2 つのパラメーターから始まる検索するシーケンスの番号です。
1int fib_i(int a, int b, int n);
関数内では、まず n の値を確認します。n が 3 の場合、これは単純な状況です。 n>3 の場合、f(b, a+b, n-1) を呼び出します。これにより、問題のサイズが縮小されます (n 番目の項の検索から n-1 番目の項の検索まで)。最終的なコードは次のとおりです:
int fib_i(int a, int b , int n)
{
if(n == 3)
return a+b;
else
return fib_i(b, a+b, n-1);
}メモリに大きなオーバーヘッドがあるのはなぜですか?
再帰の原理は、まず計算対象の変数値をスタックに格納し、その後再帰終了条件が満たされるまで順番にループし、その後計算対象の変数値をスタックから取得して最終結果を計算します。
例え: 10 を計算してください! =
再帰の場合、プロセスは次のとおりです: 10! =10 * 9!
9!=9 * 8!
…
2! =2*1!
1! =1
計算するとき、再帰条件が 1 を満たすまで式を 1 つずつメモリに保存します。 =1 に設定し、メモリから保存したばかりの式を取得して最終結果を取得します。この場合、より多くのシステム リソースが消費されます。
そして、システムは最大再帰深さを設定します。この深さよりも大きい場合は、エラーが報告されて終了します。関数の再帰呼び出し中、関数内のパラメーター、戻り値などが継続的にスタックにプッシュされます。関数呼び出しは常にスタックを使用し、シーンにレポートし、シーンを復元するため、メモリのオーバーヘッドはますます大きくなります。ただし、PHP には末尾再帰に対する最適化効果がないため、この解決策は役に立ちません。実用的な意味。