Photoshop スタイルの角度と高さのセレクター コントロール

はじめに
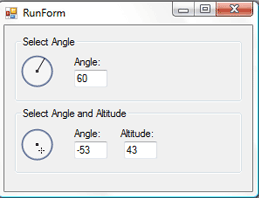
Adobe Photoshop には、投影、ベベル、エンボスなどの特殊効果を設定するための 2 つの非常に専門的なコントロールがあります。1 つは角度セレクターで、もう 1 つは角度と高さのセレクターです (図を参照)上記のショー)。
この記事では、Photoshop でこれら 2 つのコントロールの外観と動作を模倣する 2 つのカスタム コントロールを作成する方法を読者に紹介します。
基礎知識 - 数学
三平方の定理
(原文尊重のため三平方の定理、以下三平方の定理と呼びます。少し複雑ですが。 - のびのメモ)
三平方の定理を使うと、直角三角形の斜辺(最長の辺)。計算式は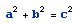 です。このように、斜辺 c は
です。このように、斜辺 c は  に等しくなります。
に等しくなります。
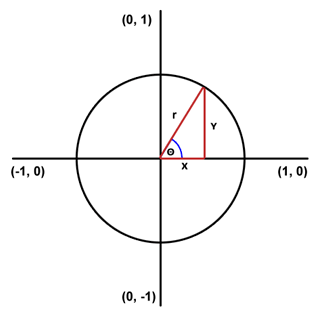
単位円
次の作業は角度と円に関連するため、最初に単位円の形に慣れておくと役立ちます。単位円は中心(0,0)、半径1の円です。規則的なグリッド (キャンバスを参照 - Nobi のメモ) では、0 度 (座標) は点 (1,0) (右) から始まり、反時計回りに増加します。したがって、90 度は (0,1)、180 度は (-1,0)、270 度は (0,-1)、そして最後に 360 度が 0 点と一致します。
三角関数
ここでは、sin、cos、tanの3つの基本的な三角関数を知っていれば十分です(サイン、コサイン、タンジェント - のびノート)。 SOH-CAH-TOA (注釈 +) を覚えていると、(直角) 三角形のサインは斜辺に対する反対側の辺の比に等しく、コサインは隣接する辺の比に等しいことがわかります。斜辺に対する接線は、反対側と隣接する側の比に等しくなります。
同様に、逆三角関数は未知の角度を計算するために使用されることがわかっています。
翻訳注+:
SOH-CAH-TOA は、外国人が三角関数を暗記するために使用する公式です。このうち、Oは反対側(反対側)、Hは斜辺(斜辺)、Aは隣接側です。
SOH: Sine = Opposite ÷ Hypotenuse
CAH: Cosine = Adjacent ÷ Hypotenuse
TOA: Tangent = Opposite ÷ Hypotenuse
共通関数
以下の 2 つの重要な関数は、私たちが作成するカスタム コントロール ( メソッド ) で使用されます。 :
角度と半径をパラメータとして受け取り、ある原点の周りの対応する点の位置を返す関数。 (簡単に言うと、角度を点に変換することです)
点(X,Y)をパラメータとして、その逆を完成させて、最もよく一致する角度を見つける関数です。
最初の関数はより単純です:
private PointF DegreesToXY(float degrees, float radius, Point origin)
{
PointF xy = new PointF();
double radians = degrees * Math.PI / 180.0;
xy.X = (float)Math.Cos(radians) * radius + origin.X;
xy.Y = (float)Math.Sin(-radians) * radius + origin.Y;
return xy;
}最初に角度をラジアンに変換する必要があることに注意してください。一般的に言えば、単位円内で勉強するだけで済みます。
この関数は、既知の角度と半径を持ち、三角関数を使用して X 値と Y 値を計算し、指定された原点の初期座標を加算します。
関数コードで Y コンポーネントの負の値が使用されていることにも注意してください。これは、コンピューターのモニター上のグリッドが逆さまになっているためです (下が正です)。
2 番目の関数の機能は、ユーザーがコントロール上でクリックしたポイントの位置を、対応する角度値に変換することです。いくつかのことを追加することを考慮する必要があるため、これは少し難しくなります。記事の長さに制限があるため、コードの一部をここに掲載します:
private float XYToDegrees(Point xy, Point origin)
{
double angle = 0.0;
if (xy.Y < origin.Y)
{
if (xy.X > origin.X)
{
angle = (double)(xy.X - origin.X) / (double)(origin.Y - xy.Y);
angle = Math.Atan(angle);
angle = 90.0 - angle * 180.0 / Math.PI;
}
else if (xy.X < origin.X)
{
//如此这般
}
}
else if (xy.Y > origin.Y)
{
//如此这般
}
if (angle > 180) angle -= 360; //控制角度范围
return (float)angle;
}この関数は主に、中心点に対する相対的な位置をチェックすることによってマウスの象限を決定します。象限がわかれば、三角関数 (逆正接) を使用して角度を計算できます。
角度が 180 度より大きい場合は、360 度を減算します。これは Photoshop と同様に、-180 度から 180 度の間で角度を制御します。もちろん、この手順を実行する必要はありません。このコード行を追加しなくてもコントロールは使用できます。
コントロールを作成します
コントロールを描画します
2つのコントロールは同じ背景を持ちます:
幅2のペンで外側の円を描きます
40%(約100%)の白で塗りつぶします) 不透明度
コントロールの中心は 3x3 ピクセルの正方形です
protected override void OnPaint(PaintEventArgs e)
{
//...
//Draw
g.SmoothingMode = SmoothingMode.AntiAlias;
g.DrawEllipse(outline, drawRegion);
g.FillEllipse(fill, drawRegion);
//...光标
g.SmoothingMode = SmoothingMode.HighSpeed;
g.FillRectangle(Brushes.Black, originSquare);
//...
}注意SmoothMode属性。在绘制圆圈时将该属性设置为AntiAlias(抗锯齿),这样看起来既光滑又专业。但是如果画正方形时也用抗锯齿,就会显得模糊难看,所以将SmoothMode设置为HighSpeed(高速),这样画出的正方形边缘整齐犀利。
根据控件不同,光标也有不同绘制方法。角度选择器比较简单,只需要从圆心到DegreesToXY函数返回的点连一条直线即可。角度与高度选择器则是在这点上绘制一个1x1的矩形,然后在周围绘制一个十字型光标。
处理用户点击
多亏我们有了XYToDegrees函数,处理用户点击变得特别简单。为了让我们的控件用起来和Photoshop一模一样,我们需要设置MouseDown和MouseMove事件。这样,各项数值将实时更新。这里是一个附注函数的代码:
private int findNearestAngle(Point mouseXY)
{
int thisAngle = (int)XYToDegrees(mouseXY, origin);
if (thisAngle != 0)
return thisAngle;
else
return -1;
}高度控件需要额外的处理,就是找到中心点和鼠标点击点的距离:
private int findAltitude(Point mouseXY)
{
float distance = getDistance(mouseXY, origin);
int alt = 90 - (int)(90.0f * (distance / origin.X));
if (alt < 0) alt = 0;
return alt;
}在Photoshop中,选择点(指鼠标点击点)在圆心时,高度为90,在边缘处则为0。这样,我们可以通过找到点击点到圆心距离和半径高度比值来计算出高度。然后,用90减去该值(实际上是按90到0来翻转一下)。
自定义事件
为了让我们的自定义控件更加专业,需要控件能够在数值发生变化时以编程方式进行提醒。这就是我们要设置事件的原因。
例如,像这样给角度变化添加一个事件:
public delegate void AngleChangedDelegate(); public event AngleChangedDelegate AngleChanged;
然后,我们要做的就是每次变更Angle属性时,调用AngleChanged()(需要先判断是否为null)。
限制与改进
闪烁
没有闪烁!只需要在制作控件时设置DoubleBuffered属性为true,.NET Framework 2.0会处理剩下的工作,保证控件能流畅的重绘。
尺寸
因为控件使用基于半径(圆)的数学计算方法,因此需要保证控件的长度和宽度相等。
颜色
我是照着Photoshop的样子来的,所以并没包含背景颜色、外圈颜色这些属性。但是,浏览下代码,你会发现改成你喜欢的颜色或者让颜色可以动态修改并不是什么难事。
结论
我建议你下载项目文件(或者至少下载DEMO),这样你可以看到这俩控件用起来很爽。
协议
本文及有关代码、程序均基于CPOL(Codeproject Open License)协议。
更多Photoshop样式的角度和高度选择器控件 相关文章请关注PHP中文网!

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7643
7643
 15
15
 1392
1392
 52
52
 91
91
 11
11
 33
33
 151
151
 PSが荷重を見せ続ける理由は何ですか?
Apr 06, 2025 pm 06:39 PM
PSが荷重を見せ続ける理由は何ですか?
Apr 06, 2025 pm 06:39 PM
PSの「読み込み」の問題は、リソースアクセスまたは処理の問題によって引き起こされます。ハードディスクの読み取り速度は遅いか悪いです。CrystaldiskInfoを使用して、ハードディスクの健康を確認し、問題のあるハードディスクを置き換えます。不十分なメモリ:高解像度の画像と複雑な層処理に対するPSのニーズを満たすためのメモリをアップグレードします。グラフィックカードドライバーは時代遅れまたは破損しています:ドライバーを更新して、PSとグラフィックスカードの間の通信を最適化します。ファイルパスが長すぎるか、ファイル名に特殊文字があります。短いパスを使用して特殊文字を避けます。 PS独自の問題:PSインストーラーを再インストールまたは修理します。
 PSでPDFをエクスポートすることに関する一般的な質問は何ですか
Apr 06, 2025 pm 04:51 PM
PSでPDFをエクスポートすることに関する一般的な質問は何ですか
Apr 06, 2025 pm 04:51 PM
PSをPDFとしてエクスポートする際のよくある質問とソリューション:フォント埋め込み問題:「フォント」オプションを確認し、「埋め込み」を選択するか、フォントを曲線(パス)に変換します。色偏差の問題:ファイルをCMYKモードに変換し、色を調整します。 RGBで直接エクスポートするには、プレビューと色の逸脱のための心理的な準備が必要です。解像度とファイルサイズの問題:実際の条件に応じて解像度を選択するか、圧縮オプションを使用してファイルサイズを最適化します。特殊効果の問題:エクスポートする前にレイヤーをマージ(フラットン)するか、長所と短所を比較検討します。
 PSが常にロードされていることを常に示しているときに、ロードの問題を解決する方法は?
Apr 06, 2025 pm 06:30 PM
PSが常にロードされていることを常に示しているときに、ロードの問題を解決する方法は?
Apr 06, 2025 pm 06:30 PM
PSカードは「ロード」ですか?ソリューションには、コンピューターの構成(メモリ、ハードディスク、プロセッサ)の確認、ハードディスクの断片化のクリーニング、グラフィックカードドライバーの更新、PS設定の調整、PSの再インストール、優れたプログラミング習慣の開発が含まれます。
 PSの負荷速度をスピードアップする方法は?
Apr 06, 2025 pm 06:27 PM
PSの負荷速度をスピードアップする方法は?
Apr 06, 2025 pm 06:27 PM
Slow Photoshopの起動の問題を解決するには、次のような多面的なアプローチが必要です。ハードウェアのアップグレード(メモリ、ソリッドステートドライブ、CPU)。時代遅れまたは互換性のないプラグインのアンインストール。システムのゴミと過剰な背景プログラムを定期的にクリーンアップします。無関係なプログラムを慎重に閉鎖する。起動中に多数のファイルを開くことを避けます。
 PSのエクスポートPDFのパスワード保護を設定する方法
Apr 06, 2025 pm 04:45 PM
PSのエクスポートPDFのパスワード保護を設定する方法
Apr 06, 2025 pm 04:45 PM
Photoshopでパスワードで保護されたPDFをエクスポート:画像ファイルを開きます。 [ファイル]&gtをクリックします。 「エクスポート」&gt; 「PDFとしてのエクスポート」。 「セキュリティ」オプションを設定し、同じパスワードを2回入力します。 [エクスポート]をクリックして、PDFファイルを生成します。
 PSペンツールの使用方法
Apr 06, 2025 pm 10:15 PM
PSペンツールの使用方法
Apr 06, 2025 pm 10:15 PM
ペンツールは、正確なパスと形状を作成するツールであり、次のように使用されます。ペンツール(P)を選択します。パス、充填、ストローク、および形状オプションを設定します。 [アンカーポイントの作成]をクリックし、曲線をドラッグして[アンカーポイントの作成]を解除します。 CTRL/CMD ALT/OPTを押して、アンカーポイントを削除し、アンカーポイントをドラッグして移動し、[曲線を調整]をクリックします。最初のアンカーをクリックしてパスを閉じて形状を作成し、最後のアンカーをダブルクリックして開いたパスを作成します。
 遅いPSの読み込みはコンピューター構成に関連していますか?
Apr 06, 2025 pm 06:24 PM
遅いPSの読み込みはコンピューター構成に関連していますか?
Apr 06, 2025 pm 06:24 PM
PSの負荷が遅い理由は、ハードウェア(CPU、メモリ、ハードディスク、グラフィックスカード)とソフトウェア(システム、バックグラウンドプログラム)の影響を組み合わせたものです。ソリューションには、ハードウェアのアップグレード(特にソリッドステートドライブの交換)、ソフトウェアの最適化(システムガベージのクリーンアップ、ドライバーの更新、PS設定のチェック)、およびPSファイルの処理が含まれます。定期的なコンピューターのメンテナンスは、PSのランニング速度を改善するのにも役立ちます。
 PSがファイルを開いたときにロードの問題を解決する方法は?
Apr 06, 2025 pm 06:33 PM
PSがファイルを開いたときにロードの問題を解決する方法は?
Apr 06, 2025 pm 06:33 PM
「ロード」は、PSでファイルを開くときに発生します。理由には、ファイルが大きすぎるか破損しているか、メモリが不十分で、ハードディスクの速度が遅い、グラフィックカードドライバーの問題、PSバージョンまたはプラグインの競合が含まれます。ソリューションは、ファイルのサイズと整合性を確認し、メモリの増加、ハードディスクのアップグレード、グラフィックカードドライバーの更新、不審なプラグインをアンインストールまたは無効にし、PSを再インストールします。この問題は、PSパフォーマンス設定を徐々にチェックして使用し、優れたファイル管理習慣を開発することにより、効果的に解決できます。




