Photoshopガウスぼかしフィルターのアルゴリズムまとめ-PS チュートリアル-php.cn

ホームページ

ウェブフロントエンド

PS チュートリアル

Photoshopガウスぼかしフィルターのアルゴリズムまとめ

高洛峰

Feb 20, 2017 am 09:40 AM

网最近、一部のネットユーザーがガウス曖昧フィルターについて研究していると感じました。要約は次のとおりです。ガウスぼかしは、デジタル画像テンプレート処理法の一種です。そのテンプレートは、2次元の正規分布(ガウス分布)関数に基づいて計算されます。正の分布は、A. 棣 Morf によって、2 つのアイテムが分布する近似式で最初に得られました。 C.F. ガウスは、測定誤差を研究する際に別の角度からそれを導き出しました。 P.S. ラプラスとガウスはその性質を研究しました。したがって、ガウスぼかしという名前が付けられます。 1 次元分布関数の定義:

タイプの確率変数の分布。最初のパラメーター μ は正規分布に従う確率変数の平均値です。2 番目のパラメーター σ2 はこの確率変数の分散です。 , したがって、正規分布は N(μ, σ2) と表されます。正規分布に従う確率変数の確率則は、μ に近い値を取る確率が高く、μ から遠い値を取る確率が小さくなるというもので、σ が小さいほど分布が集中します。はμに近く、σが大きいほど分散は小さくなります。正規分布の密度関数の特徴は、μに対して対称であり、μで最大値をとり、正（負）の無限大で値が０となり、μ±σで変曲点をもつことである。形状は中央が高く、両側が低く、x 軸より上の釣鐘型の曲線になります。 μ = 0、σ2 = 1 の場合、それは標準正規分布と呼ばれ、N (0, 1) として記録されます。

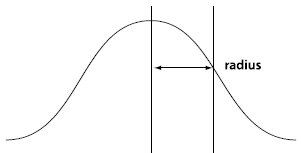
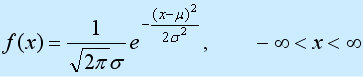Photoshopガウスぼかしフィルターのアルゴリズムまとめ 2 つの定数の意味: μ-期待値、σ^2 分散。 ashing最初の質問を解決しましょう：ガウスブルールフィルターの半径は何ですか？答えは、ガウス半径が式の σ であるということです。 σを使用して、曲線が大きく、σが大きくなり、曲線が大きくなり、垂れ下がっています。 2 次元画像の場合、ガウス半径が小さいほど、表面は高く、より鋭くなり、より急になります。ガウス半径が大きいほど、表面はより低く、より緩やかになります。したがって、ガウス半径が小さいほどブラーは小さくなり、ガウス半径が大きいほどブラーは大きくなります。 ps がガウス半径の範囲を [0.1~250] として定義していることがわかります。半径が 0.1 の場合、ガウステンプレートの中央のピクセルだけが計算後に 1 になり、他のピクセルはすべて = 0 (実際には 0 に近づくだけ)、つまり画像は変化しません。

2 番目の質問は、ガウステンプレートのサイズとガウス半径の関係は何ですか?これは常に私たちを悩ませてきた誤解です。それは、私たちの思考が物理的な実現についての誤解に入ってしまっているからです。物理的な実装では、ガウステンプレートは制限されているため、この質問に対する実際の答えが無視されます。つまり、ガウステンプレートは論理的に制限がありません。つまり、ガウステンプレートは本質的に、論理的に無限に拡張された表面の近似です。したがって、テンプレートのサイズは無限であると考える必要があります。計算中に、距離が 0 に近づくため、特定のしきい値を下回るこれらの値はテンプレートの境界とはみなされなくなります。以下、二次元ガウス曲面の式(x,yはピクセルのテンプレート座標を表し、テンプレートの中心位置が原点となる):

Photoshopガウスぼかしフィルターのアルゴリズムまとめ

: G ( x, y) = (1 / (2 (2 2 (2 2 *pi*σ^2) ) * exp( -(x^2+y^2)/(2*σ^2) ) ;

によるとこの式に従うと、さまざまな半径の下でガウステンプレートを計算できます。実際、テンプレートは無限ですが、中心から遠く離れると 0 に近づきます。たとえば、r=0.7 の場合に正規化されたガウステンプレートを計算します。

ガウステンプレート (guass radius=0.700000)

在网络上众周知流传的高斯3*3模板实际上是对高斯曲面の一整数除法形式の近似:

1 2 1

2 4 2 /16

1 2 1

実際に検証したところ、この 3*3 テンプレートは実際には約 0.849 のガウス半径に似ていることがわかりました。R = 0.849 の場合、3*3 はテンプレートです (MATLAB では

H = FSPECIAL ( 'gaussian) ', 3, 0.849);このテンプレートを入手できます):

0.125000 0.250131 0.125000 0.062467 0.125000 0.062467

次に、画像内で Matlab imfilter を使用してガウスぼかしを処理できます。

g、h）;効果は次のとおりです。

Actiphighlight (FreeWare) によって作成されたコードハイライト http:// www.php.cn/

-->
%
ガウスぼやけた表面を描画します! ---------------------r

0.849

;

Photoshopガウスぼかしフィルターのアルゴリズムまとめ %

ガウス半径 (0.1 から 250)

using using through using ' s ' through ' s ' through using using 's ‐ ‐ ‐d ‐ to generated a Gaussian Blur Filter in Matlab 関連記事については、PHP 中国語 Web サイトに注目してください。

このウェブサイトの声明

この記事の内容はネチズンが自主的に寄稿したものであり、著作権は原著者に帰属します。このサイトは、それに相当する法的責任を負いません。盗作または侵害の疑いのあるコンテンツを見つけた場合は、admin@php.cn までご連絡ください。