Python ソート アルゴリズムの概要と例
この記事では主にPythonのソートアルゴリズムの概要と詳細な例に関する関連情報を紹介しますので、必要な方は参考にしてください
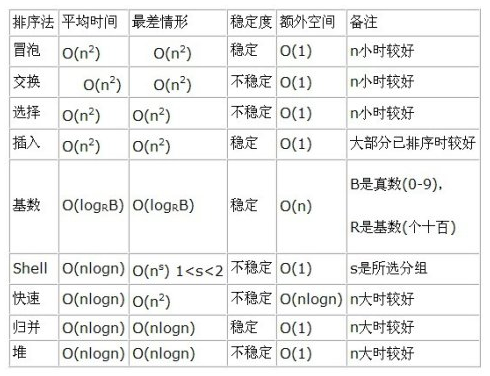
一般的な集中ソートアルゴリズムの概要
マージソート
とも呼ばれます。マージ ソートは、分割統治法の典型的な応用例です。分割統治の考え方は、それぞれの問題を小さな問題に分解し、それぞれの小さな問題を解決してから、それらを統合することです。
具体的なマージソートは、順序付けされていない数値のセットを n/2 ずつ 1 つの要素だけを持つサブ項目に再帰的に分解することであり、1 つの要素はすでにソートされています。次に、これらの順序付けされたサブ要素をマージします。
マージのプロセスは、ソートされた 2 つのサブシーケンスを比較し、最初に 2 つのサブシーケンスの最小の要素を選択し、2 つの要素の最小のサブシーケンスを選択し、それをサブシーケンスから削除して最終結果セットに追加します
。サブシーケンスはマージされます。
コードは次のとおりです:
#!/usr/bin/python
import sys
def merge(nums, first, middle, last):
''''' merge '''
# 切片边界,左闭右开并且是了0为开始
lnums = nums[first:middle+1]
rnums = nums[middle+1:last+1]
lnums.append(sys.maxint)
rnums.append(sys.maxint)
l = 0
r = 0
for i in range(first, last+1):
if lnums[l] < rnums[r]:
nums[i] = lnums[l]
l+=1
else:
nums[i] = rnums[r]
r+=1
def merge_sort(nums, first, last):
''''' merge sort
merge_sort函数中传递的是下标,不是元素个数
'''
if first < last:
middle = (first + last)/2
merge_sort(nums, first, middle)
merge_sort(nums, middle+1, last)
merge(nums, first, middle,last)
if __name__ == '__main__':
nums = [10,8,4,-1,2,6,7,3]
print 'nums is:', nums
merge_sort(nums, 0, 7)
print 'merge sort:', nums安定、時間計算量 O(nlog n)
挿入ソート
コードは次のとおりです:
#!/usr/bin/python
importsys
definsert_sort(a):
''''' 插入排序
有一个已经有序的数据序列,要求在这个已经排好的数据序列中插入一个数,
但要求插入后此数据序列仍然有序。刚开始 一个元素显然有序,然后插入一
个元素到适当位置,然后再插入第三个元素,依次类推
'''
a_len = len(a)
if a_len = 0 and a[j] > key:
a[j+1] = a[j]
j-=1
a[j+1] = key
return a
if __name__ == '__main__':
nums = [10,8,4,-1,2,6,7,3]
print 'nums is:', nums
insert_sort(nums)
print 'insert sort:', nums安定、時間計算量O(n^ 2)
Pythonで2つの要素の値を交換するには、a, b = b, aと書くことができます。実は、これは代入記号の左側と右側がタプルだからです
。(Python ではタプルは実際には括弧ではなくカンマ「,」で区切られることをここで強調する必要があります)。
選択ソート
選択ソートは、シンプルで直感的な並べ替えアルゴリズムです。仕組みは次のとおりです。まず、ソートされていないシーケンス内で最小の (大きい) 要素を見つけて、ソートされたシーケンスの先頭に格納します。次に、ソートされていない残りの要素から最小の (大きい) 要素を見つけて、それをソートされたシーケンスの最後に置きます。ソートされたシーケンス。すべての要素がソートされるまで続きます。
import sys
def select_sort(a):
''''' 选择排序
每一趟从待排序的数据元素中选出最小(或最大)的一个元素,
顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完。
选择排序是不稳定的排序方法。
'''
a_len=len(a)
for i in range(a_len):#在0-n-1上依次选择相应大小的元素
min_index = i#记录最小元素的下标
for j in range(i+1, a_len):#查找最小值
if(a[j]<a[min_index]):
min_index=j
if min_index != i:#找到最小元素进行交换
a[i],a[min_index] = a[min_index],a[i]
if __name__ == '__main__':
A = [10, -3, 5, 7, 1, 3, 7]
print 'Before sort:',A
select_sort(A)
print 'After sort:',A不安定、時間計算量 O(n^2)
ヒル ソートヒル ソート、降順増分ソート アルゴリズムとも呼ばれるヒル ソートは、非安定なソート アルゴリズムです。この方法は、DL であるため、増分ソートの削減とも呼ばれます。シェルは 1959 年に提案されたことにちなんで名付けられました。
まず最初の増分として n より小さい整数 d1 をとり、ファイル内のすべてのレコードを d1 グループに分割します。距離が d1 の倍数であるすべてのレコードは、同じグループに配置されます。各グループ内で最初にソートします
次に、2番目の増分を取得します
import sys
def shell_sort(a):
''''' shell排序
'''
a_len=len(a)
gap=a_len/2#增量
while gap>0:
for i in range(a_len):#对同一个组进行选择排序
m=i
j=i+1
while j<a_len:
if a[j]<a[m]:
m=j
j+=gap#j增加gap
if m!=i:
a[m],a[i]=a[i],a[m]
gap/=2
if __name__ == '__main__':
A = [10, -3, 5, 7, 1, 3, 7]
print 'Before sort:',A
shell_sort(A)
print 'After sort:',A不安定、時間計算量は平均時間O(nlogn)、最悪時間O(n^s)1です
ヒープソート
「ヒープ」の定義: 開始インデックスが 0 の「ヒープ」内:
ノード i の右側の子ノードは位置 2 * i + 24) にありますノード i の親ノードは位置 Floor( ( i – 1) / 2) : フロアは「丸め」操作を表すことに注意してください
ヒープの特性:
各ノードのキー値は常に親ノードより大きい (または小さい) 必要があります
" "最大ヒープ":
「ヒープ」のルートノードは、最大のキー値を持つノードを保存します。つまり、「ヒープ」内の各ノードのキー値は、常にその子ノードよりも大きくなります。
上に移動、下に移動:
ノードのキー値が親ノードより大きい場合、「上に移動」操作を実行する必要があります。つまり、ノードを親ノードの位置に移動します。 、親ノードがその位置に到達するようにしてから、ノードの判断を続け、ノードが親ノードより大きくなくなるまで「上への移動」を停止しません。
ここで、「下に移動」操作について詳しく学びましょう。ノードのキー値をより小さい値に変更する場合は、「下に移動」する必要があります。
方法:
最初に最大のヒープ (時間計算量 O(n)) を構築し、その後毎回、ルート ノードを最後の位置のノードと交換するだけで済み、その後、最後の位置を除外し、交換後、ルート ノードのヒープが調整されます (時間計算量 O(lgn))。つまり、ルート ノードを「下に移動」できます。 ヒープソートの合計時間計算量は O(nlgn) です。 コードは次のとおりです:
#!/usr/bin env python
# 数组编号从 0开始
def left(i):
return 2*i +1
def right(i):
return 2*i+2
#保持最大堆性质 使以i为根的子树成为最大堆
def max_heapify(A, i, heap_size):
if heap_size <= 0:
return
l = left(i)
r = right(i)
largest = i # 选出子节点中较大的节点
if l A[largest]:
largest = l
if r A[largest]:
largest = r
if i != largest :#说明当前节点不是最大的,下移
A[i], A[largest] = A[largest], A[i] #交换
max_heapify(A, largest, heap_size)#继续追踪下移的点
#print A
# 建堆
def bulid_max_heap(A):
heap_size = len(A)
if heap_size >1:
node = heap_size/2 -1
while node >= 0:
max_heapify(A, node, heap_size)
node -=1
# 堆排序 下标从0开始
def heap_sort(A):
bulid_max_heap(A)
heap_size = len(A)
i = heap_size - 1
while i > 0 :
A[0],A[i] = A[i], A[0] # 堆中的最大值存入数组适当的位置,并且进行交换
heap_size -=1 # heap 大小 递减 1
i -= 1 # 存放堆中最大值的下标递减 1
max_heapify(A, 0, heap_size)
if __name__ == '__main__' :
A = [10, -3, 5, 7, 1, 3, 7]
print 'Before sort:',A
heap_sort(A)
print 'After sort:',A不安定、時間計算量は O(nlog n)
クイックソートクイックソートアルゴリズムとマージ ソート アルゴリズムも分割統治モデルに基づいています。部分配列 A[p…r] を簡単にソートする分割統治プロセスの 3 つのステップは次のとおりです:分解: 配列 A[p…r] を A[p…q-1] と A[q] に分割します。 +1… r] 2 つの部分。A[p...q-1] のすべての要素は A[q] 以下であり、A[q+1...r] のすべての要素は以上です。 A[q] に等しい;
解決策: クイック ソートを再帰的に呼び出して、部分配列 A[p...q-1] と A[q+1...r] を並べ替えます。所定の位置にソートされ、追加の操作は必要ありません。
パーティションの各反復の開始時、任意の配列添字 k に対して、x=A[r] は次のとおりです:
1) p≤k≤i の場合、A[k]≤x。
2) i+1≤k≤j-1 の場合、A[k]>x。
3) k=r の場合、A[k]=x。
コードは次のとおりです:
#!/usr/bin/env python
# 快速排序
'''''
划分 使满足 以A[r]为基准对数组进行一个划分,比A[r]小的放在左边,
比A[r]大的放在右边
快速排序的分治partition过程有两种方法,
一种是上面所述的两个指针索引一前一后逐步向后扫描的方法,
另一种方法是两个指针从首位向中间扫描的方法。
'''
#p,r 是数组A的下标
def partition1(A, p ,r):
'''''
方法一,两个指针索引一前一后逐步向后扫描的方法
'''
x = A[r]
i = p-1
j = p
while j < r:
if A[j] < x:
i +=1
A[i], A[j] = A[j], A[i]
j += 1
A[i+1], A[r] = A[r], A[i+1]
return i+1
def partition2(A, p, r):
'''''
两个指针从首尾向中间扫描的方法
'''
i = p
j = r
x = A[p]
while i = x and i < j:
j -=1
A[i] = A[j]
while A[i]<=x and i < j:
i +=1
A[j] = A[i]
A[i] = x
return i
# quick sort
def quick_sort(A, p, r):
'''''
快速排序的最差时间复杂度为O(n2),平时时间复杂度为O(nlgn)
'''
if p < r:
q = partition2(A, p, r)
quick_sort(A, p, q-1)
quick_sort(A, q+1, r)
if __name__ == '__main__':
A = [5,-4,6,3,7,11,1,2]
print 'Before sort:',A
quick_sort(A, 0, 7)
print 'After sort:',A不安定、最高の時間計算量は O(nlogn)、最悪の時間は O(n^2) です
Python のシーケンスについて話しましょう:
リスト、タプル、文字列はすべてシーケンスですが、シーケンスとは何ですか?そんなに特別なの?シーケンスの 2 つの主な機能は、インデックス演算子とスライス演算子です。インデックス演算子を使用すると、シーケンスから特定の項目を取得できます。スライス演算子を使用すると、シーケンスのスライス、つまりシーケンスの一部を取得できます。たとえば、 a = ['aa','bb','cc']、print a[0] はインデックス演算です。 、スライス操作の場合は a[0:2] を出力します。
この記事を通じてPythonアルゴリズムソートの知識をマスターしたいと思います。このサイトをよろしくお願いします。
Python ソート アルゴリズムの概要と例に関連するその他の記事については、PHP 中国語 Web サイトに注目してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7478
7478
 15
15
 1377
1377
 52
52
 77
77
 11
11
 19
19
 33
33
 LinuxターミナルでPythonバージョンを表示するときに発生する権限の問題を解決する方法は?
Apr 01, 2025 pm 05:09 PM
LinuxターミナルでPythonバージョンを表示するときに発生する権限の問題を解決する方法は?
Apr 01, 2025 pm 05:09 PM
LinuxターミナルでPythonバージョンを表示する際の許可の問題の解決策PythonターミナルでPythonバージョンを表示しようとするとき、Pythonを入力してください...
 あるデータフレームの列全体を、Python内の異なる構造を持つ別のデータフレームに効率的にコピーする方法は?
Apr 01, 2025 pm 11:15 PM
あるデータフレームの列全体を、Python内の異なる構造を持つ別のデータフレームに効率的にコピーする方法は?
Apr 01, 2025 pm 11:15 PM
PythonのPandasライブラリを使用する場合、異なる構造を持つ2つのデータフレーム間で列全体をコピーする方法は一般的な問題です。 2つのデータがあるとします...
 文字列を介してオブジェクトを動的に作成し、Pythonでメソッドを呼び出す方法は?
Apr 01, 2025 pm 11:18 PM
文字列を介してオブジェクトを動的に作成し、Pythonでメソッドを呼び出す方法は?
Apr 01, 2025 pm 11:18 PM
Pythonでは、文字列を介してオブジェクトを動的に作成し、そのメソッドを呼び出す方法は?これは一般的なプログラミング要件です。特に構成または実行する必要がある場合は...
 プロジェクトの基本と問題駆動型の方法で10時間以内にコンピューター初心者プログラミングの基本を教える方法は?
Apr 02, 2025 am 07:18 AM
プロジェクトの基本と問題駆動型の方法で10時間以内にコンピューター初心者プログラミングの基本を教える方法は?
Apr 02, 2025 am 07:18 AM
10時間以内にコンピューター初心者プログラミングの基本を教える方法は?コンピューター初心者にプログラミングの知識を教えるのに10時間しかない場合、何を教えることを選びますか...
 uvicornは、serving_forever()なしでhttpリクエストをどのように継続的に聞いていますか?
Apr 01, 2025 pm 10:51 PM
uvicornは、serving_forever()なしでhttpリクエストをどのように継続的に聞いていますか?
Apr 01, 2025 pm 10:51 PM
UvicornはどのようにしてHTTPリクエストを継続的に聞きますか? Uvicornは、ASGIに基づく軽量のWebサーバーです。そのコア機能の1つは、HTTPリクエストを聞いて続行することです...
 人気のあるPythonライブラリとその用途は何ですか?
Mar 21, 2025 pm 06:46 PM
人気のあるPythonライブラリとその用途は何ですか?
Mar 21, 2025 pm 06:46 PM
この記事では、numpy、pandas、matplotlib、scikit-learn、tensorflow、django、flask、and requestsなどの人気のあるPythonライブラリについて説明し、科学的コンピューティング、データ分析、視覚化、機械学習、Web開発、Hの使用について説明します。
 中間の読書にどこでもfiddlerを使用するときにブラウザによって検出されないようにするにはどうすればよいですか?
Apr 02, 2025 am 07:15 AM
中間の読書にどこでもfiddlerを使用するときにブラウザによって検出されないようにするにはどうすればよいですか?
Apr 02, 2025 am 07:15 AM
fiddlereveryversings for the-middleの測定値を使用するときに検出されないようにする方法





