Pythonでリストの中央値を取得する方法

はじめに

中央値とは、一連の値を上下を均等に分割した値です。リストデータの数が奇数の場合、リストの中央のデータはリストデータの中央値、リストデータの数が偶数の場合、中央の 2 つのデータの算術平均になります。 list はリスト データの中央値です。このタスクでは、自然数を含む空ではない配列 (X) が与えられます。それを上部と下部に分割し、中央値を見つける必要があります。

入力: 配列としての整数 (int) のリスト。

出力: 配列の中央値 (int, float)。

例

get_median([1, 2, 3, 4, 5]) == 3
get_median([3, 1, 2, 5, 3]) == 3
get_median([1, 300, 2, 200, 1]) == 2
get_median([3, 6, 20, 99, 10, 15]) == 12.5

使用方法: 中央値は確率論と統計のアプリケーションで取得されます。偏った分布では大きな価値があります。例: 一連のデータから人々の平均資産を知りたいとします。100 人は月収 100 ドル、10 人は月収 1,000,000 ドルです。平均を計算すると、91,000 ドルになります。これは実際に何が起こっているのかをまったく示さない奇妙な値です。したがって、この場合、中央値はより有用な値とより適切な説明を提供します。

前提条件:<code><strong> </strong>1 < len(data) ≤ 1000 all(0 ≤ x < 10 ** 6 for x in data)

普通方法：

对列表进行排序，针对列表长度是奇数还是偶数的不同情况，计算中位数。

def get_median(data):
   data = sorted(data)
   size = len(data)
   if size % 2 == 0: # 判断列表长度为偶数
    median = (data[size//2]+data[size//2-1])/2
    data[0] = median
   if size % 2 == 1: # 判断列表长度为奇数
    median = data[(size-1)//2]
    data[0] = median
   return data[0]

最佳方法：

这个解决方法非常巧妙，它利用了取反数和为1的特性，通过列表负索引来获得列表中位数。

对 return (data[half] + data[~half]) / 2

1 < len(data) ≤ 1000 all(0 ≤ x < 10 ** for x in data)

通常の方法:

リストを並べ替えて、リストの長さが奇数か偶数かにかかわらず、さまざまなケースの中央値を計算します。

   def get_median(data):
   data.sort()
   half = len(data) // 2
   return (data[half] + data[~half]) / 2

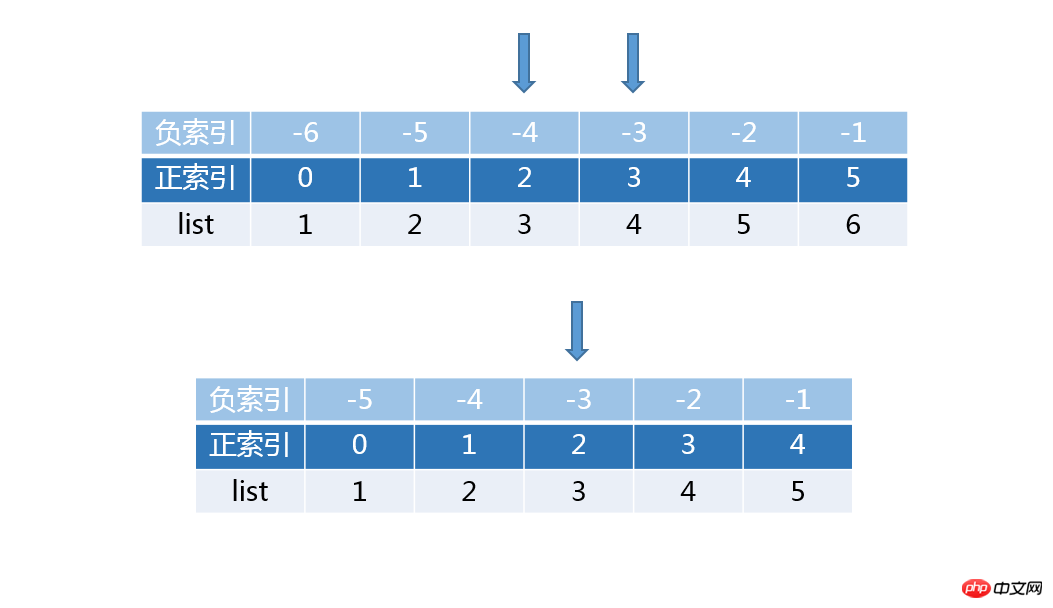
🎜🎜🎜最良の方法: 🎜🎜🎜🎜 この解決策は、逆数の合計が 1 であるという特性を利用して、リストの負のインデックスを通じてリストの中央値を取得します。 🎜🎜 return (data[half] + data[~half]) / 2 の説明: 🎜🎜🎜🎜🎜 ソート後のシーケンス [1,2,3,4,5,6]が取得され、リストの長さは偶数で、中央値はリストの中央の 2 つの要素、3 (インデックス 2) と 4 (インデックス 3) によって決まります。要素 4 の負のインデックスは -3 で、これはインデックス 2 のまさに逆数です。 🎜🎜ソート後、シーケンス [1,2,3,4,5] が得られます。そのリストの長さは奇数であり、中央値はリストの中央の要素 3 によって決まります (インデックスは 2、負のインデックスは-3)。まだコードに準拠しています。 🎜🎜🎜rrreee🎜🎜🎜 Python でリスト (List) の中央値を取得する方法に関するその他の記事については、PHP 中国語 Web サイトに注目してください。 🎜