Pythonで二分探索木を実装する方法-Python チュートリアル-php.cn

BinarySearchTree (バイナリソートツリー) 各ノードのデータ構造は、親ノードポインタ、左の子ポインタ、子ポインタ、そして自身のデータ部分です。なぜなら、子は左右2つしかないからです。これに基づいて、二分木は別の条件も満たします: 各ノードの左の子がノードより大きくない && 各ノードの右の子がノードより大きい

二分探索木

コレクション内のキーと値のペアを取得する 2 つの異なる方法はすでにわかっています。これらのコレクションが ADT (抽象データ型) MAP を実装する方法を思い出してください。 ADT MAP の 2 つの実装、リストベースのバイナリ検索とハッシュテーブルについて説明します。このセクションでは、キーが値を指す別の Map コレクションである二分探索ツリーについて学習します。この場合、ツリー内の要素の実際の位置を考慮する必要はありませんが、知っておく必要があります。バイナリツリーを使用してより多くの情報を効率的に検索する方法。

検索ツリーの操作

この実装を検討する前に、ADT MAP によって提供されるインターフェースを確認してみましょう。このインターフェースは Python の辞書に非常に似ていることがわかります。

Map() は、新しい空の Map コレクションを作成します。
put(key,val) は、新しいキーと値のペアをマップに追加します。キーがすでにマップ内にある場合は、新しい値を使用して古い値が置き換えられます。
get(key) キーを提供するか、Map に保存されているデータを返すか、None を返します。
del del map[key] ステートメントを使用して、マップからキーと値のペアを削除します。
len() は、Map に保存されているキーと値のペアの数を返します
in 指定されたキーが Map 内にある場合、マップステートメントのキーを使用して True を返します。

検索ツリーの実装

左のサブツリーのキー値が親ノードより小さく、右のサブツリーのキー値がすべてより大きい場合の二分探索ツリー親ノードの属性を、私たちがこの種の木をBST検索木と呼びます。前に述べたように、Map を実装するときは、BST メソッドがこれを達成するようにガイドします。図 1 は、二分探索ツリーのこの特性を示しており、値が関連付けられていないキーを示しています。このプロパティはすべての親ノードと子ノードに適用されることに注意してください。左側のサブツリーのすべてのキーはルートノードのキーより小さく、右側のサブツリーのすべてのキーはルートノードのキーより大きくなります。

Pythonで二分探索木を実装する方法

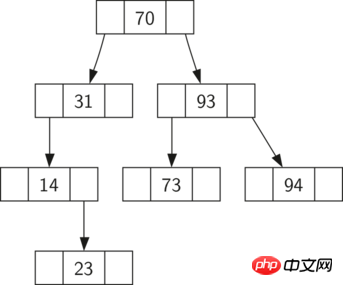
図 1: 単純な二分探索ツリー

二分探索ツリーとは何かを理解したので、二分探索ツリーを構築する方法を見てみましょう。検索ツリーで図 1 に示されているノードに従います。これらのキー値は連続しており、図 1 の検索ツリーに存在するノードは 70、31、93、94、14、23、73 です。 70 はツリーに挿入される最初の値であるため、ルートノードになります。次に、31 は 70 より小さいため、70 の左側のサブツリーになります。次に、93 は 70 より大きいため、70 の右側のサブツリーになります。これでツリーの 2 レベルが埋められたので、次のキー値は 31 または 93 の左または右のサブツリーになります。 94 は 70 および 93 より大きいため、93 の右サブツリーになります。同様に、14 は 70 および 31 より小さいため、31 の左側の部分木になります。 23 も 31 より小さいため、31 の左側のサブツリーでなければなりません。ただし、これは 14 より大きいため、14 の正しいサブツリーになります。

二分探索ツリーを実装するには、リンクリストと式ツリーを実装した方法と同様に、ノードと参照を使用します。空の二分探索ツリーを作成して使用できる必要があるため、2 つのクラスを使用してこれを行います。最初のクラスを BinarySearchTree と呼び、2 番目のクラスを TreeNode と呼びます。 BinarySearchTree クラスには、二分探索ツリーのルートとして TreeNode クラスへの参照があります。ほとんどの場合、外部クラスによって定義された外部メソッドは、ツリー上にノードがあるかどうかを確認するだけで済みます。、BinarySearchTree クラスにプライベートメソッドがパラメータとしてルートを定義することが必要です。この場合、ツリーが空であるか、ツリーのルートを削除したい場合は、特別な操作を使用する必要があります。 BinarySearchTree クラスのconstructor とその他の関数のコードをリスト 1 に示します。

リスト 1

class BinarySearchTree:

  def init(self):
    self.root = None
    self.size = 0

  def length(self):
    return self.size

  def len(self):
    return self.size

  def iter(self):
    return self.root.iter()

ログイン後にコピー

TreeNode クラスは、BinarySearchTree クラスのメソッドの実装プロセスを容易にするための多くの補助関数を提供します。リスト 2 に示すように、ツリーノードの構造はこれらの補助関数によって実装されます。ご覧のとおり、これらのヘルパー関数は、ノードの位置と子のタイプに基づいて、ノードを左または右の子として分割できます。 TreeNode クラスは、各親ノードのプロパティを非常に明確に追跡します。これがなぜ重要であるかは、削除操作の実装について説明するときにわかります。

リスト 2 の TreeNode 実装に関するもう 1 つの興味深い点は、Python のオプションのパラメーターを使用していることです。オプションのパラメーターを使用すると、さまざまな状況でツリーノードを簡単に作成できます。すでに親ノードと子ノードがある場合でも、新しいツリーノードを作成したい場合があります。既存の親ノードと子ノードと同様に、親ノードと子ノードをパラメータとして渡すことができます。場合によっては、キーと値のペアを含むツリーを作成し、親ノードまたは子ノードにパラメーターを渡さないこともあります。この場合、オプションのパラメータのデフォルト値を使用します。

リスト 2

class TreeNode:
  def init(self,key,val,left=None,right=None,
                    parent=None):
    self.key = key
    self.payload = val
    self.leftChild = left
    self.rightChild = right
    self.parent = parent

  def hasLeftChild(self):
    return self.leftChild

  def hasRightChild(self):
    return self.rightChild

  def isLeftChild(self):
    return self.parent and self.parent.leftChild == self

  def isRightChild(self):
    return self.parent and self.parent.rightChild == self

  def isRoot(self):
    return not self.parent

  def isLeaf(self):
    return not (self.rightChild or self.leftChild)

  def hasAnyChildren(self):
    return self.rightChild or self.leftChild

  def hasBothChildren(self):
    return self.rightChild and self.leftChild

  def replaceNodeData(self,key,value,lc,rc):
    self.key = key
    self.payload = value
    self.leftChild = lc
    self.rightChild = rc
    if self.hasLeftChild():
      self.leftChild.parent = self
    if self.hasRightChild():
      self.rightChild.parent = self

ログイン後にコピー

BinarySearchTree クラスと TreeNode クラスを用意したので、二分探索ツリーを構築できる put メソッドを作成します。 putメソッドはBinarySearchTreeクラスのメソッドです。このメソッドは、ツリーがすでにルート化されているかどうかを確認します。そうでない場合は、新しいツリーノードを作成し、それをツリーのルートとして設定します。すでにルートノードがある場合は、それを自分で呼び出し、再帰を実行し、補助関数 _put を使用して次のアルゴリズムに従ってツリーを検索します:

ツリーのルートノードから開始し、新しいキー値を比較します。バイナリツリーを検索して現在のキー値と比較します。新しいキー値が現在のノードより小さい場合は、左側のサブツリーが検索されます。新しいキーが現在のノードより大きい場合は、右側のサブツリーが検索されます。

左 (または右) のサブツリーが検索できない場合、ツリー内の位置が新しいノードが設定される場所になります。
ツリーにノードを追加するには、新しい TreeNode オブジェクトを作成し、このオブジェクトをこの時点より前のノードに挿入します。

リスト 3 は、ツリーに新しいノードを挿入する Python コードを示しています。 _put 関数は、上記の手順に従って再帰アルゴリズムを作成する必要があります。新しいサブツリーが挿入されると、現在のノード (CurrentNode) が親ノードとして新しいツリーに渡されることに注意してください。

挿入を実行するときの重要な問題は、重複したキー値を正しく処理できないことです。ツリーはキー値のレプリケーションを実装しており、元のノードと同じキー値を持つ新しいノードが右のサブツリーに作成されます。この結果、検索中に新しいノードが検出されなくなります。重複したキー値の挿入を処理するためのより良い方法を使用します。古い値は、新しいキーに関連付けられた値で置き換えられます。このバグの修正は演習として残しておきます。

リスト 3

def put(self,key,val):
  if self.root:
    self._put(key,val,self.root)
  else:
    self.root = TreeNode(key,val)
  self.size = self.size + 1

def _put(self,key,val,currentNode):
  if key < currentNode.key:
    if currentNode.hasLeftChild():
        self._put(key,val,currentNode.leftChild)
    else:
        currentNode.leftChild = TreeNode(key,val,parent=currentNode)
  else:
    if currentNode.hasRightChild():
        self._put(key,val,currentNode.rightChild)
    else:
        currentNode.rightChild = TreeNode(key,val,parent=currentNode)

ログイン後にコピー

put メソッドを実装すると、setitem メソッドのオーバーロード [] を operator として使用して簡単に put メソッドを呼び出すことができます (リスト 4 を参照)。これにより、myZipTree['Plymouth'] = 55446 のような Python ステートメントを作成できるようになり、Python 辞書のように見えます。

リスト 4

def setitem(self,k,v):
  self.put(k,v)

ログイン後にコピー

図 2 は、二分探索ツリーに新しいノードを挿入するプロセスを示しています。灰色のノードは、挿入プロセス中にたどられるツリーノードの順序を示します。

Pythonで二分探索木を実装する方法

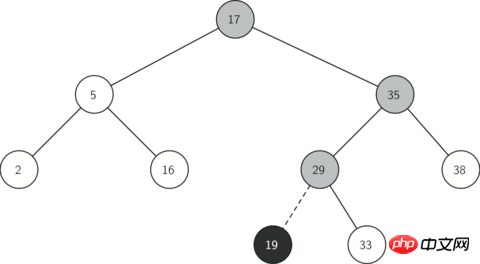
図 2: キー値 = 19 のノードの挿入

ツリーが構築されたら、次のタスクは、指定されたキー値の取得を実装することです。 get メソッドは、不一致のリーフノードが見つかるか、一致するキー値が見つかるまでツリーを再帰的に検索するだけなので、put メソッドよりも簡単です。一致するキー値が見つかると、ノード内の値が返されます。

リスト 5 は、get、_get、getitem のコードを示しています。 _get メソッドで検索されるコードには、put メソッドと同じ左または右のサブツリーを選択するロジックが含まれています。 _get メソッドは TreeNode の get の値を返します。_get は、TreeNode のデータを使用する必要がある BinarySearchTree の他のメソッドにパラメータを提供する柔軟かつ効果的な方法として使用できることに注意してください。

getitem メソッドを実装することで、実際には Z = myziptree['fargo'] などの二分探索ツリーを操作しているだけであるにもかかわらず、辞書にアクセスしているように見える Python ステートメントを作成できます。ご覧のとおり、getitem メソッドは get を呼び出しています。

リスト 5

def get(self,key):
  if self.root:
    res = self._get(key,self.root)
    if res:
        return res.payload
    else:
        return None
  else:
    return None

def _get(self,key,currentNode):
  if not currentNode:
    return None
  elif currentNode.key == key:
    return currentNode
  elif key < currentNode.key:
    return self._get(key,currentNode.leftChild)
  else:
    return self._get(key,currentNode.rightChild)

def getitem(self,key):
  return self.get(key)

ログイン後にコピー

使用get，我们可以通过写一个BinarySearchTree的contains方法来实现操作，contains方法简单地调用了get方法，如果它有返回值就返回True，如果它是None就返回False。如Listing 6 所示。

Listing 6

def contains(self,key):
  if self._get(key,self.root):
    return True
  else:
    return False

ログイン後にコピー

回顾一下contains重载的操作符，这允许我们写这样的语句：

if &#39;Northfield&#39; in myZipTree:
  print("oom ya ya")

ログイン後にコピー

以上がPythonで二分探索木を実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。