Pythonでの最小二乗法の使い方を詳しく解説

「実装」ではなく「使用」と言っている理由は、Python の関連クラス ライブラリが特定のアルゴリズムの実装にすでに役立っており、それらの使い方を学ぶだけで十分だからです。テクノロジーが徐々に習得され蓄積されると、クラス ライブラリ内のアルゴリズムが自分たちのニーズを満たせなくなった場合、独自の方法でさまざまなアルゴリズムを実装してみることもできます。

本題に戻りますが、「最小二乗法」とは何ですか？

定義: 最小二乗法 (最小二乗法とも呼ばれます) は、誤差の二乗和を最小化することによって、データに最もよく一致する関数を見つける数学的最適化手法です。

機能: 最小二乗法を使用すると、未知のデータを簡単に取得し、取得したデータと実際のデータの間の二乗誤差の合計を最小限に抑えることができます。

原則: 「残差の二乗和の最小値」で直線の位置を決定します (数学的統計において、残差とは実際の観測値と推定値の差を指します)

基本的な考え方: 線形の場合1 変数の回帰モデルで、平面上のこれらの n 点に対して、全体の n 組の観測値 (X1, Y1), (X2, Y2), ..., (Xn, Yn) が得られるとします。無数の曲線を使用してそれらをフィットさせることができます。線形回帰では、サンプル回帰関数がこの一連の値にできるだけ適合する必要があります。つまり、この直線はサンプル データのできるだけ中心にある必要があります。したがって、最良のフィッティング曲線を選択するための基準は、合計のフィッティング誤差 (つまり、合計の残差誤差) を最小化することとして決定できます。

実装コードは次のとおりであり、コードは詳細にコメントされています:

##最小二乘法
import numpy as np   ##科学计算库 
import scipy as sp   ##在numpy基础上实现的部分算法库
import matplotlib.pyplot as plt  ##绘图库
from scipy.optimize import leastsq  ##引入最小二乘法算法

'''
     设置样本数据，真实数据需要在这里处理
'''
##样本数据(Xi,Yi)，需要转换成数组(列表)形式
Xi=np.array([6.19,2.51,7.29,7.01,5.7,2.66,3.98,2.5,9.1,4.2])
Yi=np.array([5.25,2.83,6.41,6.71,5.1,4.23,5.05,1.98,10.5,6.3])

'''
    设定拟合函数和偏差函数
    函数的形状确定过程：
    1.先画样本图像
    2.根据样本图像大致形状确定函数形式(直线、抛物线、正弦余弦等)
'''

##需要拟合的函数func :指定函数的形状
def func(p,x):
    k,b=p
    return k*x+b

##偏差函数：x,y都是列表:这里的x,y更上面的Xi,Yi中是一一对应的
def error(p,x,y):
    return func(p,x)-y

'''
    主要部分：附带部分说明
    1.leastsq函数的返回值tuple，第一个元素是求解结果，第二个是求解的代价值(个人理解)
    2.官网的原话（第二个值）：Value of the cost function at the solution
    3.实例：Para=>(array([ 0.61349535,  1.79409255]), 3)
    4.返回值元组中第一个值的数量跟需要求解的参数的数量一致
'''

#k,b的初始值，可以任意设定,经过几次试验，发现p0的值会影响cost的值：Para[1]
p0=[1,20]

#把error函数中除了p0以外的参数打包到args中(使用要求)
Para=leastsq(error,p0,args=(Xi,Yi))

#读取结果
k,b=Para[0]
print("k=",k,"b=",b)
print("cost："+str(Para[1]))
print("求解的拟合直线为:")
print("y="+str(round(k,2))+"x+"+str(round(b,2)))

'''
   绘图，看拟合效果.
   matplotlib默认不支持中文，label设置中文的话需要另行设置
   如果报错，改成英文就可以
'''

#画样本点
plt.figure(figsize=(8,6)) ##指定图像比例： 8：6
plt.scatter(Xi,Yi,color="green",label="样本数据",linewidth=2) 

#画拟合直线
x=np.linspace(0,12,100) ##在0-15直接画100个连续点
y=k*x+b ##函数式
plt.plot(x,y,color="red",label="拟合直线",linewidth=2) 
plt.legend() #绘制图例
plt.show()

結果は次のとおりです:

出力結果:

k= 0.900458420439 b= 0.831055638877
コスト: 1
に適合した直線解くべきことは:
y =0.9x+0.83

描画結果:

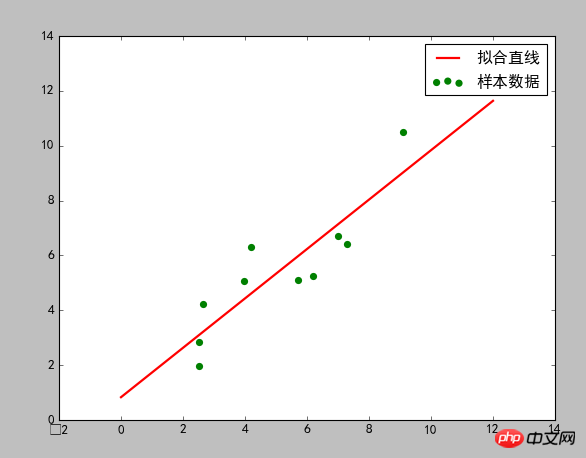
以上がPythonでの最小二乗法の使い方を詳しく解説の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。