
この記事では、C#、バブル ソート、クイック ソートなどの 7 つの古典的なソート アルゴリズムのシリーズの最初の部分を主に詳細に紹介します。興味のある友人は参照してください。
今日は始まりなので、アルゴリズムについて話したいと思います。プログラム開発において、アルゴリズムは鋭い剣のようなものです。
現実の並べ替え問題の場合、アルゴリズムには成功に役立つ 7 つの鋭い剣があります。
まず、選別には4種類あります:
交換選別: バブル選別とクイック選別を含む。
選択ソート: 直接選択ソートとヒープソートを含みます。
挿入ソート:直接挿入ソート、ヒルソートを含む。
並べ替えを結合: 並べ替えを結合します。
それでは、今日は交換ソートについて話します。C# クラス ライブラリによって提供されるソートがクイック ソートであることは誰もが知っています。今日は、それをさらに面白くするために、
によって提供されるクイック ソートと競合するアルゴリズムを設計します。クラスライブラリ。相手をKOするために戦いましょう。
バブル選別:
まず、私たち自身で「バブル選別」を設計します。この種の選別の非常に現実的な例は次のとおりです:
一掴みの砂をつかんで水の中に入れると、砂はすぐに消えます。砂上の塵は慣性により一時的に水底に沈みますが、すぐに泡のように浮上し、最後に真実が明らかになります。
湧き出る感想に関しては、そんな公式論は語りませんし、ただ写真を見て思っているだけです。
それでは、上の写真を見てみましょう。
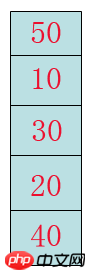
泡立つ効果を実現するには、一連の数字を立てて、それらを観察する必要があります。考えてみてください。どうやって泡を立てるのでしょうか?重いものは底に沈み、軽いものは浮くということをどのように理解すればよいでしょうか?
ステップ 1: 40 と 20 を比較し、40 がボスであり、交換する必要がないことがわかります。
ステップ 2: 次に、一歩前進します。つまり、20 と 30 を比較します。30 がボスであることがわかった場合は、交換する必要があります。
ステップ 3: 交換した 20 と 10 を比較し、あなたがボスで交換する必要がないことがわかります。
ステップ 4: 10 を 50 と交換し、50 がボスであることを確認し、交換します。
最後に、走査の後、配列内の最小の数値を送信しました。これで、ゴールに向かって新たな一歩を踏み出すことができました。
今、誰もが何を考えているかを知っているので、私たちはあなたが死ぬか私が生きるか、クイックキューで競争することを強く要求します。
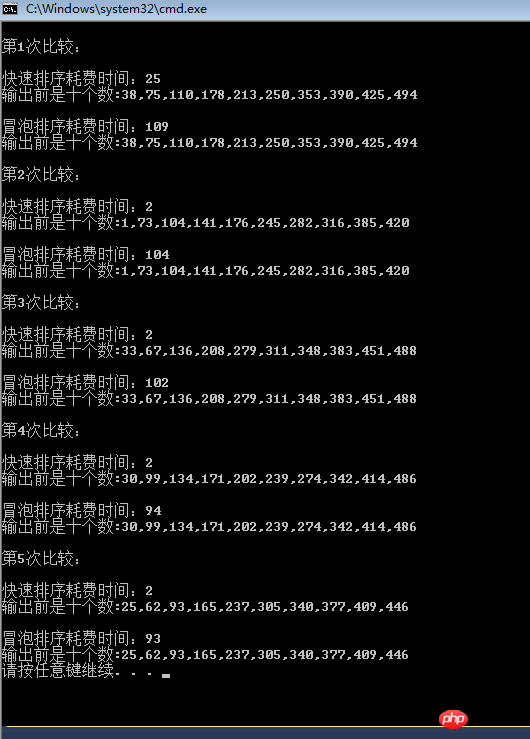
うわー、この2つの健康診断のレポートを見て、バブリングの効率が低いと言われても不思議ではありませんでした。本当に低いことが分かりました。
クイックソート:
バブルをKOできるので、すぐに興味が湧きました。クイックソートは非常に速いので、注意深く研究する必要があります。
まず、上の写真を撮ってみましょう:

この写真から、
左ポインター、右ポインター、ベース参照番号がわかります。
実際、アイデアは非常に単純で、トラバーサルの最初のパスで配列の切断点を見つけることです (左右のポインターを一致させます)。
ステップ 1: まず、配列の左端の番号 (20) を基本参照オブジェクトとして取得します。 step 2:(ベース)よりも小さい数字が見つかるまで、配列の右の位置から前方に検索します。 、10、60。组 ステップ 3: 配列の左の位置から振り返って、常に (Base) より大きな数値を見つけたら、その数値を右の位置に与えます (つまり、配列が 40 から 10 になるまで)。 : 10、40、50、40、60、
左右のポインターは前後で 40 です。
第四步:重复「第二、第三」步ステップ、左と右の指针まで重ね、
最後に(ベース)40の位置に進入、
この時点の数構成は: 10、20、50、 40、60、これで仕分けは完了です。
ステップ 5: この時点で、20 は配列の内部に忍び込みました。20 の左側の数値はすべて 20 より小さく、20 の右側の数値はすべて 20 より大きくなります。
以20为切入点对左右两边数按照"第一,第二,第三,第四"步骤进行,最终快排大功告成。
同样,我们把自己设计的快排跟类库提供的快拍比较一下。
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading;
using System.Diagnostics;
namespace QuickSort
{
public class Program
{
static void Main(string[] args)
{
//5次比较
for (int i = 1; i <= 5; i++)
{
List<int> list = new List<int>();
//插入200个随机数到数组中
for (int j = 0; j < 200; j++)
{
Thread.Sleep(1);
list.Add(new Random((int)DateTime.Now.Ticks).Next(0, 10000));
}
Console.WriteLine("\n第" + i + "次比较:");
Stopwatch watch = new Stopwatch();
watch.Start();
var result = list.OrderBy(single => single).ToList();
watch.Stop();
Console.WriteLine("\n系统定义的快速排序耗费时间:" + watch.ElapsedMilliseconds);
Console.WriteLine("输出前是十个数:" + string.Join(",", result.Take(10).ToList()));
watch.Start();
new QuickSortClass().QuickSort(list, 0, list.Count - 1);
watch.Stop();
Console.WriteLine("\n俺自己写的快速排序耗费时间:" + watch.ElapsedMilliseconds);
Console.WriteLine("输出前是十个数:" + string.Join(",", list.Take(10).ToList()));
}
}
}
public class QuickSortClass
{
///<summary>
/// 分割函数
///</summary>
///<param name="list">待排序的数组</param>
///<param name="left">数组的左下标</param>
///<param name="right"></param>
///<returns></returns>
public int pision(List<int> list, int left, int right)
{
//首先挑选一个基准元素
int baseNum = list[left];
while (left < right)
{
//从数组的右端开始向前找,一直找到比base小的数字为止(包括base同等数)
while (left < right && list[right] >= baseNum)
right = right - 1;
//最终找到了比baseNum小的元素,要做的事情就是此元素放到base的位置
list[left] = list[right];
//从数组的左端开始向后找,一直找到比base大的数字为止(包括base同等数)
while (left < right && list[left] <= baseNum)
left = left + 1;
//最终找到了比baseNum大的元素,要做的事情就是将此元素放到最后的位置
list[right] = list[left];
}
//最后就是把baseNum放到该left的位置
list[left] = baseNum;
//最终,我们发现left位置的左侧数值部分比left小,left位置右侧数值比left大
//至此,我们完成了第一篇排序
return left;
}
public void QuickSort(List<int> list, int left, int right)
{
//左下标一定小于右下标,否则就超越了
if (left < right)
{
//对数组进行分割,取出下次分割的基准标号
int i = pision(list, left, right);
//对“基准标号“左侧的一组数值进行递归的切割,以至于将这些数值完整的排序
QuickSort(list, left, i - 1);
//对“基准标号“右侧的一组数值进行递归的切割,以至于将这些数值完整的排序
QuickSort(list, i + 1, right);
}
}
}
}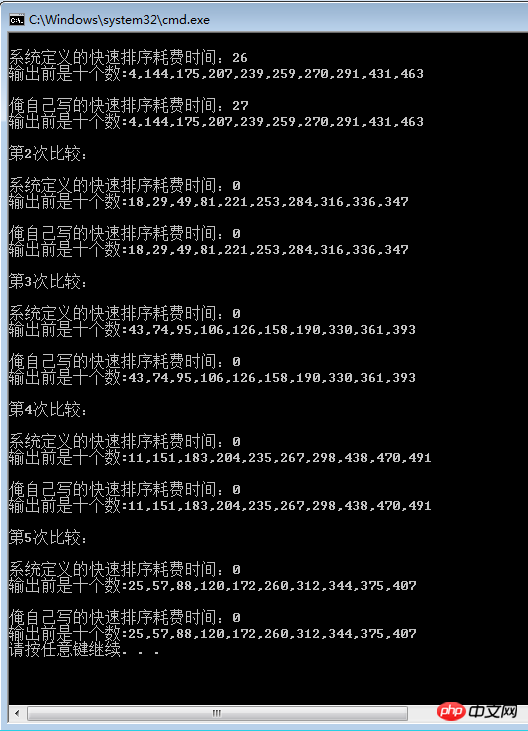
不错,快排就是快,难怪内库非要用他来作为排序的标准。
嗯,最后要分享下:
冒泡的时间复杂度为:0(n) - 0(n^2)
快排的时间复杂度为:
平均复杂度:N(logN)
最坏复杂度: 0(n^2)
以上がC#クラシックソートアルゴリズムのグラフィックコードを詳しく解説(前編)の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。