この記事では主に C# について詳しく紹介します 7 つの古典的なソート アルゴリズムの第 2 部、直接挿入ソート、ヒル ソート、マージ ソートについては、一定の参考値がありますので、興味のある方は参考にしてください。最後の 3 つのソート、直接挿入ソート、ヒル ソート、マージ ソートについて説明します。
直接挿入ソート:
この種のソートは実際には非常に簡単に理解できます。非常に現実的な例は、カードのランダムなハンドをキャッチしたときに、そのサイズに応じてポーカー カードを分類する必要があります。 30 秒後、ポーカー カードが並べ替えられました。3 が 4 枚、5 枚が並べられました。そのときの並べ替え方法を思い出してください。
一番左のカードは 3、2 番目のカードは 5、3 番目のカードは再び 3、すぐに最初のカードの後ろに挿入、4 番目のカードは再び 3、とても満足です、すぐに 2 番目のカードに挿入します。裏に行き、5枚目がまた3で大砲が生まれました(笑)。 どうですか? アルゴリズムは生活のあらゆるところにあり、すでに私たちの生活と血液に組み込まれています。 以下は上の図の説明です:この図を理解していただけたでしょうか。挿入ソートでは、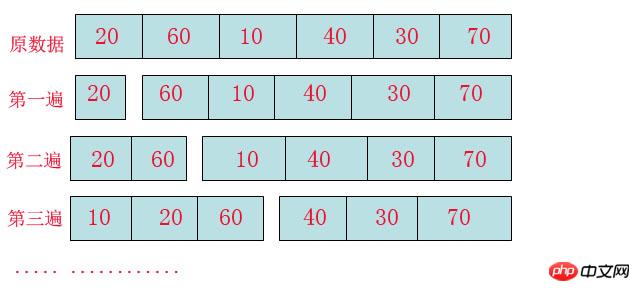 配列
配列
2 番目のパスでは、数値 60 が「順序なし配列ブロック」から抽出され、「順序付き配列ブロック」(つまり 20、60) に順序どおりに配置されます。
3 番目のパスでも同じことが当てはまりますが、違いは、10 が順序付けされた配列の値より小さいことが判明したため、20 と 60 の位置が戻されて、10 を挿入するための位置が解放されることです。 その後、すべての挿入はこのルールに従って完了できます。using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace InsertSort
{
public class Program
{
static void Main(string[] args)
{
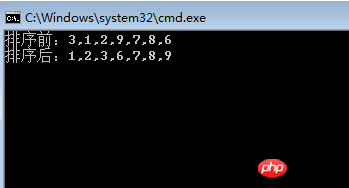
List<int> list = new List<int>() { 3, 1, 2, 9, 7, 8, 6 };
Console.WriteLine("排序前:" + string.Join(",", list));
InsertSort(list);
Console.WriteLine("排序后:" + string.Join(",", list));
}
static void InsertSort(List<int> list)
{
//无须序列
for (int i = 1; i < list.Count; i++)
{
var temp = list[i];
int j;
//有序序列
for (j = i - 1; j >= 0 && temp < list[j]; j--)
{
list[j + 1] = list[j];
}
list[j + 1] = temp;
}
}
}
} ヒルソート:
ヒルソート:
「挿入ソート」を観察してください: 実際、欠点があることを見つけるのは難しくありません:
データが「5, 4, 3」の場合, 2, 1
」の場合、「順序なしブロック」にあるレコードを「順序付きブロック」に挿入すると潰れることが予想され、挿入するたびに位置が移動します。このときの効率は挿入ソートの想像ができます。Shell はこの弱点に基づいてアルゴリズムを改善し、「縮小増分ソート方法
」と呼ばれるアイデアを組み込みました。これは実際には非常に単純ですが、注意すべき点は次のとおりです:増分はランダムに取得されません。フォローする。
まず、増分を選択する方法を明確にする必要があります。まで: d = 1; 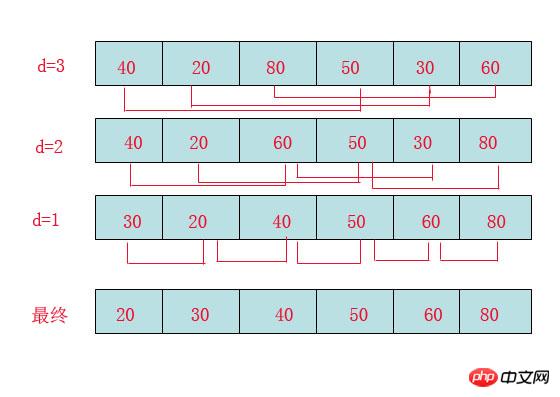
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading;
using System.Diagnostics;
namespace ShellSort
{
public class Program
{
static void Main(string[] args)
{
//5次比较
for (int i = 1; i <= 5; i++)
{
List<int> list = new List<int>();
//插入1w个随机数到数组中
for (int j = 0; j < 10000; j++)
{
Thread.Sleep(1);
list.Add(new Random((int)DateTime.Now.Ticks).Next(10000, 1000000));
}
List<int> list2 = new List<int>();
list2.AddRange(list);
Console.WriteLine("\n第" + i + "次比较:");
Stopwatch watch = new Stopwatch();
watch.Start();
InsertSort(list);
watch.Stop();
Console.WriteLine("\n插入排序耗费的时间:" + watch.ElapsedMilliseconds);
Console.WriteLine("输出前十个数:" + string.Join(",", list.Take(10).ToList()));
watch.Restart();
ShellSort(list2);
watch.Stop();
Console.WriteLine("\n希尔排序耗费的时间:" + watch.ElapsedMilliseconds);
Console.WriteLine("输出前十个数:" + string.Join(",", list2.Take(10).ToList()));
}
}
///<summary>
/// 希尔排序
///</summary>
///<param name="list"></param>
static void ShellSort(List<int> list)
{
//取增量
int step = list.Count / 2;
while (step >= 1)
{
//无须序列
for (int i = step; i < list.Count; i++)
{
var temp = list[i];
int j;
//有序序列
for (j = i - step; j >= 0 && temp < list[j]; j = j - step)
{
list[j + step] = list[j];
}
list[j + step] = temp;
}
step = step / 2;
}
}
///<summary>
/// 插入排序
///</summary>
///<param name="list"></param>
static void InsertSort(List<int> list)
{
//无须序列
for (int i = 1; i < list.Count; i++)
{
var temp = list[i];
int j;
//有序序列
for (j = i - 1; j >= 0 && temp < list[j]; j--)
{
list[j + 1] = list[j];
}
list[j + 1] = temp;
}
}
}
}スクリーンショットは次のとおりです:
wレベルのソートでは、差が70以上であることがわかります。回。マージソート:
個人的には、分かりやすいソートは基本的にO(n^2)、理解しにくいソートは基本的にN(LogN)なので、マージソートも難しくなります。わかります、特にコードの書き方に関しては
、それを理解するのに丸一日かかりました、ふふ。
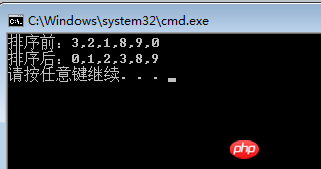
まず画像を見てください: 
マージソートでは行うべきことが 2 つあります: 第一: “分”, 就是将数组尽可能的分,一直分到原子级别。 第二: “并”,将原子级别的数两两合并排序,最后产生结果。 代码: 结果图: ps: 插入排序的时间复杂度为:O(N^2) 希尔排序的时间复杂度为:平均为:O(N^3/2) 最坏:O(N^2) 归并排序时间复杂度为: O(NlogN) 空间复杂度为: O(N) 以上がC#クラシックソートアルゴリズムのグラフィックコードを詳しく解説(後編)の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace MergeSort
{
class Program
{
static void Main(string[] args)
{
int[] array = { 3, 2, 1, 8, 9, 0 };
MergeSort(array, new int[array.Length], 0, array.Length - 1);
Console.WriteLine(string.Join(",", array));
}
///<summary>
/// 数组的划分
///</summary>
///<param name="array">待排序数组</param>
///<param name="temparray">临时存放数组</param>
///<param name="left">序列段的开始位置,</param>
///<param name="right">序列段的结束位置</param>
static void MergeSort(int[] array, int[] temparray, int left, int right)
{
if (left < right)
{
//取分割位置
int middle = (left + right) / 2;
//递归划分数组左序列
MergeSort(array, temparray, left, middle);
//递归划分数组右序列
MergeSort(array, temparray, middle + 1, right);
//数组合并操作
Merge(array, temparray, left, middle + 1, right);
}
}
///<summary>
/// 数组的两两合并操作
///</summary>
///<param name="array">待排序数组</param>
///<param name="temparray">临时数组</param>
///<param name="left">第一个区间段开始位置</param>
///<param name="middle">第二个区间的开始位置</param>
///<param name="right">第二个区间段结束位置</param>
static void Merge(int[] array, int[] temparray, int left, int middle, int right)
{
//左指针尾
int leftEnd = middle - 1;
//右指针头
int rightStart = middle;
//临时数组的下标
int tempIndex = left;
//数组合并后的length长度
int tempLength = right - left + 1;
//先循环两个区间段都没有结束的情况
while ((left <= leftEnd) && (rightStart <= right))
{
//如果发现有序列大,则将此数放入临时数组
if (array[left] < array[rightStart])
temparray[tempIndex++] = array[left++];
else
temparray[tempIndex++] = array[rightStart++];
}
//判断左序列是否结束
while (left <= leftEnd)
temparray[tempIndex++] = array[left++];
//判断右序列是否结束
while (rightStart <= right)
temparray[tempIndex++] = array[rightStart++];
//交换数据
for (int i = 0; i < tempLength; i++)
{
array[right] = temparray[right];
right--;
}
}
}
}