Pythonの一般的なソートコードの詳細な説明-Python チュートリアル-php.cn

この記事は主に Python アルゴリズムの基本的なチュートリアルを詳しく紹介していますので、興味のある方は参考にしてください。無駄だったので Niuke.com に行って 2 日かけて質問してみました... このブログでは、いくつかの簡単な/一般的な並べ替えアルゴリズムを紹介します。

時間計算量

(1) 時間頻度

アルゴリズムの実行にかかる時間は理論的に計算できません

。それを知るには、コンピューター上でテストを実行する必要があります。しかし、コンピューター上ですべてのアルゴリズムをテストすることは不可能であり、その必要はありません。必要なのは、どのアルゴリズムに時間がかかり、どのアルゴリズムに時間がかからないかだけです。また、アルゴリズムにかかる時間は、アルゴリズム内のステートメントの実行数に比例し、より多くのステートメントを含むアルゴリズムが実行されると、より多くの時間がかかります。アルゴリズムにおけるステートメントの実行数は、ステートメント頻度または時間頻度と呼ばれます。それをT(n)と表します。 (2) 時間計算量先ほどの時間周波数において、

n は問題のスケールと呼ばれます。n が変化し続けると、時間周波数 T(n) も変化し続けます

。しかし、場合によっては、変化したときにどのようなパターンが示されるかを知りたいことがあります。この目的のために、時間計算量の概念を導入します。一般に、アルゴリズムの基本演算の繰り返し回数は、T(n) で表される問題サイズ n の関数です。ある補助関数 f(n) がある場合、は n のときに次のようになります。 (n)/f(n) の限界値が 0 に等しくない定数である場合、f(n) は T(n) と同じ桁の大きさの関数であると言われます。 T(n)=O(f(n)) で表される O(f(n)) は、アルゴリズムの漸近時間計算量、または略して時間計算量と呼ばれます。

指数関数的時間は、問題を解くのに必要な計算時間 m(n) を指し、入力データのサイズに応じて指数関数的に増加します (つまり、入力データの量が線形に増加し、時間が増加します)。必要な時間は指数関数的に増加します)

for (i=1; i<=n; i++)
 x++;
for (i=1; i<=n; i++)
 for (j=1; j<=n; j++)
 x++;

ログイン後にコピー

最初の for ループの時間計算量は Ο(n)、2 番目の for ループの時間計算量は Ο(n2)、その後、アルゴリズム全体の時間計算量は Ο (n+n2)=Ο(n2)。

定数時間アルゴリズムの上限が入力サイズに依存しない場合、そのアルゴリズムは定数時間を持ち、時間として記録されると言われます。例としては、配列内の 1 つの要素にアクセスする場合です。これは、アクセスに必要な命令が 1 つだけであるためです。ただし、順序なし配列で最小の要素を見つけることはできません。これは、最小値を見つけるためにすべての要素をループする必要があるためです。これは線形時間操作、つまり時間です。しかし、要素の数が事前にわかっていて、その数が一定であると仮定する場合、演算は定数時間であるとも言えます。

対数時間アルゴリズムの

T(n) =O(logn)の場合、

は対数時間を持つと言われます対数時間の一般的なアルゴリズムには、二分木と二分探索の関連演算が含まれます。

対数時間アルゴリズムは、入力が追加されるたびに必要な追加の計算時間が小さくなるため、非常に効率的です。文字列を再帰的に半分に切り、出力するのは、このカテゴリの関数の簡単な例です。各出力の前に文字列を半分にカットするため、O(log n) 時間がかかります。これは、出力の数を増やしたい場合は、文字列の長さを 2 倍にする必要があることを意味します。

線形時間

アルゴリズムの時間計算量が O(n) の場合、アルゴリズムは線形時間

、または O(n) 時間を有すると言われます。非公式には、これは、入力が十分に大きい場合、実行時間は入力のサイズに比例して増加することを意味します。たとえば、リストのすべての要素の合計を計算するプログラムには、リストの長さに比例して時間がかかります。

1. バブルアルゴリズム

基本的な考え方:

並べ替える一連の数値において、現在並べ替えられていない範囲内のすべての数値について、隣接する 2 つの数値を上から下に並べ替えます。数値は次のとおりです。順番に比較および調整され、大きい数値が沈み、小さい数値が上昇します。つまり、2 つの隣接する数値を比較し、それらの順序が順序要件と逆であることが判明した場合は常に、それらの数値が交換されます。

バブルソートの例:

アルゴリズム実装:

def bubble(array):
 for i in range(len(array)-1):
 for j in range(len(array)-1-i):
 if array[j] > array[j+1]: # 如果前一个大于后一个，则交换
 temp = array[j]
 array[j] = array[j+1]
 array[j+1] = temp


if __name__ == "__main__":
 array = [265, 494, 302, 160, 370, 219, 247, 287,
 354, 405, 469, 82, 345, 319, 83, 258, 497, 423, 291, 304]
 print("------->排序前<-------")
 print(array)
 bubble(array)
 print("------->排序后<-------")
 print(array)

ログイン後にコピー

出力:

------>ソート前<------

[265 、494、302、160、370、219、247、287、354、405、469、82、345、319、83、258、497、423、291、304]

------>ソート後< ;----------

[82, 83, 160, 219, 247, 258, 265, 287, 291, 302, 304, 319, 345, 354, 370, 405, 423, 469 , 494, 497]

説明:

以随机产生的五个数为例:　li=[354,405,469,82,345]
冒泡排序是怎么实现的?
首先先来个大循环，每次循环找出最大的数，放在列表的最后面。在上面的例子中，第一次找出最大数469，将469放在最后一个，此时我们知道
列表最后一个肯定是最大的，故还需要再比较前面4个数，找出4个数中最大的数405，放在列表倒数第二个......

5个数进行排序，需要多少次的大循环??　当然是4次啦!同理，若有n个数，需n-1次大循环。

现在你会问我: 第一次找出最大数469，将469放在最后一个??怎么实现的??
嗯，（在大循环里）用一个小循环进行两数比较，首先354与405比较，若前者较大，需要交换数；反之不用交换。
当469与82比较时，需交换，故列表倒数第二个为469；469与345比较，需交换，此时最大数469位于列表最后一个啦!

难点来了，小循环需要多少次??

进行两数比较，从列表头比较至列表尾，此时需len(array)-1次!! 但是，嗯，举个例子吧: 当大循环i为3时，说明此时列表的最后3个数已经排好序了，不必进行两数比较，故小循环需len(array)-1-3.　即len(array)-1-i

冒泡排序复杂度:

时间复杂度: 最好情况O(n), 最坏情况O(n^2), 平均情况O(n^2)

空间复杂度: O(1)

稳定性: 稳定

简单选择排序的示例：

二、选择排序

The selection sort works as follows: you look through the entire array for the smallest element, once you find it you swap it (the smallest element) with the first element of the array. Then you look for the smallest element in the remaining array (an array without the first element) and swap it with the second element. Then you look for the smallest element in the remaining array (an array without first and second elements) and swap it with the third element, and so on. Here is an example

基本思想：

在要排序的一组数中，选出最小（或者最大）的一个数与第1个位置的数交换；然后在剩下的数当中再找最小（或者最大）的与第2个位置的数交换，依次类推，直到第n-1个元素（倒数第二个数）和第n个元素（最后一个数）比较为止。

简单选择排序的示例：

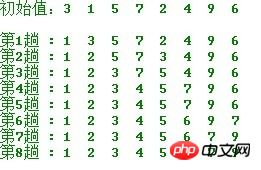
算法实现:

def select_sort(array):
 for i in range(len(array)-1): # 找出最小的数放与array[i]交换
 for j in range(i+1, len(array)):
 if array[i] > array[j]:
 temp = array[i]
 array[i] = array[j]
 array[j] = temp


if __name__ == "__main__":
 array = [265, 494, 302, 160, 370, 219, 247, 287,
 354, 405, 469, 82, 345, 319, 83, 258, 497, 423, 291, 304]
 print(array)
 select_sort(array)
 print(array)

ログイン後にコピー

选择排序复杂度:

时间复杂度: 最好情况O(n^2), 最坏情况O(n^2), 平均情况O(n^2)

空间复杂度: O(1)

稳定性: 不稳定

举个例子：序列5 8 5 2 9，我们知道第一趟选择第1个元素5会与2进行交换，那么原序列中两个5的相对先后顺序也就被破坏了。

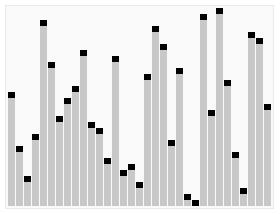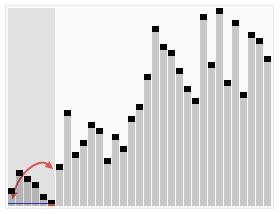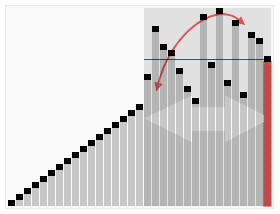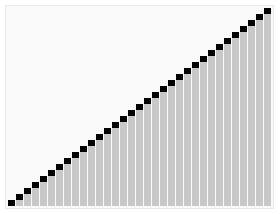
排序效果：

三、直接插入排序

插入排序(Insertion Sort)的基本思想是：将列表分为2部分，左边为排序好的部分，右边为未排序的部分，循环整个列表，每次将一个待排序的记录，按其关键字大小插入到前面已经排好序的子序列中的适当位置，直到全部记录插入完成为止。

插入排序非常类似于整扑克牌。

在开始摸牌时，左手是空的，牌面朝下放在桌上。接着，一次从桌上摸起一张牌，并将它插入到左手一把牌中的正确位置上。为了找到这张牌的正确位置，要将它与手中已有的牌从右到左地进行比较。无论什么时候，左手中的牌都是排好序的。

也许你没有意识到，但其实你的思考过程是这样的：现在抓到一张7，把它和手里的牌从右到左依次比较，7比10小，应该再往左插，7比5大，好，就插这里。为什么比较了10和5就可以确定7的位置？为什么不用再比较左边的4和2呢？因为这里有一个重要的前提：手里的牌已经是排好序的。现在我插了7之后，手里的牌仍然是排好序的，下次再抓到的牌还可以用这个方法插入。编程对一个数组进行插入排序也是同样道理，但和插入扑克牌有一点不同，不可能在两个相邻的存储单元之间再插入一个单元，因此要将插入点之后的数据依次往后移动一个单元。

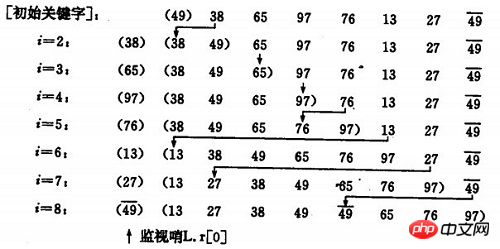
设监视哨是我大一在书上有看过，大家忽视上图的监视哨。

算法实现:

import time


def insertion_sort(array):
 for i in range(1, len(array)): # 对第i个元素进行插入，i前面是已经排序好的元素
 position = i # 要插入数的下标
 current_val = array[position] # 把当前值存下来
 # 如果前一个数大于要插入数，则将前一个数往后移，比如5,8,12,7;要将7插入，先把7保存下来，比较12与7，将12往后移
 while position > 0 and current_val < array[position-1]:
 array[position] = array[position-1]
 position -= 1
 else: # 当position为０或前一个数比待插入还小时
 array[position] = current_val


if __name__ == "__main__":
 array = [92, 77, 67, 8, 6, 84, 55, 85, 43, 67]
 print(array)
 time_start = time.time()
 insertion_sort(array)
 time_end = time.time()
 print("time: %s" % (time_end-time_start))
 print(array)

ログイン後にコピー

输出:

[92, 77, 67, 8, 6, 84, 55, 85, 43, 67]
time: 0.0
[6, 8, 43, 55, 67, 67, 77, 84, 85, 92]

如果碰见一个和插入元素相等的，那么插入元素把想插入的元素放在相等元素的后面。所以，相等元素的前后顺序没有改变，从原无序序列出去的顺序就是排好序后的顺序，所以插入排序是稳定的。

直接插入排序复杂度:

时间复杂度: 最好情况O(n), 最坏情况O(n^2), 平均情况O(n^2)

空间复杂度: O(1)

稳定性: 稳定

个人感觉直接插入排序算法难度是选择/冒泡算法是两倍……

四、快速排序

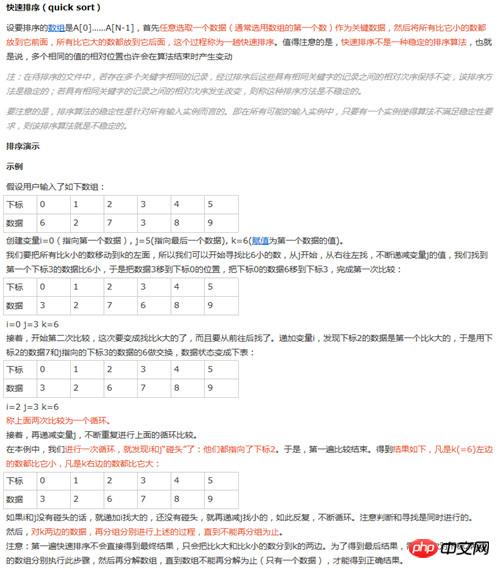
快速排序示例:

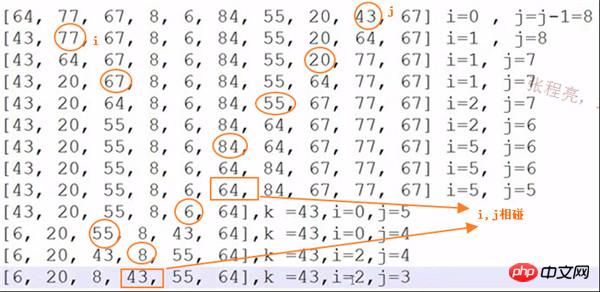
算法实现:

def quick_sort(array, left, right):
 &#39;&#39;&#39;
 :param array:
 :param left: 列表的第一个索引
 :param right: 列表最后一个元素的索引
 :return:
 &#39;&#39;&#39;
 if left >= right:
 return

 low = left
 high = right
 key = array[low] # 第一个值，即基准元素

 while low < high: # 只要左右未遇见
 while low < high and array[high] > key: # 找到列表右边比key大的值 为止
 high -= 1
 # 此时直接 把key跟 比它大的array[high]进行交换
 array[low] = array[high]
 array[high] = key

 while low < high and array[low] <= key: # 找到key左边比key大的值，这里为何是<=而不是<呢？你要思考。。。
 low += 1
 # 找到了左边比k大的值 ,把array[high](此时应该刚存成了key) 跟这个比key大的array[low]进行调换
 array[high] = array[low]
 array[low] = key

 quick_sort(array, left, low-1) # 最后用同样的方式对分出来的左边的小组进行同上的做法
 quick_sort(array,low+1, right) # 用同样的方式对分出来的右边的小组进行同上的做法


if __name__ == &#39;__main__&#39;:
 array = [8,4,1, 14, 6, 2, 3, 9,5, 13, 7,1, 8,10, 12]
 print("-------排序前-------")
 print(array)
 quick_sort(array, 0, len(array)-1)
 print("-------排序后-------")
 print(array)

ログイン後にコピー

输出:

-------排序前-------
[8, 4, 1, 14, 6, 2, 3, 9, 5, 13, 7, 1, 8, 10, 12]
-------排序后-------
[1, 1, 2, 3, 4, 5, 6, 7, 8, 8, 9, 10, 12, 13, 14]

22行那里如果不加＝号，当排序64，77，64是会死循环，此时key=64,　最后的64与开始的64交换，开始的64与本最后的64交换……　无穷无尽

直接插入排序复杂度:

时间复杂度: 最好情况O(nlogn), 最坏情况O(n^2), 平均情况O(nlogn)

下面空间复杂度是看别人博客的，我也不大懂了……改天再研究下。

最优的情况下空间复杂度为：O(logn)；每一次都平分数组的情况

最差的情况下空间复杂度为：O( n )；退化为冒泡排序的情况

稳定性:不稳定

快速排序效果：