Matplotlib は Python の最も有名な描画ライブラリです。この記事では、matplotlib+numpy を使用して塗りつぶしプロット、散布図、棒グラフなどのさまざまな描画を行う方法の例を紹介します。必要な方は等高線図を参照してください。 、ドットプロットと3D図を以下で見てみましょう。
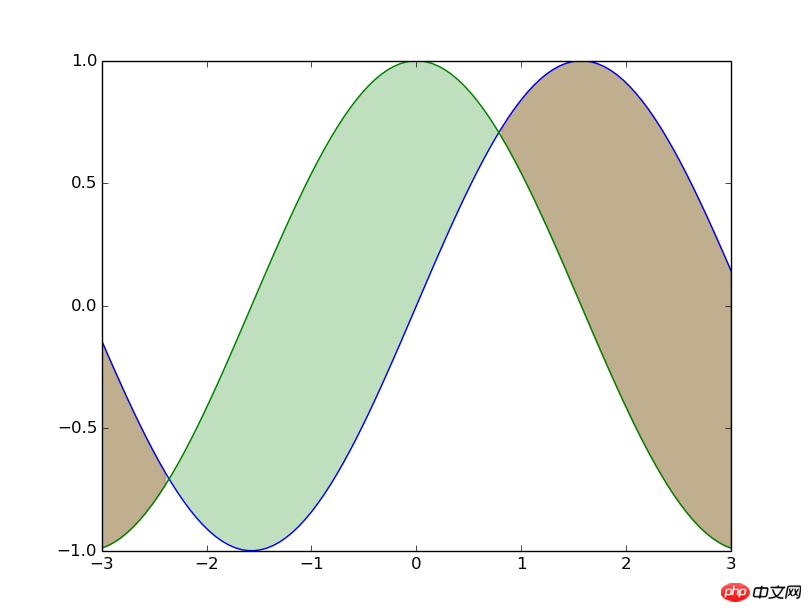
from matplotlib.pyplot import *
x=linspace(-3,3,100)
y1=np.sin(x)
y2=np.cos(x)
fill_between(x,y1,y2,where=(y1>=y2),color='red',alpha=0.25)
fill_between(x,y1,y2,where=(y<>y2),color='green',alpha=0.25)
plot(x,y1)
plot(x,y2)
show()
ログイン後にコピー
と 2 つの y- を渡すことです。 ; 次に、塗りつぶし範囲を渡し、where= を使用して塗りつぶし領域を決定し、最後に塗りつぶしの色、透明度、その他の変更パラメータを追加します。 もちろん、fill_between 関数にはより高度な使用法があります。詳細については、fill_between の使用法またはヘルプ ドキュメントを参照してください。
fill_between函数。这个函数很好理解，就是传入x轴的数组和需要填充的两个y轴数组；然后传入填充的范围，用where=来确定填充的区域；最后可以加上填充颜色啦，透明度之类修饰的参数。
当然fill_between函数还有更加高级的用法，详见fill_between用法或者help文档。
效果图
二、散点图(scatter plots)
参考代码
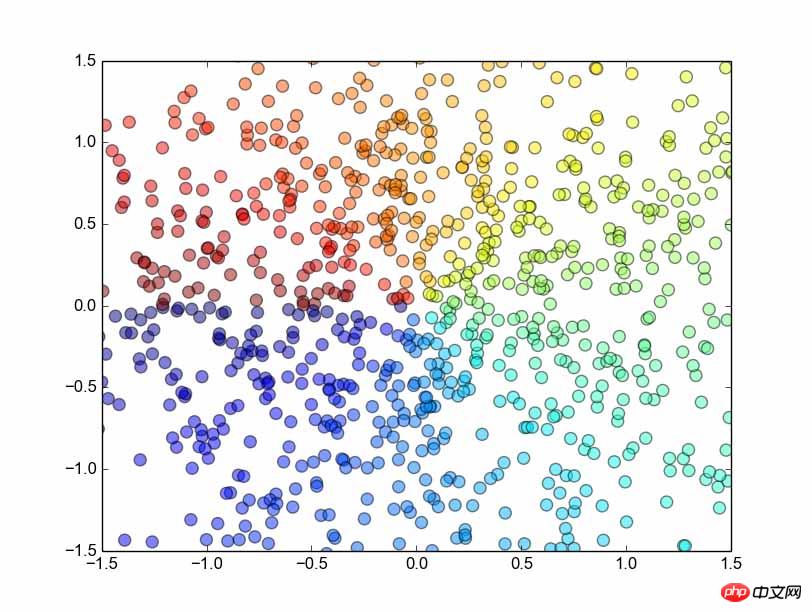
from matplotlib.pyplot import *
n = 1024
X = np.random.normal(0,1,n)
Y = np.random.normal(0,1,n)
T = np.arctan2(Y,X)
scatter(X,Y, s=75, c=T, alpha=.5)
xlim(-1.5,1.5)
ylim(-1.5,1.5)
show()
ログイン後にコピー
简要分析
首先介绍一下numpy 的normal函数，很明显，这是生成正态分布的函数。这个函数接受三个参数，分别表示正态分布的平均值，标准差，还有就是生成数组的长度。很好记。
然后是arctan2函数，这个函数接受两个参数，分别表示y数组和x数组，然后返回对应的arctan(y/x)的值，结果是弧度制。
接下来用到了绘制散点图的scatter方法，首先当然是传入x和y数组，接着s参数表示scale，即散点的大小；c参数表示color，我给他传的是根据角度划分的一个数组，对应的就是每一个点的颜色（虽然不知道是怎么对应的，不过好像是一个根据数组内其他元素进行的相对的转换，这里不重要了，反正相同的颜色赋一样的值就好了）；最后是alpha参数，表示点的透明度。
至于scatter函数的高级用法可以参见官方文档scatter函数或者help文档。
最后设置下坐标范围就好了。
效果图
三、条形图(bar plots)
参考代码
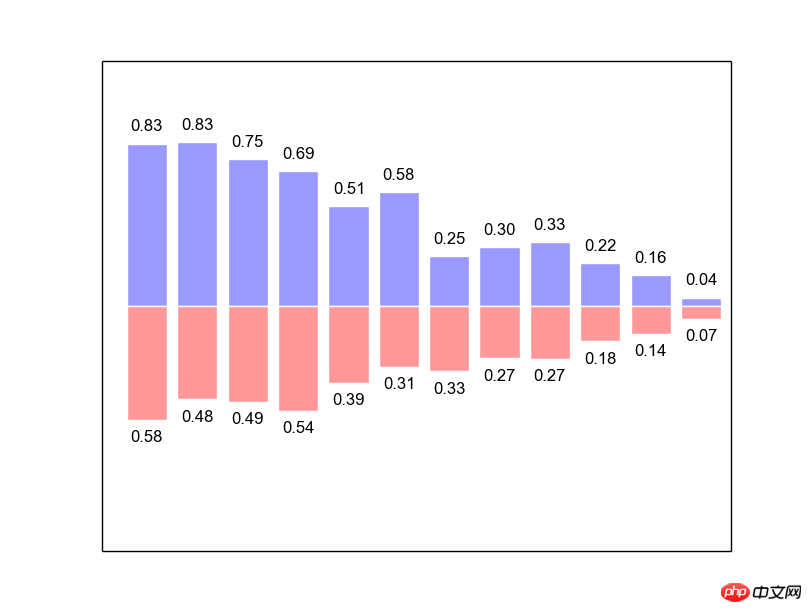
from matplotlib.pyplot import *
n = 12
X = np.arange(n)
Y1 = (1-X/float(n)) * np.random.uniform(0.5,1.0,n)
Y2 = (1-X/float(n)) * np.random.uniform(0.5,1.0,n)
bar(X, +Y1, facecolor='#9999ff', edgecolor='white')
bar(X, -Y2, facecolor='#ff9999', edgecolor='white')
for x,y in zip(X,Y1):
text(x+0.4, y+0.05, '%.2f' % y, ha='center', va= 'bottom')
for x,y in zip(X,Y2):
text(x+0.4, -y-0.05, '%.2f' % y, ha='center', va= 'top')
xlim(-.5,n)
xticks([])
ylim(-1.25,+1.25)
yticks([])
show()
ログイン後にコピー
简要分析
注意要手动导入pylab包，否则会找不到bar。。。
首先用numpy的arange函数生成一个[0,1,2,…,n]的数组。（用linspace也可以）
其次用numpy的uniform函数生成一个均匀分布的数组，传入三个参数分别表示下界、上界和数组长度。并用这个数组生成需要显示的数据。
然后就是bar函数的使用了，基本用法也和之前的plot、scatter类似，传入横纵坐标和一些修饰性参数。
接着我们需要用for循环来为柱状图显示数字：用python的zip函数将X和Y1两两配对并循环遍历，得到每一个数据的位置，然后用text函数在该位置上显示一个字符串（注意位置上的细节调整）。text传入横纵坐标，要显示的字符串，ha参数制定横向对齐，va参数制定纵向对齐。
最后调整下坐标范围，并且取消横纵坐标上的刻度以保持美观即可。
至于barレンダリング
二、散布図
リファレンスコード
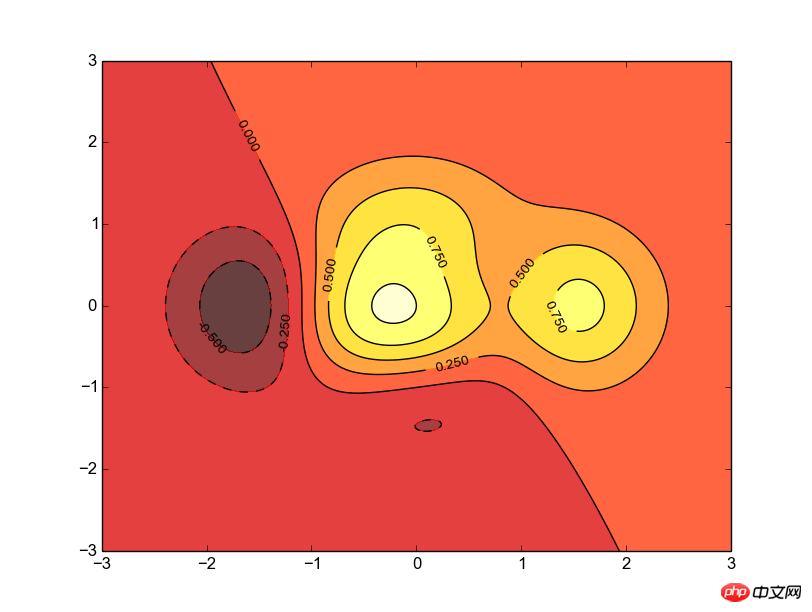
from matplotlib.pyplot import *
def f(x,y):
return (1-x/2+x**5+y**3)*np.exp(-x**2-y**2)
n = 256
x = np.linspace(-3,3,n)
y = np.linspace(-3,3,n)
X,Y = np.meshgrid(x,y)
contourf(X, Y, f(X,Y), 8, alpha=.75, cmap=cm.hot)
C = contour(X, Y, f(X,Y), 8, colors='black', linewidth=.5)
clabel(C, inline=1, fontsize=10)
show()
ログイン後にコピー
ログイン後にコピー
normal関数を紹介します。明らかに、これは正規分布の生成された関数です。この関数は、生成された配列の平均、標準偏差、長さをそれぞれ表す 3 つのパラメーターを受け取ります。とても覚えやすいです。 🎜🎜次に、arctan2 関数があります。この関数は、それぞれ y 配列と x 配列を表す 2 つのパラメーターを受け取り、対応する arctan(y/x) を返します。値と結果はラジアン系です。 🎜🎜次に、散布図を描画するための scatter メソッドが使用されます。もちろん、最初に x 配列と y 配列が渡されます。次に、s パラメーターは散布図のサイズを表します。ポイント; c パラメータは色を表します。彼が渡したものは、各ポイントの色に対応する角度に従って分割された配列でした（どのように対応しているかはわかりませんが、相対的な変換に基づいているようです）。配列内の他の要素については、ここでは重要ではありません。とにかく同じ値を色に割り当てます。最後は、ポイントの透明度を表す alpha パラメーターです。 🎜🎜 scatter 関数の高度な使い方については、公式ドキュメントのスキャッター関数またはヘルプドキュメントを参照してください。 🎜🎜最後に座標範囲を設定するだけです。 🎜🎜🎜レンダリング🎜🎜🎜🎜🎜🎜🎜三、棒グラフ🎜🎜🎜🎜🎜🎜リファレンスコード🎜🎜🎜🎜🎜from matplotlib.pyplot import *
def f(x,y):
return (1-x/2+x**5+y**3)*np.exp(-x**2-y**2)
n = 10
x = np.linspace(-3,3,3.5*n)
y = np.linspace(-3,3,3.0*n)
X,Y = np.meshgrid(x,y)
Z = f(X,Y)
imshow(Z,interpolation='nearest', cmap='bone', origin='lower')
colorbar(shrink=.92)
show()
ログイン後にコピー
ログイン後にコピー
arange 関数を使用して [0,1,2,…,n] の配列を生成します。 (linspace を使用することもできます) 🎜🎜 次に、numpy の uniform 関数を使用して均一に分散された配列を生成し、それぞれ下限、上限、配列の長さを表す 3 つのパラメーターを渡します。そして、この配列を使用して、表示する必要があるデータを生成します。 🎜🎜次に、bar 関数の使用方法について説明します。基本的な使用法は前のプロットと散布図に似ており、水平座標と垂直座標、およびいくつかの装飾パラメーターが渡されます。 🎜🎜次に、for文字列 🎜 (位置の詳細な調整に注意してください)。 text は水平座標と垂直座標、表示される文字列を渡します。ha パラメータは水平方向の配置を指定し、va パラメータは垂直方向の配置を指定します。 🎜🎜最後に座標範囲を調整し、水平方向と垂直方向の座標のスケールを解除して、美しく保ちます。 🎜🎜bar関数の具体的な使い方については、bar関数の使い方やヘルプドキュメントを参照してください。 🎜🎜🎜レンダリング🎜🎜🎜🎜🎜🎜🎜🎜4. 等高線プロット🎜🎜🎜🎜🎜🎜リファレンスコード🎜🎜
from matplotlib.pyplot import *
def f(x,y):
return (1-x/2+x**5+y**3)*np.exp(-x**2-y**2)
n = 256
x = np.linspace(-3,3,n)
y = np.linspace(-3,3,n)
X,Y = np.meshgrid(x,y)
contourf(X, Y, f(X,Y), 8, alpha=.75, cmap=cm.hot)
C = contour(X, Y, f(X,Y), 8, colors='black', linewidth=.5)
clabel(C, inline=1, fontsize=10)
show()
ログイン後にコピー
ログイン後にコピー
简要分析
首先要明确等高线图是一个三维立体图，所以我们要建立一个二元函数f，值由两个参数控制，(注意，这两个参数都应该是矩阵)。
然后我们需要用numpy的meshgrid函数生成一个三维网格，即，x轴由第一个参数指定，y轴由第二个参数指定。并返回两个增维后的矩阵，今后就用这两个矩阵来生成图像。
接着就用到coutourf函数了，所谓contourf，大概就是contour fill的意思吧，只填充，不描边；这个函数主要是接受三个参数，分别是之前生成的x、y矩阵和函数值；接着是一个整数，大概就是表示等高线的密度了，有默认值；然后就是透明度和配色问题了，cmap的配色方案这里不多研究。
随后就是contour函数了，很明显，这个函数是用来描线的。用法可以类似的推出来，不解释了，需要注意的是他返回一个对象，这个对象一般要保留下来个供后续的加工细化。
最后就是用clabel函数来在等高线图上表示高度了，传入之前的那个contour对象；然后是inline属性，这个表示是否清除数字下面的那条线，为了美观当然是清除了，而且默认的也是1；再就是指定线的宽度了，不解释，。
效果图
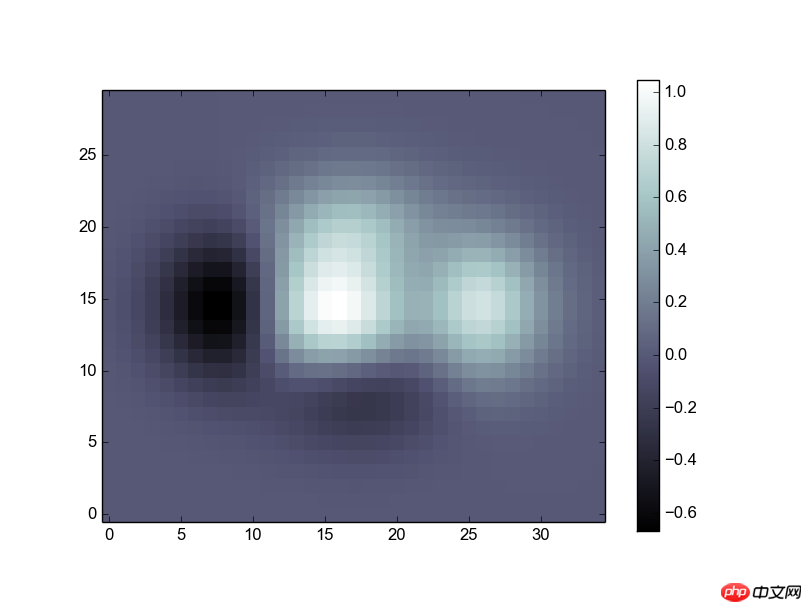
五、点阵图
参考代码
from matplotlib.pyplot import *
def f(x,y):
return (1-x/2+x**5+y**3)*np.exp(-x**2-y**2)
n = 10
x = np.linspace(-3,3,3.5*n)
y = np.linspace(-3,3,3.0*n)
X,Y = np.meshgrid(x,y)
Z = f(X,Y)
imshow(Z,interpolation='nearest', cmap='bone', origin='lower')
colorbar(shrink=.92)
show()
ログイン後にコピー
ログイン後にコピー
简要分析
这段代码的目的就是将一个矩阵直接转换为一张像照片一样的图，完整的进行显示。
前面的代码就是生成一个矩阵Z，不作解释。
接着用到了imshow函数，传人Z就可以显示出一个二维的图像了，图像的颜色是根据元素的值进行的自适应调整，后面接了一些修饰性的参数，比如配色方案（cmap），零点位置（origin）。
最后用colorbar显示一个色条，可以不传参数，这里传进去shrink参数用来调节他的长度。
效果图
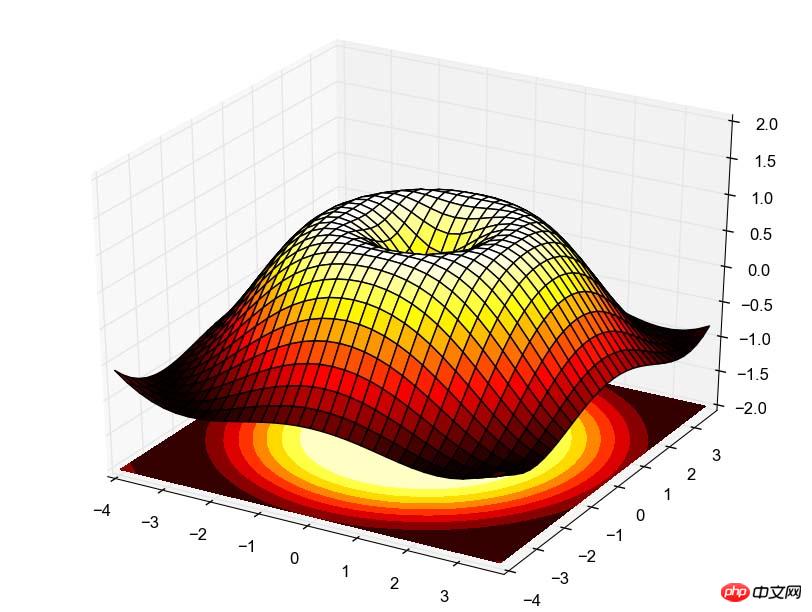
六、３Ｄ图
参考代码
import numpy as np
from pylab import *
from mpl_toolkits.mplot3d import Axes3D
fig = figure()
ax = Axes3D(fig)
X = np.arange(-4, 4, 0.25)
Y = np.arange(-4, 4, 0.25)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=plt.cm.hot)
ax.contourf(X, Y, Z, zdir='z', offset=-2, cmap=plt.cm.hot)
ax.set_zlim(-2,2)
show()
ログイン後にコピー
简要分析
有点麻烦，需要用到的时候再说吧，不过原理也很简单，跟等高线图类似，先画图再描线，最后设置高度，都是一回事。
效果图
总结
【相关推荐】
1. Python免费视频教程
2. Python基础入门教程
3. Python在数据科学中的应用
以上がPythonの描画ライブラリを使った描画方法の紹介の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
![[Web フロントエンド] Node.js クイック スタート](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
