JAVAソートヒープソート
以下のエディターは、比較ソートとヒープソートに関する古い決まり文句を提供します。編集者はこれがとても良いものだと思ったので、皆さんの参考として今から共有します。エディターをフォローして見てみましょう
ヒープのソートには、バイナリ ツリーの完全な知識が必要です。ソートされるシーケンス {10, 2, 11, 8, 7} については、次の図に示すように、完全な二分木とみなします。
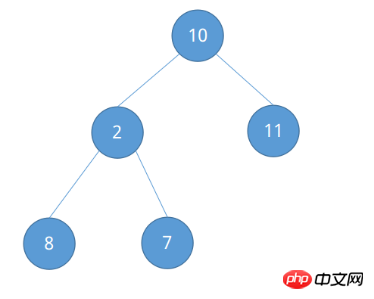
ヒープは、ラージ ルート ヒープとスモール ルート ヒープに分割されます。ラージ ルート ヒープは、各ルート ノードがその子ノードよりも大きいことを意味します (L(i) >= L(2i) && L(i) > = L(2i + 1))、小さなルート ヒープは、各ルート ノードがその子ノードよりも小さいことを意味します (L(i)
この記事では、例として大規模なルート ヒープの構築を使用して説明します。 。
ヒープソートの最初のステップ - 初期ヒープの構築。初期ヒープを構築するにはどうすればよいですか?定義上、キー ポイントは各ルート ノードにあります。ソートされる上記のシーケンスの完全な二分木を観察すると、ノード 2 とノード 10 に注目が必要なノードである子ノードがあることがわかります。
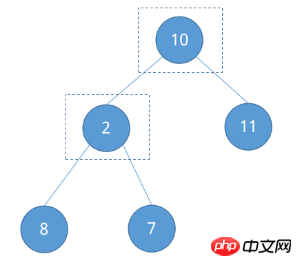
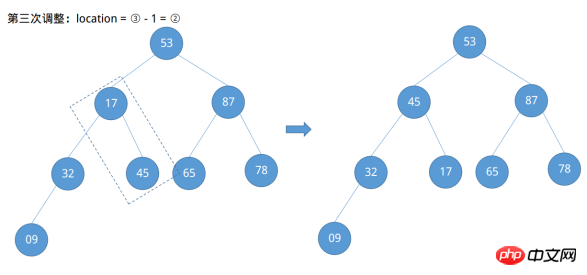
ノード 2 を見つけるには?完全な二分木の性質によれば、それが葉ノード、つまり最後のノードの親ノードであることがわかります。ルート ノードを除くすべてのノードの親ノードの番号は ⌊in / 2⌋ です。 n = 5 とすると、ノード 2 の数は ⌊5 / 2⌋ = ② であることが簡単にわかります。左右の子ノードのサイズと比較して調整します。
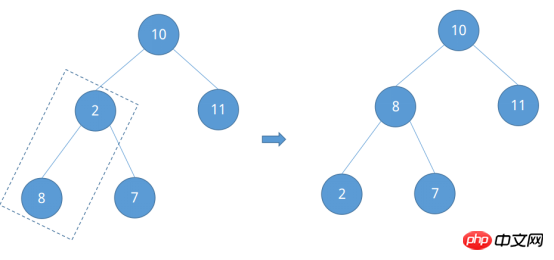
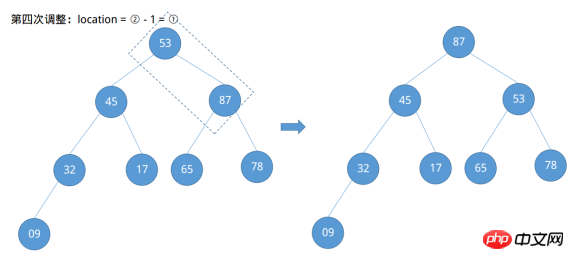
最後にルートノード10が残りますが、ノード2の番号は②、②-1=①であることがわかり、ルートノード10の番号が求まります。左右の子ノードのサイズと比較して調整します。
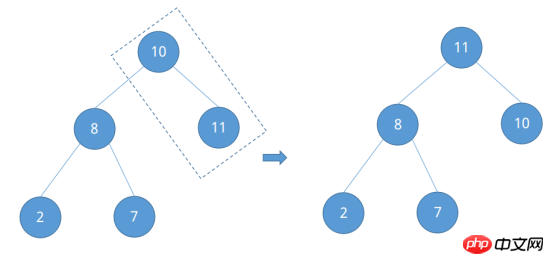
調整が完了すると、「大きなルート ヒープ」が形成されていることがわかります。この例でソートされる列は比較的単純ですが、それを観察するために、より複雑なソートされる列が与えられます。大規模なルート ヒープを構築するプロセス。ソートされるシーケンス {53, 17, 78, 09, 45, 65, 87, 32} の場合、それを完全な二分木として扱います。
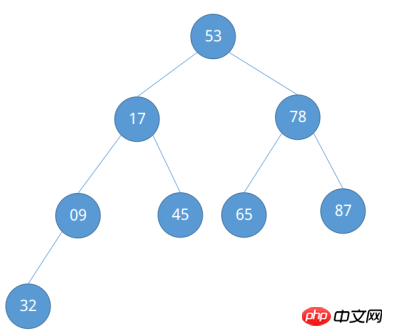
同様に、注意を払う必要があるノードを見てみましょう。
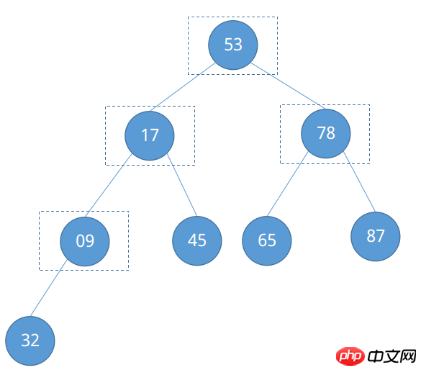
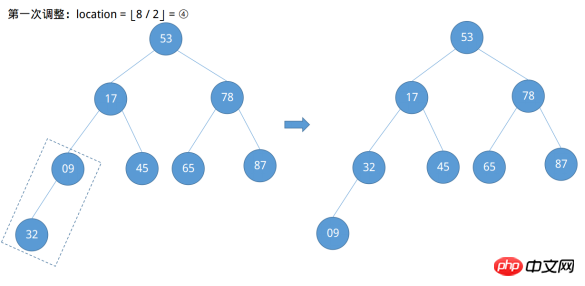
最初の例によれば、ノード 09 の番号は ⌊8 / 2⌋ = ④ として、ノード 78 の番号は ④ - 1 = ③... などとして簡単に見つけることができます。つまり、調整する必要があるノードの位置は ⌊n / 2⌋ からルートノード①が終了するまで (⌊n / 2) 減少します。 ⌋ ~ 1)。今すぐ調整を始めてください。
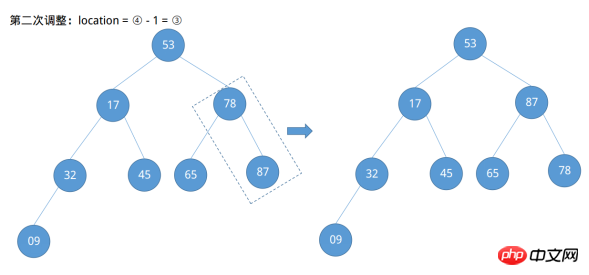
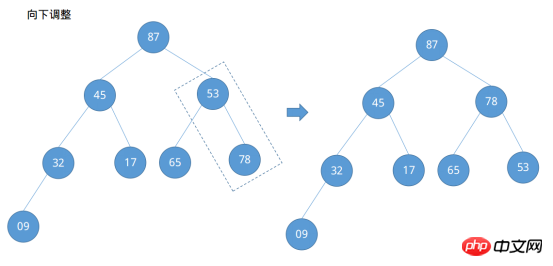
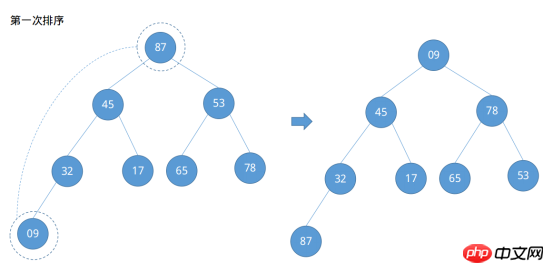
ルートノードと最後のノードを呼び出した後、ソート対象の列の最大値が配列{..., 87}の最後の位置に配置されていることがわかります。このとき、最初のソートは です。ノード 87 を除いて、他のノードは大規模なルート ヒープの条件を満たしていないため、残りのノードは大規模なルート ヒープになるように調整する必要があります。ソート処理は提供されなくなりました。Java および Python3 でのコード実装は次のとおりです。
Java
package com.algorithm.sort.heap;
import java.util.Arrays;
/**
* 堆排序
* Created by yulinfeng on 6/20/17.
*/
public class Heap {
public static void main(String[] args) {
int[] nums = {53, 17, 78, 09, 45, 65, 87, 32};
nums = heapSort(nums);
System.out.println(Arrays.toString(nums));
}
/**
* 堆排序
* @param nums 待排序数组序列
* @return 排好序的数组序列
*/
private static int[] heapSort(int[] nums) {
for (int i = nums.length / 2 - 1; i >= 0; i--) {
heapAdjust(nums, i, nums.length);
}
for (int i = nums.length - 1; i > 0; i--) {
int temp = nums[i];
nums[i] = nums[0];
nums[0] = temp;
heapAdjust(nums, 0, i);
}
return nums;
}
/**
* 调整堆
*
* @param nums 待排序序列
* @param parent 待调整根节点
* @param length 数组序列长度
*/
private static void heapAdjust(int[] nums, int parent, int length) {
int temp = nums[parent];
int childIndex = 2 * parent + 1; //完全二叉树节点i从编号1开始的左子节点位置在2i,此处数组下标从0开始,即左子节点所在数组索引位置为:2i + 1
while (childIndex < length) {
if (childIndex + 1 < length && nums[childIndex] < nums[childIndex + 1]) {
childIndex++; //节点有右子节点,且右子节点大于左子节点,则选取右子节点
}
if (temp > nums[childIndex]) {
break; //如果选中节点大于其子节点,直接返回
}
nums[parent] = nums[childIndex];
parent = childIndex;
childIndex = 2 * parent + 1; //继续向下调整
}
nums[parent] = temp;
}
}Python3
#堆排序
def heap_sort(nums):
for i in range(int(len(nums) / 2 - 1), -1, -1):
heap_adjust(nums, i, len(nums))
for i in range(len(nums) - 1, -1, -1):
temp = nums[i]
nums[i] = nums[0]
nums[0] = temp
heap_adjust(nums, 0, i)
return nums
#调整堆
def heap_adjust(nums, parent, length):
temp = nums[parent]
childIndex = 2 * parent + 1
while childIndex < length:
if childIndex + 1 < length and nums[childIndex] < nums[childIndex + 1]:
childIndex += 1
if temp > nums[childIndex]:
break
nums[parent] = nums[childIndex]
parent = childIndex
childIndex = 2 * parent + 1
nums[parent] = temp
nums = [53, 17, 78, 09, 45, 65, 87, 32]
nums = heap_sort(nums)
print(nums)上記の決まり文句の比較ソートとヒープソートは、すべて編集者が共有した内容であり、参考になれば幸いです。皆さんもスクリプトハウスを応援していただければ幸いです。
以上がJAVAソートヒープソートの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7629
7629
 15
15
 1389
1389
 52
52
 89
89
 11
11
 31
31
 141
141
 ジャワのウェカ
Aug 30, 2024 pm 04:28 PM
ジャワのウェカ
Aug 30, 2024 pm 04:28 PM
Java の Weka へのガイド。ここでは、weka java の概要、使い方、プラットフォームの種類、利点について例を交えて説明します。
 Java Springのインタビューの質問
Aug 30, 2024 pm 04:29 PM
Java Springのインタビューの質問
Aug 30, 2024 pm 04:29 PM
この記事では、Java Spring の面接で最もよく聞かれる質問とその詳細な回答をまとめました。面接を突破できるように。
 Java 8 Stream Foreachから休憩または戻ってきますか?
Feb 07, 2025 pm 12:09 PM
Java 8 Stream Foreachから休憩または戻ってきますか?
Feb 07, 2025 pm 12:09 PM
Java 8は、Stream APIを導入し、データ収集を処理する強力で表現力のある方法を提供します。ただし、ストリームを使用する際の一般的な質問は次のとおりです。 従来のループにより、早期の中断やリターンが可能になりますが、StreamのForeachメソッドはこの方法を直接サポートしていません。この記事では、理由を説明し、ストリーム処理システムに早期終了を実装するための代替方法を調査します。 さらに読み取り:JavaストリームAPIの改善 ストリームを理解してください Foreachメソッドは、ストリーム内の各要素で1つの操作を実行する端末操作です。その設計意図はです
 Java での日付までのタイムスタンプ
Aug 30, 2024 pm 04:28 PM
Java での日付までのタイムスタンプ
Aug 30, 2024 pm 04:28 PM
Java での日付までのタイムスタンプに関するガイド。ここでは、Java でタイムスタンプを日付に変換する方法とその概要について、例とともに説明します。
 カプセルの量を見つけるためのJavaプログラム
Feb 07, 2025 am 11:37 AM
カプセルの量を見つけるためのJavaプログラム
Feb 07, 2025 am 11:37 AM
カプセルは3次元の幾何学的図形で、両端にシリンダーと半球で構成されています。カプセルの体積は、シリンダーの体積と両端に半球の体積を追加することで計算できます。このチュートリアルでは、さまざまな方法を使用して、Javaの特定のカプセルの体積を計算する方法について説明します。 カプセルボリュームフォーミュラ カプセルボリュームの式は次のとおりです。 カプセル体積=円筒形の体積2つの半球体積 で、 R:半球の半径。 H:シリンダーの高さ(半球を除く)。 例1 入力 RADIUS = 5ユニット 高さ= 10単位 出力 ボリューム= 1570.8立方ユニット 説明する 式を使用してボリュームを計算します。 ボリューム=π×R2×H(4
 未来を創る: まったくの初心者のための Java プログラミング
Oct 13, 2024 pm 01:32 PM
未来を創る: まったくの初心者のための Java プログラミング
Oct 13, 2024 pm 01:32 PM
Java は、初心者と経験豊富な開発者の両方が学習できる人気のあるプログラミング言語です。このチュートリアルは基本的な概念から始まり、高度なトピックに進みます。 Java Development Kit をインストールしたら、簡単な「Hello, World!」プログラムを作成してプログラミングを練習できます。コードを理解したら、コマンド プロンプトを使用してプログラムをコンパイルして実行すると、コンソールに「Hello, World!」と出力されます。 Java の学習はプログラミングの旅の始まりであり、習熟が深まるにつれて、より複雑なアプリケーションを作成できるようになります。






