ベジェ曲線の応用を詳しく解説
はじめに
ベジェ曲線は、最初は下に加速して停止し、跳ね上がるときに徐々に減速する、跳ねるボールの複雑なアニメーション効果など、多くの複雑な効果を生成できます。
ベジェ曲線を使用するためによく使用される 2 つの URL は次のとおりです:
イージング関数:
cubic-bezier:
ベジェ曲線を使用して曲線を描画する方法
標準の 3 次ベジェ曲線には 4が必要です> ポイント: 開始点、終了点 (アンカー ポイントとも呼ばれる)、および相互に離れた 2 つの中間点。 4个点:起始点、终止点(也称锚点)以及两个相互分离的中间点。
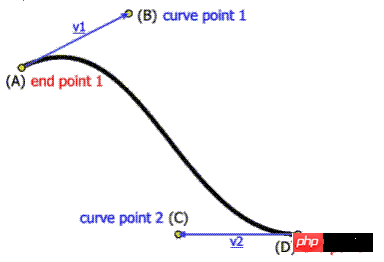
无论SVG, Canvas还是CSS3动画,都牵扯到这4个点。
SVG和贝塞尔曲线的结合
svg可缩放矢量图形(Scalable Vector Graphics)、二维、XML标记,类似下面:
<svg width="160px" height="160px"> <path d="M10 80 ..." /></svg>
SVG的代码不具体展开(说开了可以连载好几篇),提一下其中一个path的标签,可以绘制任意的路径,自然也包括和贝塞尔搞基。
三次贝塞尔曲线指令:C x1 y1, x2 y2, x y两个控制点(x1,y1)和(x2,y2),(x,y)代表曲线的终点。字母C表示特定动作与行为,这里需要大写,表示标准三次方贝塞尔曲线。
看看下面一些描述贝塞尔曲线的代码(片段),大家可以好好地感受下(其中字母M表示特定动作moveTo, 指将绘图的起点移动到此处)。
<svg width="190px" height="160px"> <path d="M10 10 C 20 20, 40 20, 50 10" stroke="3" fill="none"/> <path d="M70 10 C 70 20, 120 20, 120 10" stroke="3" fill="none"/> <path d="M130 10 C 120 20, 180 20, 170 10" stroke="3" fill="none"/> <path d="M10 60 C 20 80, 40 80, 50 60" stroke="3" fill="none"/> <path d="M70 60 C 70 80, 110 80, 110 60" stroke="3" fill="none"/> <path d="M130 60 C 120 80, 180 80, 170 60" stroke="3" fill="none"/> <path d="M10 110 C 20 140, 40 140, 50 110" stroke="3" fill="none"/> <path d="M70 110 C 70 140, 110 140, 110 110" stroke="3" fill="none"/> <path d="M130 110 C 120 140, 180 140, 170 110" stroke="3" fill="none"/></svg>
曲线效果类似下面这张图:

可以看到M后面的起点,加C后面3个点,构成了贝赛尔曲线的4个点。
Canvas与贝塞尔曲线的结合
其中Canvas有个bezierCurveTo()方法,代码如下:
var c=document.getElementById("myCanvas");var ctx=c.getContext("2d");
ctx.beginPath();
ctx.moveTo(20,20);
ctx.bezierCurveTo(20,100,200,100,200,20);
ctx.stroke();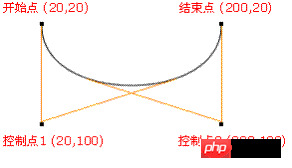
开始点:moveTo(20,20) 控制点 1:bezierCurveTo(20,100,200,100,200,20) 控制点 2:bezierCurveTo(20,100,200,100,200,20) 结束点: bezierCurveTo(20,100,200,100,200,20)
CSS3动画与贝塞尔曲线的结合
用法如下:
transition:cubic-bezier(.25,.1,.25,1)
其中.25,.1这个坐标对于起点连接的那个锚点;.25,1这个坐标对于终点头上那根天线顶端那个点。
有人会疑问,CSS3动画那个cubic-bezier值好像只有两个点诶~~
那是因为CSS3动画贝塞尔曲线的起点和终点已经固定了,分别是(0,0)和(1,1)。
css3中常用的几个动画效果:
ease: cubic-bezier(0.25, 0.1, 0.25, 1.0)
linear: cubic-bezier(0.0, 0.0, 1.0, 1.0)
ease-in: cubic-bezier(0.42, 0, 1.0, 1.0)
ease-out: cubic-bezier(0, 0, 0.58, 1.0)
ease-in-out: cubic-bezier(0.42, 0, 0.58, 1.0)
实现一个弹球的效果:
html代码:
<div id="ball"></div><div id="floor"></div>
css代码:
body{margin:0;padding:0;}#ball{
background:red;
height:100px;
width:100px;
position:absolute;
top:10px;
left:20px;
border-radius:50px;
}#floor{
position:absolute;
bottom:10px;
left:0px;
width:350px;
height:1px;
border-top:5px solid brown;
}js代码:
;(function(){
var down=false,
trans='transition',
eventName='transitionend'; if(typeof document.body.style.webkitTransition==='string'){
trans='webkitTransition';
eventName='webkitTransitionEnd';
}else if(typeof document.body.style.MozTransition==='string'){
trans='MozTransition';
}var ball=document.getElementById('ball');var floor=document.getElementById('floor');function bounce(){ if(down){
ball.style[trans]="Top 1s cubic-bezier(0,.27,.32,1)";
ball.style.top='10px';
down=false;
}else{
ball.style[trans]="Top 1s cubic-bezier(1,0,0.96,0.91)";
ball.style.top=(floor.offsetTop-100)+'px';
down=true;
}
}
ball.addEventListener(eventName,bounce);
bounce();
})();说明:document.body.style.webkitTransition获取以webkit为前缀的transition
在WebKit引擎的浏览器中,当css3的transition动画执行结束时,触发webkitTransitionEnd事件。
实现效果如图所示:

下载地址:《CSS3动画:小球弹跳动画》
总结
canvas:
ctx.moveTo(0,0); ctx.bezierCurveTo(x1,y1,x2,y2,1,1);
SVG:
<path d="M0 0 C x1 y1, x2, y2, 1 1"/>
CSS3贝塞尔起点是0,0; 终点是1, 1
 SVG、Canvas、CSS3 アニメーションに関係なく、それはこの4点です。 🎜🎜SVG とベジェ曲線の組み合わせ🎜🎜svg スケーラブル ベクター グラフィックス (Scalable Vector Graphics)、次のような 2 次元の XML タグ: 🎜🎜
SVG、Canvas、CSS3 アニメーションに関係なく、それはこの4点です。 🎜🎜SVG とベジェ曲線の組み合わせ🎜🎜svg スケーラブル ベクター グラフィックス (Scalable Vector Graphics)、次のような 2 次元の XML タグ: 🎜🎜cubic-bezier(x1,y1, x2,y2)
path タグの 1 つについて触れておきます。このタグは、ベジェによるベースを含む任意のパスを描画できます。 🎜🎜3次ベジェ曲線の命令: C x1 y1, x2 y2, x y2つの制御点 (x1,y1) と (x2,y2) , (x,y) は曲線の終点を表します。文字 C は、特定のアクションと動作を表し、ここでは大文字にする必要があり、標準の 3 次ベジェ曲線を表します。 🎜🎜以下のベジェ曲線を説明するいくつかのコード (フラグメント) を見てください。よく理解できると思います (文字 M は、特定のアクション moveTo を表し、描画 ここに始点が移動します)。 🎜🎜rrreee🎜🎜 カーブ効果は以下の図に似ています: 🎜🎜 🎜🎜
🎜🎜M の後の開始点と、C の後の 3 つの点が、ベジェの 4 点を形成していることがわかります。曲線が🎜🎜Canvas とベジェ曲線の組み合わせ🎜🎜Canvas には bezierCurveTo() メソッドがあり、コードは次のとおりです: 🎜🎜rrreee🎜🎜 🎜🎜Rreeee🎜🎜css3 アニメーションとベッセル曲線。 >.25,.1この座標はアンカー ポイント用です開始点に接続されています。
🎜🎜Rreeee🎜🎜css3 アニメーションとベッセル曲線。 >.25,.1この座標はアンカー ポイント用です開始点に接続されています。.25,1この座標は、終点のアンテナの上部の点です。 🎜🎜CSS3アニメーションのcubic-bezierの値が2点しかないように見えるのではないかと思う人もいるかもしれません~~🎜🎜それはCSS3アニメーションのベジェ曲線の始点と終点が固定されているためです、(0,0) と (1,1) です。 🎜🎜 CSS3 で一般的に使用されるいくつかのアニメーション効果: 🎜🎜ease: cubic-bezier(0.25, 0.1, 0.25, 1.0)linear: cubic-bezier(0.0, 0.0, 1.0, 1.0)
ease - in: cubic-bezier(0.42, 0, 1.0, 1.0)
ease-out: cubic-bezier(0, 0, 0.58, 1.0)
ease-in-out: cubic-bezier(0.42 , 0, 0.58, 1.0)🎜🎜ピンボールの効果を実現する: 🎜🎜html コード: 🎜🎜rrreee🎜🎜css コード: 🎜🎜rrreee🎜🎜js コード: 🎜🎜rrreee🎜🎜説明: document.body.style.webkitTransition は、webkit というプレフィックスが付いたトランジションを取得します
WebKit エンジンのブラウザで、css3 のアニメーションが終了すると、webkitTransitionEnd イベントがトリガーされます。 🎜🎜効果は次の図に示されています: 🎜🎜
 🎜🎜ダウンロードアドレス: "CSS3 アニメーション: ボールバウンスアニメーション"🎜🎜概要🎜🎜canvas:🎜🎜rrreee🎜🎜SVG:🎜🎜rrreee🎜🎜CSS3 ベジェの開始点は0,0; 終点は
🎜🎜ダウンロードアドレス: "CSS3 アニメーション: ボールバウンスアニメーション"🎜🎜概要🎜🎜canvas:🎜🎜rrreee🎜🎜SVG:🎜🎜rrreee🎜🎜CSS3 ベジェの開始点は0,0; 終点は 1, 1;🎜🎜rrreee🎜以上がベジェ曲線の応用を詳しく解説の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7529
7529
 15
15
 1378
1378
 52
52
 81
81
 11
11
 21
21
 76
76
 ブートストラップにスプリットラインを書く方法
Apr 07, 2025 pm 03:12 PM
ブートストラップにスプリットラインを書く方法
Apr 07, 2025 pm 03:12 PM
ブートストラップスプリットラインを作成するには2つの方法があります。タグを使用して、水平方向のスプリットラインを作成します。 CSS Borderプロパティを使用して、カスタムスタイルのスプリットラインを作成します。
 HTML、CSS、およびJavaScriptの役割:コアの責任
Apr 08, 2025 pm 07:05 PM
HTML、CSS、およびJavaScriptの役割:コアの責任
Apr 08, 2025 pm 07:05 PM
HTMLはWeb構造を定義し、CSSはスタイルとレイアウトを担当し、JavaScriptは動的な相互作用を提供します。 3人はWeb開発で職務を遂行し、共同でカラフルなWebサイトを構築します。
 VueでBootstrapの使用方法
Apr 07, 2025 pm 11:33 PM
VueでBootstrapの使用方法
Apr 07, 2025 pm 11:33 PM
vue.jsでBootstrapを使用すると、5つのステップに分かれています。ブートストラップをインストールします。 main.jsにブートストラップをインポートしますブートストラップコンポーネントをテンプレートで直接使用します。オプション:カスタムスタイル。オプション:プラグインを使用します。
 ブートストラップに写真を挿入する方法
Apr 07, 2025 pm 03:30 PM
ブートストラップに写真を挿入する方法
Apr 07, 2025 pm 03:30 PM
ブートストラップに画像を挿入する方法はいくつかあります。HTMLIMGタグを使用して、画像を直接挿入します。ブートストラップ画像コンポーネントを使用すると、レスポンシブ画像とより多くのスタイルを提供できます。画像サイズを設定し、IMG-Fluidクラスを使用して画像を適応可能にします。 IMGボーダークラスを使用して、境界線を設定します。丸い角を設定し、IMGラウンドクラスを使用します。影を設定し、影のクラスを使用します。 CSSスタイルを使用して、画像をサイズ変更して配置します。背景画像を使用して、背景イメージCSSプロパティを使用します。
 ブートストラップのフレームワークをセットアップする方法
Apr 07, 2025 pm 03:27 PM
ブートストラップのフレームワークをセットアップする方法
Apr 07, 2025 pm 03:27 PM
Bootstrapフレームワークをセットアップするには、次の手順に従う必要があります。1。CDNを介してブートストラップファイルを参照してください。 2。独自のサーバーでファイルをダウンロードしてホストします。 3。HTMLにブートストラップファイルを含めます。 4.必要に応じてSASS/LESSをコンパイルします。 5。カスタムファイルをインポートします(オプション)。セットアップが完了したら、Bootstrapのグリッドシステム、コンポーネント、スタイルを使用して、レスポンシブWebサイトとアプリケーションを作成できます。
 ブートストラップボタンの使用方法
Apr 07, 2025 pm 03:09 PM
ブートストラップボタンの使用方法
Apr 07, 2025 pm 03:09 PM
ブートストラップボタンの使用方法は?ブートストラップCSSを導入してボタン要素を作成し、ブートストラップボタンクラスを追加してボタンテキストを追加します
 ブートストラップの日付を表示する方法
Apr 07, 2025 pm 03:03 PM
ブートストラップの日付を表示する方法
Apr 07, 2025 pm 03:03 PM
回答:ブートストラップの日付ピッカーコンポーネントを使用して、ページで日付を表示できます。手順:ブートストラップフレームワークを紹介します。 HTMLで日付セレクター入力ボックスを作成します。ブートストラップは、セレクターにスタイルを自動的に追加します。 JavaScriptを使用して、選択した日付を取得します。





