部分集合和問題の詳細な例
注: 「部分集合と問題」の研究が十分に深くないため、この記事には動的計画法の再帰式の説明に不明確な記述や誤りがある可能性があります。見つけた場合はご指摘いただければ幸いです。
部分集合和問題は次のように説明できます: nの正の整数W=(w1, w2, …, wn)と正の整数を仮定すると、 M 、∑wi=M,i∈I[1] となるような I⊆{1, 2, 3, ..., n}, を見つける必要があります。部分集合和問題の一般的な説明を与える例を取り上げます: 正の整数 M=5 が与えられたとき、集合 W=(1, 2, 3, 4, 5) は存在しますか W のサブセット I。サブセット I 内の要素の合計が M に等しい。この例では、明らかにサブセット I=(2, 3)。
問題の定義: 正の整数W, s[i, j] が与えられた場合、正の整数の集合 S=(w1, w2, w3, …, wn) i は S の部分集合を表し、j は部分集合 i の合計を表します。 Sのある集合iの要素の和j=Mであれば、つまり問題には解があります。
例:S=(7, 34, 4, 12, 5, 3), W=6、Sの部分集合はありますか、その要素の合計は等しいWへ。
この問題には多くの解決策もあります。この記事では、動的計画法の考え方を使用して解決するため、再帰的な公式を導出する必要があります。集合S を継続的に小さな集合に分割します。これが 動的プログラミングの最初のステップです: 部分問題を定義します。集合 S の最小の集合は空集合です。 もちろん、空集合は存在せず、その要素の合計は j=0 に等しいです。空のセットが対象となります。
この表の列は集合内の要素の合計を表しており、最大でも要素Wまでしか到達できませんが、Wより大きい場合はもちろん意味がありません。 j=6列に1が表示されていれば、問題の解が得られます。この行は、最初の i (i を含む) 要素で構成されるサブセットを表します (この文は少し疑わしいかもしれません。すべての状況をスキャンすることは可能ではないでしょうか? それから読み続けてください)。 i=0は空集合を意味します。
j=6のとき、空集合状況は真であると定義します。次に、 j=0 の場合、これは任意の部分集合の合計に当てはまります (空集合はその部分集合です)。したがって、フォームには以下に示すように入力が続けられます。
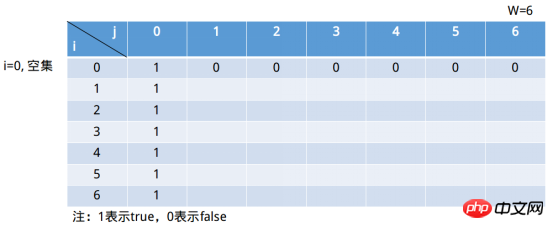
これらは実際には動的プログラミングの 3 番目のステップ、つまり初期状態の定義です。状態計画の 2 番目のステップは、状態遷移ルール、つまり状態間の再帰的な関係を定義することです。
s[i, j]のiは、最初のi部分集合(にはiが含まれる)を表す。実際には、ここから 2 つの部分に分割します:
1)i 番目の要素の最初の i サブセット、つまり s[i - 1, j] を除きます。 ;
2)i 番目の要素の最初の i サブセットが含まれます。
1)の状況では、最初のi - 1集合要素の合計がjに等しい場合、最初のiの部分集合要素が存在することが分かりやすいです。 合計は j に等しい。
理解が難しいのは、2)の状況です。 2 番目のケースについて明らかにできることの 1 つは、s[i,数学で「特別値法」を使用する場合、例えば集合(3, 34, 9)では、要素の合計がに等しい特定のサブセットは存在しますか? 37、この時点では i=2 (サブセットは (3, 34))、j = 37、この時点では " には最初の が含まれますi iサブセットのこの場合、s[2, 37] => s[2, 37 - 34] = s[2, 3]、サブセット(3 , 34) もちろん、要素の合計が 3 に等しい部分集合があります。次に、 j = 36, s[2, 36] => s[2, 36 - 34] = s[2, 2], サブセット (3, 34) 明らかに要素の合計が 2 に等しいサブセットはありません。 j = 1, s[2, 1] => s[2, 1 - 34] = s[2, -32], j - wi < 、このとき s[2, 1] => s[2 - 1, 1] = s[1, 1]、そのサブセット要素の間にサブセット (3) は明らかに存在しません。合計は1となります。 要約すると、再帰式は次のとおりです: このアルゴリズムをコードに実装する前に、まず再帰式を通じて上記の行列を埋めます。 ①i = 1、このときの部分集合は(7)、j = 1
、
j  ∉(∅)
∉(∅)
(i = 0は空集合を表します)。明らかに s[1, 1] = 0 です。 ②i = 1, このときの部分集合は(7), j = 2, j ∉ (∅), 選択状況2) => s[0, 2 ] | s[1, -5] (i = 0 は空集合を意味します)。明らかに s[1, 2] = 0 です。 … I=1、この時点でサブセットは(7)、j=6、j(∅)、選択状況2)=&gtです。 ; s[0, 6] || s[1, -1] (i = 0は空集合を表します)。明らかに s[1, 6] = 0 です。 ①i = 6, (7, 34, 4, 12, 5, 3), j = 1, j ∉ (7, 34, 4, 12, 5), 選択状況 2) => s[5, 1] || s[6, -2] (i = 0は空集合を表します)。明らかに s[6, 1] = 0 です。 ②i = 6, (7, 34, 4, 12, 5, 3), j = 2, j ∉ (7, 34, 4, 12 , 5)、選択状況 2) => s[5, 1] || s[6, -1] (i = 0 は空集合を意味します)。明らかに s[6, 2] = 0 です。 ③i = 6, (7, 34, 4, 12, 5, 3), j = 3, j ∉ (7, 34, 4, 12 , 5)、選択ケース 2) => s[5, 1] ||明らかに s[6, 3] = 1 です。 … ⑥i = 6, (7, 34, 4, 12, 5, 3), j = 6, j ∉ (7, 34, 4, 12) 、 5)、選択状況 2) => s[5, 6] || s[6, 3]。明らかに s[6, 6] = 1 です。 Python3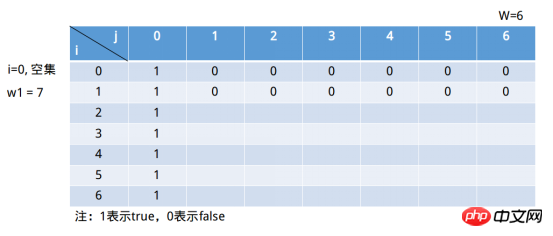 最終的な埋め込みは以下のようになります:
最終的な埋め込みは以下のようになります: 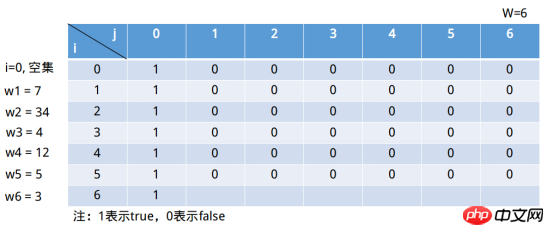 引き続き最後の行を埋めます:
引き続き最後の行を埋めます: 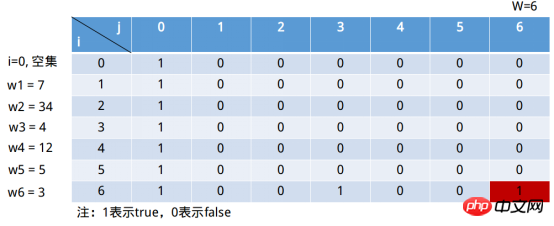
1 package com.algorithm.dynamicprogramming; 2 3 import java.util.Arrays; 4 5 /** 6 * 子集和问题 7 * Created by yulinfeng on 7/2/17. 8 */ 9 public class SubsetSumProblem {10 11 public static void main(String[] srgs) {12 int[] sets = {7, 34, 4, 12, 5, 3};13 int sum = 87;14 boolean isExistSubSet = subsetSumProblem(sets, sum);15 System.out.println("集合" + Arrays.toString(sets) + "是否存在子集的和等于" + sum + ":" + isExistSubSet);16 }17 18 private static boolean subsetSumProblem(int[] sets, int sum) {19 int row = sets.length + 1;20 int col = sum + 1;21 int[][] solutionMatrix = new int[row][col];22 solutionMatrix[0][0] = 1;23 24 /**25 * 0 1 2 3 4 5 626 * 0 |1|0|0|0|0|0|0|27 * 1 |x|x|x|x|x|x|x|28 * 2 |x|x|x|x|x|x|x|29 * 3 |x|x|x|x|x|x|x|30 * 3 |x|x|x|x|x|x|x|31 * 4 |x|x|x|x|x|x|x|32 * 5 |x|x|x|x|x|x|x|33 * 6 |x|x|x|x|x|x|x|34 */35 for (int i = 1; i < col; i++) {36 solutionMatrix[0][i] = 0;37 }38 /**39 * 初始状态40 * 0 1 2 3 4 5 641 * 0 |1|0|0|0|0|0|0|42 * 1 |1|0|x|x|x|x|x|43 * 2 |x|x|x|x|x|x|x|44 * 3 |x|x|x|x|x|x|x|45 * 3 |x|x|x|x|x|x|x|46 * 4 |x|x|x|x|x|x|x|47 * 5 |x|x|x|x|x|x|x|48 * 6 |1|0|0|x|x|x|x|49 * [i][0] = 1,按行填充50 */51 for (int i = 1; i < row; i++) {52 solutionMatrix[i][0] = 1;53 for (int j = 1; j < col; j++) {54 solutionMatrix[i][j] = solutionMatrix[i - 1][j];55 56 if (solutionMatrix[i][j] == 1) {57 solutionMatrix[i][j] = solutionMatrix[i][j];58 } else if ( j - sets[i - 1] >= 0 && solutionMatrix[i][j - sets[i - 1]] == 1) {59 solutionMatrix[i][j] = solutionMatrix[i][j - sets[i - 1]];60 } else {61 solutionMatrix[i][j] = 0;62 }63 64 if (j == col - 1 && solutionMatrix[i][j] == 1) {65 return true;66 }67 }68 }69 70 return false;71 }72 } 1 def subset_sum_problem(sets, sum): 2 row = len(sets) + 1 3 col = sum + 1 4 solutionMatrix = [[0 for col in range(col)] for row in range(row)] 5 solutionMatrix[0][0] = 1 6 for i in range(1, col): 7 solutionMatrix[0][i] = 0 8 9 for j in range(1, row):10 solutionMatrix[j][0] = 111 for k in range(1, col):12 solutionMatrix[j][k] = solutionMatrix[j - 1][k]13 if solutionMatrix[j][k] == 1:14 solutionMatrix[j][k] = solutionMatrix[j][k]15 elif (k - sets[j - 1] >= 0) and (solutionMatrix[j][k - sets[j - 1]] == 1):16 solutionMatrix[j][k] = solutionMatrix[j][k - sets[j - 1]]17 else:18 solutionMatrix[j][k] = 019 if k == col - 1 and solutionMatrix[j][k] == 1:20 return True21 22 return False23 24 sets = [7, 34, 4, 12, 5, 3]25 num = 626 is_exist = subset_sum_problem(sets, num)27 print(is_exist)
以上が部分集合和問題の詳細な例の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7469
7469
 15
15
 1376
1376
 52
52
 77
77
 11
11
 19
19
 29
29
 C++ コードで発生する「エラー: クラス 'ClassName' の再定義」問題を解決する
Aug 25, 2023 pm 06:01 PM
C++ コードで発生する「エラー: クラス 'ClassName' の再定義」問題を解決する
Aug 25, 2023 pm 06:01 PM
C++ コードの「error:redefiningofclass'ClassName'」問題を解決する C++ プログラミングでは、さまざまなコンパイル エラーが頻繁に発生します。よくあるエラーの 1 つは、「error:redefiningofclass 'ClassName'」 (クラス 'ClassName' の再定義エラー) です。このエラーは通常、同じクラスが複数回定義されている場合に発生します。この記事では、
 クラスタリングアルゴリズムにおけるクラスタリング効果評価問題
Oct 10, 2023 pm 01:12 PM
クラスタリングアルゴリズムにおけるクラスタリング効果評価問題
Oct 10, 2023 pm 01:12 PM
クラスタリング アルゴリズムのクラスタリング効果評価問題には、特定のコード例が必要です クラスタリングは、データをクラスタリングすることによって、類似したサンプルを 1 つのカテゴリにグループ化する教師なし学習手法です。クラスタリングアルゴリズムでは、クラスタリングの効果をどのように評価するかが重要な問題となります。この記事では、一般的に使用されるいくつかのクラスタリング効果評価指標を紹介し、対応するコード例を示します。 1. クラスタリング効果評価指標 シルエット係数 シルエット係数は、サンプルの近さや他のクラスタとの分離度を計算することでクラスタリング効果を評価します。
 C# を使用して動的プログラミング アルゴリズムを作成する方法
Sep 20, 2023 pm 04:03 PM
C# を使用して動的プログラミング アルゴリズムを作成する方法
Sep 20, 2023 pm 04:03 PM
C# を使用して動的プログラミング アルゴリズムを作成する方法 概要: 動的プログラミングは、最適化問題を解決するための一般的なアルゴリズムであり、さまざまなシナリオに適しています。この記事では、C# を使用して動的プログラミング アルゴリズムを作成する方法を紹介し、具体的なコード例を示します。 1. 動的プログラミング アルゴリズムとは何ですか? 動的プログラミング (DP) は、重複する部分問題と最適な部分構造特性を持つ問題を解決するために使用されるアルゴリズムのアイデアです。動的プログラミングでは、問題を解決するためのいくつかのサブ問題に分解し、各サブ問題の解決策を記録します。
 iPhone の一般的な問題を診断する方法を教えます
Dec 03, 2023 am 08:15 AM
iPhone の一般的な問題を診断する方法を教えます
Dec 03, 2023 am 08:15 AM
強力なパフォーマンスと多彩な機能で知られる iPhone は、複雑な電子機器によく見られる、時折起こる問題や技術的な困難を免れません。 iPhone の問題が発生するとイライラすることもありますが、通常は警報を発する必要はありません。この包括的なガイドでは、iPhone の使用に関連して最も一般的に遭遇する課題のいくつかをわかりやすく説明することを目的としています。当社の段階的なアプローチは、これらの一般的な問題の解決に役立つように設計されており、機器を最高の動作状態に戻すための実用的な解決策とトラブルシューティングのヒントを提供します。不具合やより複雑な問題に直面している場合でも、この記事はそれらを効果的に解決するのに役立ちます。一般的なトラブルシューティングのヒント 具体的なトラブルシューティング手順を詳しく説明する前に、役立つ情報をいくつか紹介します。
 jQueryがform要素の値を取得できない問題の解決方法
Feb 19, 2024 pm 02:01 PM
jQueryがform要素の値を取得できない問題の解決方法
Feb 19, 2024 pm 02:01 PM
jQuery.val() が使用できない問題を解決するには、具体的なコード例が必要です フロントエンド開発者にとって、jQuery の使用は一般的な操作の 1 つです。その中でも、.val() メソッドを使用してフォーム要素の値を取得または設定する操作は、非常に一般的な操作です。ただし、特定のケースでは、.val() メソッドを使用できないという問題が発生する可能性があります。この記事では、いくつかの一般的な状況と解決策を紹介し、具体的なコード例を示します。問題の説明 jQuery を使用してフロントエンド ページを開発する場合、時々次のような問題が発生します。
 PHP アルゴリズム分析: 動的プログラミング アルゴリズムを使用して最長回文部分文字列問題を解決するにはどうすればよいですか?
Sep 19, 2023 pm 12:19 PM
PHP アルゴリズム分析: 動的プログラミング アルゴリズムを使用して最長回文部分文字列問題を解決するにはどうすればよいですか?
Sep 19, 2023 pm 12:19 PM
PHP アルゴリズム分析: 動的プログラミング アルゴリズムを使用して最長回文部分文字列問題を解決するにはどうすればよいですか?動的計画法 (動的計画法) は、多くの複雑な問題を解決できる、一般的に使用されるアルゴリズムのアイデアです。そのうちの 1 つは、最長回文部分文字列の問題です。これは、文字列内の最長回文部分文字列の長さを見つけることです。この記事では、PHP を使用してこの問題を解決する動的プログラミング アルゴリズムを作成する方法を紹介し、具体的なコード例を示します。まず、最長の回文部分文字列を定義しましょう。回文文字列とは、前から見ても後ろから読んでも同じ文字列を指します。
 C++ でナップザック問題アルゴリズムを使用する方法
Sep 21, 2023 pm 02:18 PM
C++ でナップザック問題アルゴリズムを使用する方法
Sep 21, 2023 pm 02:18 PM
C++ でのナップザック問題アルゴリズムの使用方法 ナップザック問題は、コンピュータ アルゴリズムにおける古典的な問題の 1 つであり、アイテムの合計価値を最大化するために、指定されたナップザック容量の下でナップザックに入れるいくつかのアイテムを選択する方法が含まれます。この記事では、C++ の動的プログラミング アルゴリズムを使用してナップザック問題を解決する方法と、具体的なコード例を詳しく紹介します。まず、ナップサック問題の入力と出力を定義する必要があります。入力には、アイテムの重み配列 wt[]、アイテムの値配列 val[]、およびバックパックの容量 W が含まれます。出力はどのオブジェクトが選択されているかです。
 弱教師学習におけるラベル取得問題
Oct 08, 2023 am 09:18 AM
弱教師学習におけるラベル取得問題
Oct 08, 2023 am 09:18 AM
弱教師あり学習におけるラベル取得問題には、特定のコード例が必要です はじめに: 弱教師あり学習は、トレーニングに弱いラベルを使用する機械学習手法です。従来の教師あり学習とは異なり、弱教師あり学習では、各サンプルに正確なラベルが必要ではなく、より少ないラベルを使用してモデルをトレーニングするだけで済みます。しかし、弱教師あり学習では、弱いラベルから有用な情報をいかに正確に取得するかが重要な問題となります。この記事では、弱教師あり学習におけるラベル取得問題を紹介し、具体的なコード例を示します。弱教師学習におけるラベル獲得問題の紹介:




