バックトラッキング手法サブセット ツリー テンプレートを使用して最長共通部分列問題を取得する Python の詳細な例
この記事では、Python がバックトラッキング法サブセット ツリー テンプレートを使用して最長共通部分列 (LCS) を取得する方法を主に紹介し、最長共通部分列問題について簡単に説明し、Python がバックトラッキング法サブセット ツリー テンプレートを使用してそれを分析する方法について説明します。最長共通部分列を取得するための操作手順と注意事項については、必要な友達は参考にしてください
この記事では、Python を使用してバックトラッキング サブセット ツリー テンプレートを使用して最長共通部分列 (LCS) を取得する方法について説明します。 。参考のために皆さんと共有してください。詳細は次のとおりです:
質問
入力
行 1: 文字列 A
行 2: 文字列 B
(A,B
Output
最長のサブシーケンスが複数ある場合は、任意に 1 つを出力します。
入力例
belong
cnblogs
出力例
blog
分析
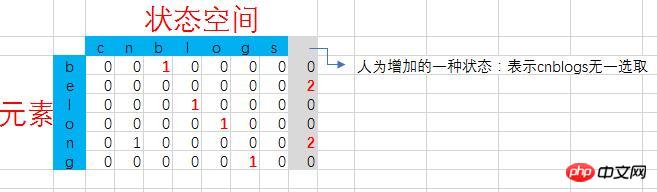
バックトラッキングサブセットツリーテンプレートを適用する予定なので、要素状態を使用する必要があります空間分析方法。
文字列内のより短い長さの文字を要素として使用し、より長い長さの文字列内の文字を状態空間として使用します。要素ごとに、その状態空間をトラバースし、その他のことは枝刈り関数に任せます。 ! !
解決策 x の長さは固定されておらず、xi は文字列 b のシーケンス番号を表します。
各要素を処理するときに、状態が選択されていない (cnblogs 内の文字が選択されていない) 場合、プログラムは次の要素に進むことができません。
これは本当に大変なことです! ! ! 1 日考えた結果、状態空間を拡張して状態 q を追加するという方法をついに見つけました。要素が状態 q を選択する場合、それは正当です。ただし、状態 q は解 x に加算されません。 ! !
直感的な画像を見てください:
さあ、お楽しみください!
コード
'''最长公共子序列'''
# 作者:hhh5460
# 时间:2017年6月3日
a = 'belong'
b = 'cnblogs'
x = [] # 一个解(长度不固定)xi是b中字符的序号
X = [] # 一组解
best_x = [] # 最佳解
best_len = 0 # 最大子序列长度
# 冲突检测
def conflict(k):
global n, x, X, a,b,best_len
# 如果两个字符不相等
if x[-1] < len(b) and a[k] != b[x[-1]]:
return True
# 如果两个字符相等,但是相对于前一个在b中的位置靠前
if a[k] == b[x[-1]] and (len(x) >= 2 and x[-1] <= x[-2]):
return True
# 如果部分解的长度加上后面a剩下的长度,小于等于best_len
if len(x) + (len(a)-k) < best_len:
return True
return False # 无冲突
# 回溯法(递归版本)
def LCS(k): # 到达a中的第k个元素
global x, X,a,b,best_len,best_x
#print(k, x)
if k == len(a): # 超出最尾的元素
if len(x) > best_len:
best_len = len(x)
best_x = x[:]
else:
for i in range(len(b)+1): # 遍历 状态空间:0~len(b)-1,技巧:人为增加一种状态len(b),表示改行没有元素选取
if i==len(b): # 此状态不放入解x内
LCS(k+1)
else:
x.append(i)
if not conflict(k): # 剪枝
LCS(k+1)
x.pop() # 回溯
# 根据一个解x,构造最长子序列lcs
def get_lcs(x):
global b
return ''.join([b[i] for i in x])
# 测试
LCS(0)
print(b)
print(best_x)
print(get_lcs(best_x))レンダリング
以上がバックトラッキング手法サブセット ツリー テンプレートを使用して最長共通部分列問題を取得する Python の詳細な例の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7517
7517
 15
15
 1378
1378
 52
52
 79
79
 11
11
 21
21
 66
66
 Python vs. C:比較されたアプリケーションとユースケース
Apr 12, 2025 am 12:01 AM
Python vs. C:比較されたアプリケーションとユースケース
Apr 12, 2025 am 12:01 AM
Pythonは、データサイエンス、Web開発、自動化タスクに適していますが、Cはシステムプログラミング、ゲーム開発、組み込みシステムに適しています。 Pythonは、そのシンプルさと強力なエコシステムで知られていますが、Cは高性能および基礎となる制御機能で知られています。
 Debian Apacheログを使用してWebサイトのパフォーマンスを向上させる方法
Apr 12, 2025 pm 11:36 PM
Debian Apacheログを使用してWebサイトのパフォーマンスを向上させる方法
Apr 12, 2025 pm 11:36 PM
この記事では、Debianシステムの下でApacheログを分析することにより、Webサイトのパフォーマンスを改善する方法について説明します。 1.ログ分析の基本Apacheログは、IPアドレス、タイムスタンプ、リクエストURL、HTTPメソッド、応答コードなど、すべてのHTTP要求の詳細情報を記録します。 Debian Systemsでは、これらのログは通常、/var/log/apache2/access.logおよび/var/log/apache2/error.logディレクトリにあります。ログ構造を理解することは、効果的な分析の最初のステップです。 2。ログ分析ツールさまざまなツールを使用してApacheログを分析できます。コマンドラインツール:GREP、AWK、SED、およびその他のコマンドラインツール。
 Python:ゲーム、GUIなど
Apr 13, 2025 am 12:14 AM
Python:ゲーム、GUIなど
Apr 13, 2025 am 12:14 AM
PythonはゲームとGUI開発に優れています。 1)ゲーム開発は、2Dゲームの作成に適した図面、オーディオ、その他の機能を提供し、Pygameを使用します。 2)GUI開発は、TKINTERまたはPYQTを選択できます。 TKINTERはシンプルで使いやすく、PYQTは豊富な機能を備えており、専門能力開発に適しています。
 Laravel(PHP)vs。Python:開発環境とエコシステム
Apr 12, 2025 am 12:10 AM
Laravel(PHP)vs。Python:開発環境とエコシステム
Apr 12, 2025 am 12:10 AM
開発環境とエコシステムにおけるLaravelとPythonの比較は次のとおりです。1。Laravelの開発環境は簡単で、PHPと作曲家のみが必要です。 Laravelforgeなどの豊富な範囲の拡張パッケージを提供しますが、拡張パッケージのメンテナンスはタイムリーではない場合があります。 2。Pythonの開発環境もシンプルで、PythonとPIPのみが必要です。エコシステムは巨大で複数のフィールドをカバーしていますが、バージョンと依存関係の管理は複雑な場合があります。
 PHPとPython:2つの一般的なプログラミング言語を比較します
Apr 14, 2025 am 12:13 AM
PHPとPython:2つの一般的なプログラミング言語を比較します
Apr 14, 2025 am 12:13 AM
PHPとPythonにはそれぞれ独自の利点があり、プロジェクトの要件に従って選択します。 1.PHPは、特にWebサイトの迅速な開発とメンテナンスに適しています。 2。Pythonは、データサイエンス、機械学習、人工知能に適しており、簡潔な構文を備えており、初心者に適しています。
 DDOS攻撃検出におけるDebianスニファーの役割
Apr 12, 2025 pm 10:42 PM
DDOS攻撃検出におけるDebianスニファーの役割
Apr 12, 2025 pm 10:42 PM
この記事では、DDOS攻撃検出方法について説明します。 「DebiansNiffer」の直接的なアプリケーションのケースは見つかりませんでしたが、次の方法はDDOS攻撃検出に使用できます:効果的なDDOS攻撃検出技術:トラフィック分析に基づく検出:突然のトラフィックの成長、特定のポートの接続の急増などのネットワークトラフィックの異常なパターンの識別。たとえば、PysharkライブラリとColoramaライブラリと組み合わせたPythonスクリプトは、ネットワークトラフィックをリアルタイムで監視し、アラートを発行できます。統計分析に基づく検出:データなどのネットワークトラフィックの統計的特性を分析することにより
 Nginx SSL証明書更新Debianチュートリアル
Apr 13, 2025 am 07:21 AM
Nginx SSL証明書更新Debianチュートリアル
Apr 13, 2025 am 07:21 AM
この記事では、DebianシステムでNGINXSSL証明書を更新する方法について説明します。ステップ1:最初にCERTBOTをインストールして、システムがCERTBOTおよびPython3-Certbot-Nginxパッケージがインストールされていることを確認してください。インストールされていない場合は、次のコマンドを実行してください。sudoapt-getupdatesudoapt-getinstolcallcertbotthon3-certbot-nginxステップ2:certbotコマンドを取得して構成してlet'sencrypt証明書を取得し、let'sencryptコマンドを取得し、nginx:sudocertbot - nginxを構成します。
 Debian Readdirが他のツールと統合する方法
Apr 13, 2025 am 09:42 AM
Debian Readdirが他のツールと統合する方法
Apr 13, 2025 am 09:42 AM
DebianシステムのReadDir関数は、ディレクトリコンテンツの読み取りに使用されるシステムコールであり、Cプログラミングでよく使用されます。この記事では、ReadDirを他のツールと統合して機能を強化する方法について説明します。方法1:C言語プログラムを最初にパイプラインと組み合わせて、cプログラムを作成してreaddir関数を呼び出して結果をinclude#include#include inctargc、char*argv []){dir*dir; structdireant*entry; if(argc!= 2){(argc!= 2){




