プログラマー向け上級章: ハッシュ テーブルの気質

Zhang Yanpo 氏は 2016 年に Baishan Cloud Technology に入社し、主にオブジェクト ストレージの研究開発、コンピュータ ルーム全体のデータ分散、修理と問題解決を担当しています。 100PB レベルのデータ ストレージを達成するという目標に向けて、彼はチームを率いて、ネットワーク全体の分散ストレージ システムの設計、実装、展開を完了し、「コールド」データと「ホット」データを分離し、コールド データのコストを 1.2 に削減しました。冗長性が 2 倍になります。

Zhang Yanpo 氏は 2006 年から 2015 年まで Sina に勤務し、アーキテクチャ設計、コラボレーション プロセスの策定、コード仕様と実装標準の策定、および Sina Weibo をサポートする Cross-IDC PB レベルのクラウド ストレージ サービスのほとんどの機能実装を担当しました。 、マイクロディスク、ビデオ、SAE、音楽、ソフトウェア ダウンロード、およびその他の Sina 内部ストレージ サービスを担当しました。2015 年から 2016 年まで、彼は Meituan の上級技術専門家として勤務し、クロス コンピューター ルームの 100 PB オブジェクト ストレージ ソリューションを設計しました。同時実行で信頼性の高いマルチコピー レプリケーション戦略、最適化された消去コードにより IO オーバーヘッドを 90% 削減します。

ソフトウェア開発において、ハッシュ テーブルは、n 個のキーを b 個のバケットにランダムに配置して、b 単位空間に n 個のデータを格納することと同等です。

ハッシュテーブルでいくつかの興味深い現象を発見しました:

ハッシュテーブル内のキーの分布パターン

ハッシュテーブル内のキーとバケットの数が同じ場合(n/b=1) :

• 37%のバケットは空です

• 37%のバケットには1つのキーしかありません

• 26%のバケットには複数のキーがあります(ハッシュ競合)

次の図n =b=20 の場合、ハッシュ テーブル内の各バケットのキーの数が直感的に表示されます (キーの数に従ってバケットを並べ替えます):

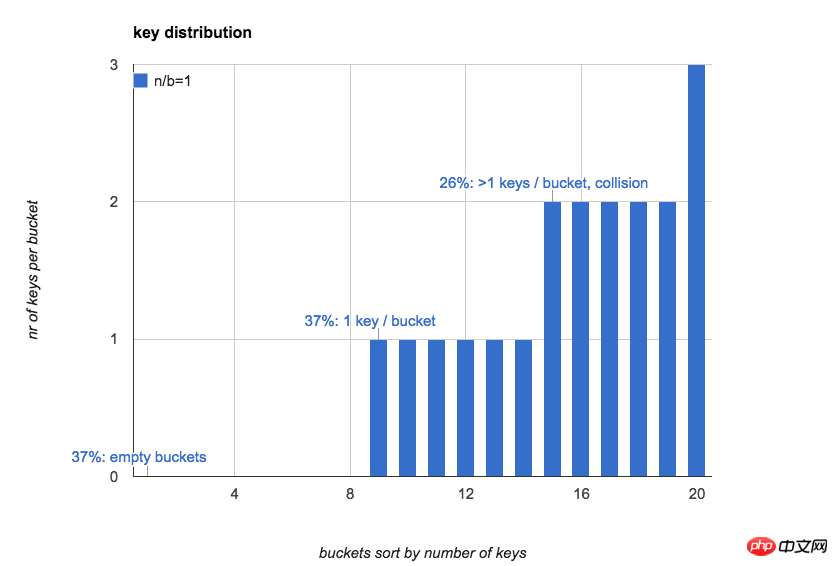
多くの場合、ハッシュ テーブルの第一印象は次のようになります。バケットには比較的均一な数のキーがあり、各バケット内のキーの予想数は 1 です。

実際、n が小さい場合、バケット内のキーの分布は非常に不均一であり、n が増加すると、徐々に平均的になります。

3 つのカテゴリのバケット数に対するキーの数の影響

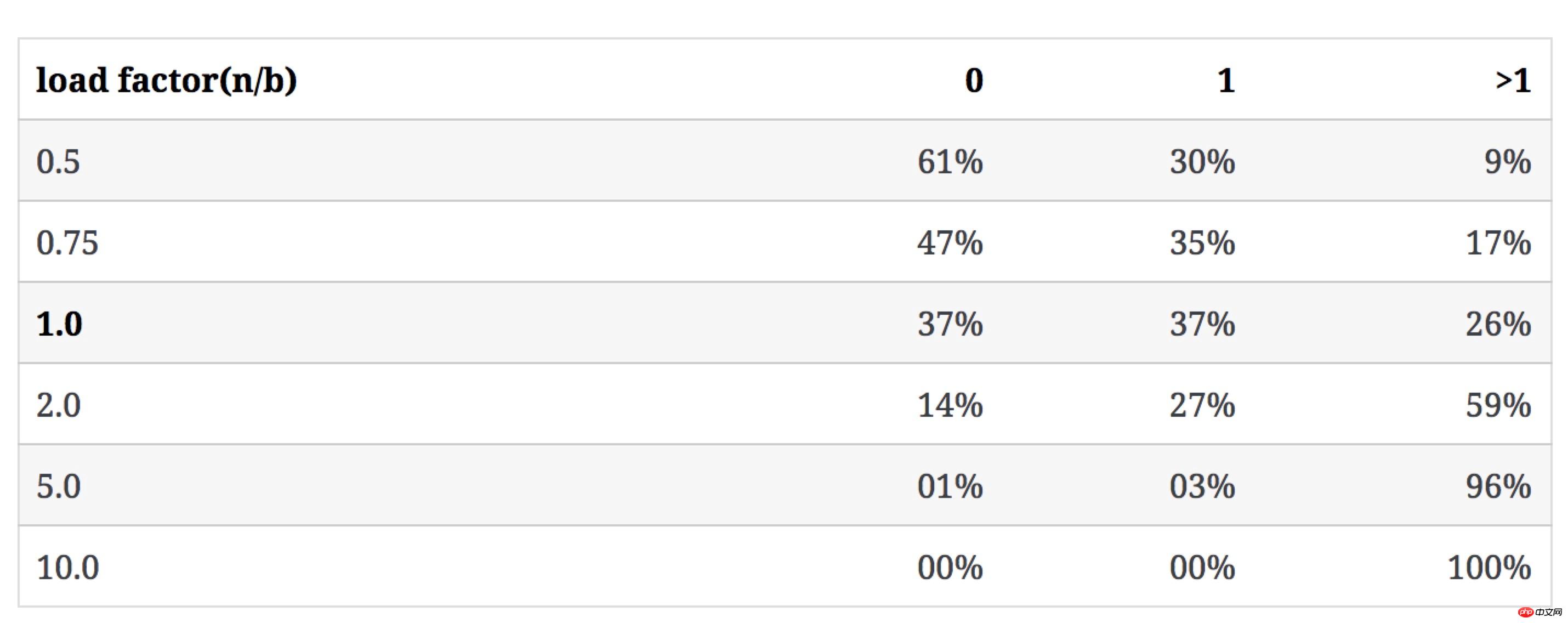
次の表は、b が変化せず、n が増加した場合 (競合レートが 1 キーのバケット比率を超えています):

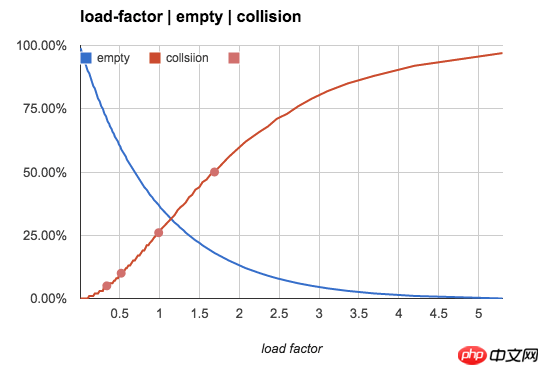
より直観的にするために、次の図を使用して、n/b 値による空のバケット率と競合率の変化傾向を示します:

バケットのキーの数は均等です 程度の影響

上記の数値セットは、n/b が小さい場合には意味のある参考値ですが、n/b が徐々に増加すると、空のバケットの数と 1-キー バケットはほぼ 0 であり、大部分のバケットには複数のキーが含まれています。

n/b が 1 を超える場合 (1 つのバケットに複数のキーを保存できる)、主な観察対象はバケット内のキーの数の分布パターンになります。

次の表は、n/bが大きく、各バケット内のキーの数が均一になる傾向にある場合の偏りの度合いを示しています。
偏りの度合いを表すために、バケット内のキーの最大数と最小数の比 ((最も少ない)/最も多い) を使用して表現します。

次の表は、b=100 の場合に n が増加するにつれてのキーの分布を示しています。

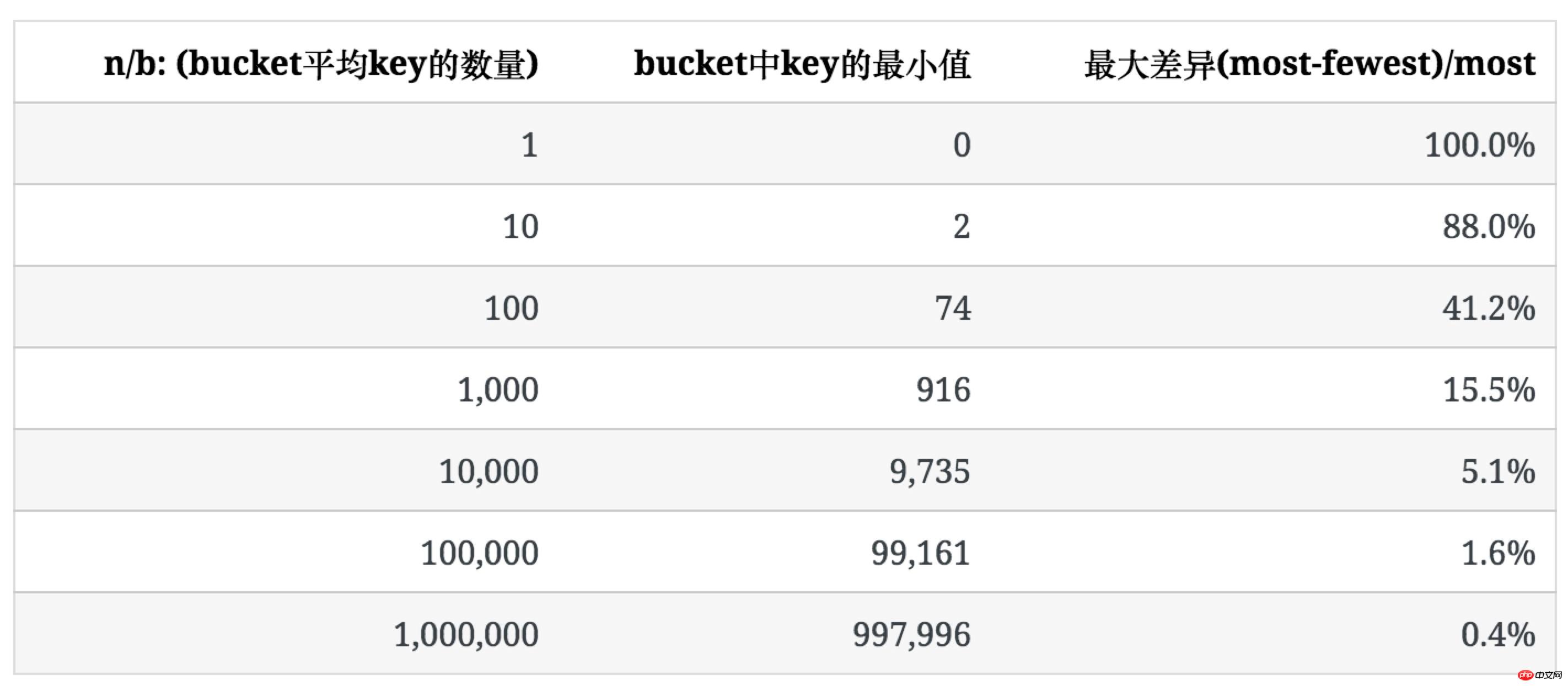
バケット内のキーの平均数が増加するにつれて、その分布の不均一性が徐々に減少することがわかります。

和空bucket或1个key的bucket的占比不同n/b，均匀程度不仅取决于n/b的值，也受b值的影响，后面会提到。

未使用统计中常用的均方差法去描述key分布的不均匀程度，是因为软件开发过程中，更多时候要考虑最坏情况下所需准备的内存等资源。

負荷係数: n/b

ハッシュテーブルで一般的に使用される概念は、ハッシュテーブルの特性を説明するために負荷係数α=n/bです。

通常、メモリストレージハッシュテーブルに基づいて、そのn/b ≤0.75。この設定により、スペースが節約されるだけでなく、キーの競合率が比較的低く保たれるため、ハッシュの再配置の頻度が低くなり、ハッシュ テーブルの挿入が速くなります。

线性探测是一个经常被使用的解决插入时hash冲突的算法，它在1个bucket出现冲突时，按照逐步增加的步长顺序向后查看这个bucket后面的bucket，直到找到1个空bucket。因此它对hash的冲突非常敏感。

n/b=0.75 のこのシナリオでは、線形検出が使用されていない場合 (バケット内のリンク リストを使用して複数のキーを保存するなど)、線形検出が使用されている場合はバケットの約 47% が空になります。 47% バケットの約半分が線形検出によって満たされます。

在很多内存hash表的实现中，选择n/b＝<p><strong>ハッシュ テーブル機能のヒント: </strong></p>

• ハッシュ テーブル自体は、効率を高めるために一定量のスペースを交換するアルゴリズムです。低い時間オーバーヘッド (O(1))、低いスペース無駄、および低い競合率を同時に達成することはできません。

• ハッシュ テーブルは、純粋なメモリ データ構造のストレージにのみ適しています。ハッシュ テーブルはスペースを渡します 無駄はアクセス速度の向上と交換されます。ディスク スペースの無駄は許容できませんが、少量のメモリの無駄は許容されます。
  

ハッシュ テーブルは、高速なランダム アクセスを持つストレージ メディアにのみ適しています。ハードディスク上のデータ ストレージでは、主に btree またはその他の順序付けされたデータ構造が使用されます。
• ほとんどの高級言語 (組み込みハッシュテーブル、ハッシュセットなど) は n/b≤
n/b の場合、ハッシュテーブルはキーを均等に配布しません。小さいです。

Load Factor：n/b>1

另外一种hash表的实现，专门用来存储比较多的key，当 n/b>1n/b1.0时，线性探测失效（没有足够的bucket存储每个key)。这时1个bucket里不仅存储1个key，一般在一个bucket内用chaining，将所有落在这个bucket的key用链表连接起来，来解决冲突时多个key的存储。

链表只在n/b不是很大时适用。因为链表的查找需要O(n)的时间开销，对于非常大的n/b，有时会用tree替代链表来管理bucket内的key。

n/b值较大的使用场景之一是：将一个网站的用户随机分配到多个不同的web-server上，这时每个web-server可以服务多个用户。多数情况下，我们都希望这种分配能尽可能均匀，从而有效利用每个web-server资源。

这就要求我们关注hash的均匀程度。因此，接下来要讨论的是，假定hash函数完全随机的，均匀程度根据n和b如何变化。

n/b 越大，key的分布越均匀

当 n/b 足够大时，空bucket率趋近于0，且每个bucket中key的数量趋于平均。每个bucket中key数量的期望是：

avg=n/b

定义一个bucket平均key的数量是100%：bucket中key的数量刚好是n/b，下图分别模拟了 b=20，n/b分别为 10、100、1000时，bucket中key的数量分布。

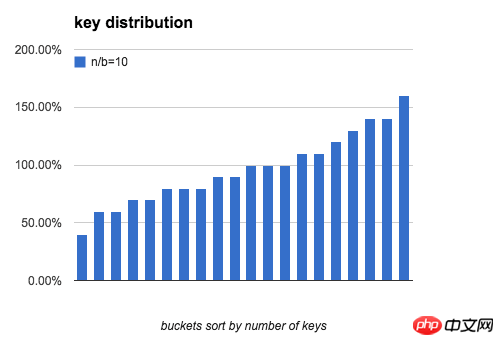
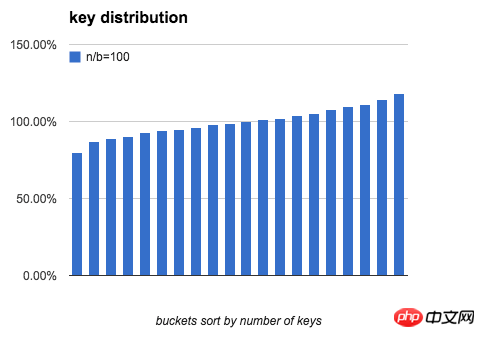
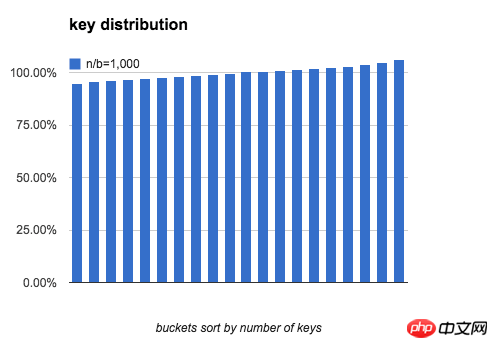
可以看出，当 n/b 增大时，bucket中key数量的最大值与最小值差距在逐渐缩小。下表列出了随b和n/b增大，key分布的均匀程度的变化：

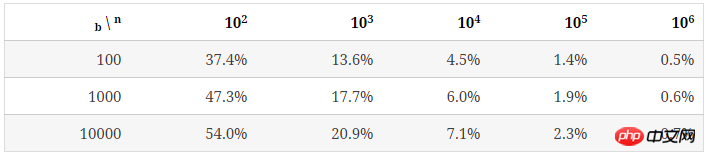
结论:

计算

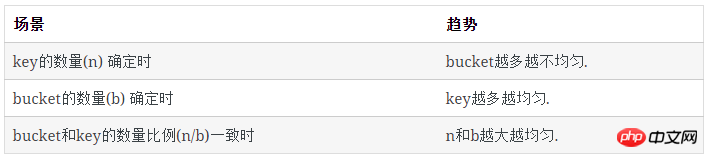
上述大部分结果来自于程序模拟，现在我们来解决从数学上如何计算这些数值。

每类bucket的数量

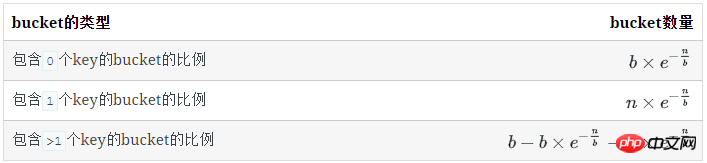
空bucket数量

对于1个key, 它不在某个特定的bucket的概率是 (b−1)/b
所有key都不在某个特定的bucket的概率是( (b−1)/b)n

已知：

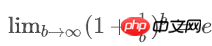
空bucket率是：

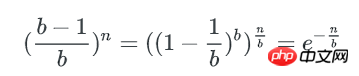
空bucket数量为：

有1个key的bucket数量

n个key中，每个key有1/b的概率落到某个特定的bucket里，其他key以1-(1/b)的概率不落在这个bucket里，因此，对某个特定的bucket，刚好有1个key的概率是：

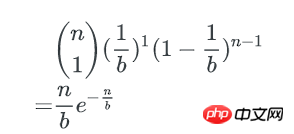
刚好有1个key的bucket数量为：

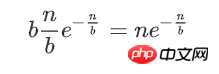
多个key的bucket

剩下即为含多个key的bucket数量：

key在bucket中分布的均匀程度

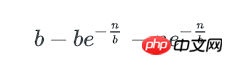
类似的，1个bucket中刚好有i个key的概率是：n个key中任选i个，并都以1/b的概率落在这个bucket里，其他n-i个key都以1-1/b的概率不落在这个bucket里，即：

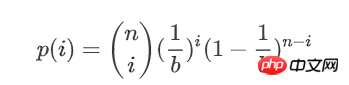
这就是著名的二项式分布。

我们可通过二项式分布估计bucket中key数量的最大值与最小值。

通过正态分布来近似

当 n, b 都很大时，二项式分布可以用正态分布来近似估计key分布的均匀性：

p=1/b，1个bucket中刚好有i个key的概率为：

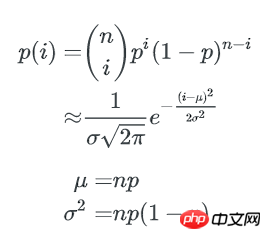
1个bucket中key数量不多于x的概率是：

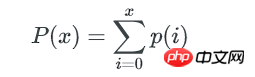
所以，所有不多于x个key的bucket数量是：

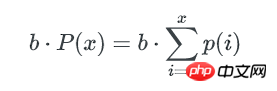
bucket中key数量的最小值，可以这样估算: 如果不多于x个key的bucket数量是1，那么这唯一1个bucket就是最少key的bucket。我们只要找到1个最小的x，让包含不多于x个key的bucket总数为1, 这个x就是bucket中key数量的最小值。

计算key数量的最小值x

一个bucket里包含不多于x个key的概率是：

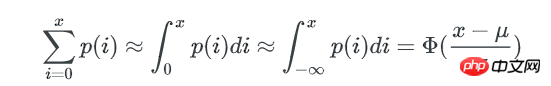
Φ(x) 是正态分布的累计分布函数，当x-μ趋近于0时，可以使用以下方式来近似：

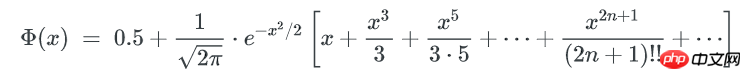
这个函数的计算较难，但只是要找到x，我们可以在[0~μ]的范围内逆向遍历x，以找到一个x 使得包含不多于x个key的bucket期望数量是1。

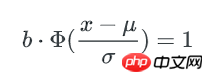
x可以认为这个x就是bucket里key数量的最小值，而这个hash表中，不均匀的程度可以用key数量最大值与最小值的差异来描述: 因为正态分布是对称的，所以key数量的最大值可以用 μ + (μ-x) 来表示。最终，bucket中key数量最大值与最小值的比例就是：

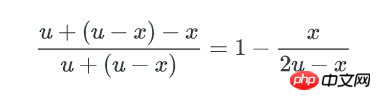
（μ是均值n/b）

程序模拟

以下python脚本模拟了key在bucket中分布的情况，同时可以作为对比，验证上述计算结果。

import sysimport mathimport timeimport hashlibdef normal_pdf(x, mu, sigma):
    x = float(x)
    mu = float(mu)

    m = 1.0 / math.sqrt( 2 * math.pi ) / sigma
    n = math.exp(-(x-mu)**2 / (2*sigma*sigma))return m * ndef normal_cdf(x, mu, sigma):
    # integral(-oo,x)

    x = float(x)
    mu = float(mu)
    sigma = float(sigma)    # to standard form
    x = (x - mu) / sigma

    s = x
    v = x    for i in range(1, 100):
        v = v * x * x / (2*i+1)
        s += v    return 0.5 + s/(2*math.pi)**0.5 * math.e ** (-x*x/2)def difference(nbucket, nkey):

    nbucket, nkey= int(nbucket), int(nkey)    # binomial distribution approximation by normal distribution
    # find the bucket with minimal keys.
    #
    # the probability that a bucket has exactly i keys is:
    #   # probability density function
    #   normal_pdf(i, mu, sigma)
    #
    # the probability that a bucket has 0 ~ i keys is:
    #   # cumulative distribution function
    #   normal_cdf(i, mu, sigma)
    #
    # if the probability that a bucket has 0 ~ i keys is greater than 1/nbucket, we
    # say there will be a bucket in hash table has:
    # (i_0*p_0 + i_1*p_1 + ...)/(p_0 + p_1 + ..) keys.
    p = 1.0 / nbucket
    mu = nkey * p
    sigma = math.sqrt(nkey * p * (1-p))

    target = 1.0 / nbucket
    minimal = mu    while True:

        xx = normal_cdf(minimal, mu, sigma)        if abs(xx-target) < target/10:            break

        minimal -= 1

    return minimal, (mu-minimal) * 2 / (mu + (mu - minimal))def difference_simulation(nbucket, nkey):

    t = str(time.time())
    nbucket, nkey= int(nbucket), int(nkey)

    buckets = [0] * nbucket    for i in range(nkey):
        hsh = hashlib.sha1(t + str(i)).digest()
        buckets[hash(hsh) % nbucket] += 1

    buckets.sort()
    nmin, mmax = buckets[0], buckets[-1]    return nmin, float(mmax - nmin) / mmaxif __name__ == "__main__":

    nbucket, nkey= sys.argv[1:]

    minimal, rate = difference(nbucket, nkey)    print &#39;by normal distribution:&#39;
    print &#39;     min_bucket:&#39;, minimal    print &#39;     difference:&#39;, rate

    minimal, rate = difference_simulation(nbucket, nkey)    print &#39;by simulation:&#39;
    print &#39;     min_bucket:&#39;, minimal    print &#39;     difference:&#39;, rate

以上がプログラマー向け上級章: ハッシュ テーブルの気質の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。