js はデータ構造を実装します: ツリーとバイナリ ツリー、バイナリ ツリーのトラバーサルと基本的な操作方法

ツリー構造は、非常に重要なタイプの非線形構造です。直感的には、ツリー構造は分岐関係によって定義される階層構造です。

ツリーはコンピュータ分野でも広く使用されています。たとえば、コンパイラでは、ツリーはソース プログラムの文法構造を表すために使用され、データベース システムでは、アルゴリズムの動作を分析するときに使用されます。ツリーは、その実行プロセスなどを記述するために使用できます。

まず、ツリーのいくつかの概念を見てみましょう: 1. ツリー (ツリー) は、n (n>=0) 個のノードの有限集合です。空ではないツリーでは:

(1) ルートと呼ばれる特定のノードが 1 つだけ存在します

(2) n>1 の場合、残りのノードは互いに素な有限集合 m(m>0) に分割できます。 T1、T2、T3、...Tm、それぞれはそれ自体がツリーであり、ルートのサブツリーと呼ばれます。

たとえば、(a) はルート ノードが 1 つだけあるツリー、(b) は 13 個のノードを持つツリーで、A がルートで、残りのノードは 3 つの互いに素なサブセットに分割されます: T1={B ,E ,F,K,L},t2={D,H,I,J,M};T1、T2、および T3 はすべてルート A のサブツリーであり、それ自体がツリーです。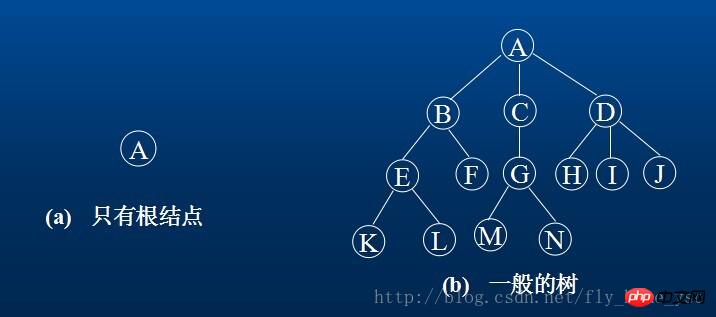

2. ツリーのノードには、データ要素とそのサブツリーを指すいくつかの枝が含まれています。ノードが持つ部分木の数をノードの次数と呼びます。たとえば、(b) では、A の次数は 3、C の次数は 1、F の次数は 0 です。次数 0 のノードはリーフまたはターミナル ノードと呼ばれます。次数が 0 以外のノードは、非終端ノードまたは分岐ノードと呼ばれます。ツリーの次数は、ツリー内の各ノードの最大次数です。 (b) のツリーの次数は 3 です。ノードのサブツリーのルートはノードの子と呼ばれます。同様に、このノードは子の親と呼ばれます。同じ両親から生まれた子供たちはお互いを兄弟と呼びます。ノードの祖先は、ルートからノードまでの分岐上のすべてのノードです。逆に、あるノードをルートとするサブツリー内のノードは、そのノードの子孫と呼ばれます。

3. ノードのレベルはルートから開始して定義され、ルートが第 1 レベルとなり、次の子が第 2 レベルになります。ノードがレベル l にある場合、そのサブツリーのルートはレベル l+1 にあります。親が同じレベルにあるノードは互いにいとこです。たとえば、ノード G と E、F、H、I、および J は互いにいとこです。ツリー内のノードの最大レベルは、ツリーの深さまたは高さと呼ばれます。 (b) のツリーの深さは 4 です。

4. ツリー内のノードのサブツリーが左から右に順序付けされていると見なされる場合 (つまり、交換できない場合)、そのツリーは順序付きツリーと呼ばれ、そうでない場合は順序なしツリーと呼ばれます。順序付きツリーでは、一番左のサブツリーのルートは最初の子と呼ばれ、一番右のサブツリーのルートは最後の子と呼ばれます。

5. フォレストは、m (m>=0) 個の互いに素な木の集合です。ツリー内の各ノードのサブツリーのセットがフォレストです。

バイナリ ツリーに関連する概念を見てみましょう:

バイナリ ツリーは、別のツリー構造です。その特徴は、各ノードに最大 2 つのサブツリーがあることです (つまり、バイナリ ツリーには次数が 2 を超えるノードはありません)。 .点)、二分木の部分木は左右の部分木に分けることができます(順序を任意に逆転することはできません)

二分木の性質:

1. 上には最大で 2 つの i-1 乗ノードがあります。二分木の i 番目のレベル (i>=1)。

2. 深さ k の二分木は、最大で 2 k 乗 - 1 個のノードを持ちます (k>=1)。

3. 任意の二分木 T について、終端ノードの数が n0、次数 2 のノードの数が n2 であれば、n0 = n2 + 1;

深さ k と 2 の k 乗の木- ノードが 1 つのバイナリ ツリーをフル バイナリ ツリーと呼びます。

深さ k の n 個のノードを持つバイナリ ツリーは、その各ノードが深さ k の完全なバイナリ ツリーの 1 から n までの番号が付けられたノードに対応する場合にのみ、完全であると呼ばれます。

以下は完全な二分木の 2 つの特性です:

4. n 個のノードを持つ完全な二分木の深さは Math.floor(log 2 n) + 1

5. n 個のノードを持つ木の場合、ノード完全なバイナリ ツリー (深さは Math.floor(log 2 n) + 1) に順番に番号が付けられます (第 1 レベルから Math.floor(2 n) + 1 まで、各レベルは左から右へ)。 、任意のノード (11 の場合、その親のparent(i)はノード Math.floor(i/2) です。

(2) 2i > n の場合、ノード i には左の子がありません (ノード i は葉ノードです); それ以外の場合、その左の子 LChild(i) はノード 2i です。 > n の場合、ノード i には右側の子がありません。それ以外の場合、その右側の子 RChild(i) は、バイナリ ツリーのストレージ構造です

1. 順次ストレージ構造
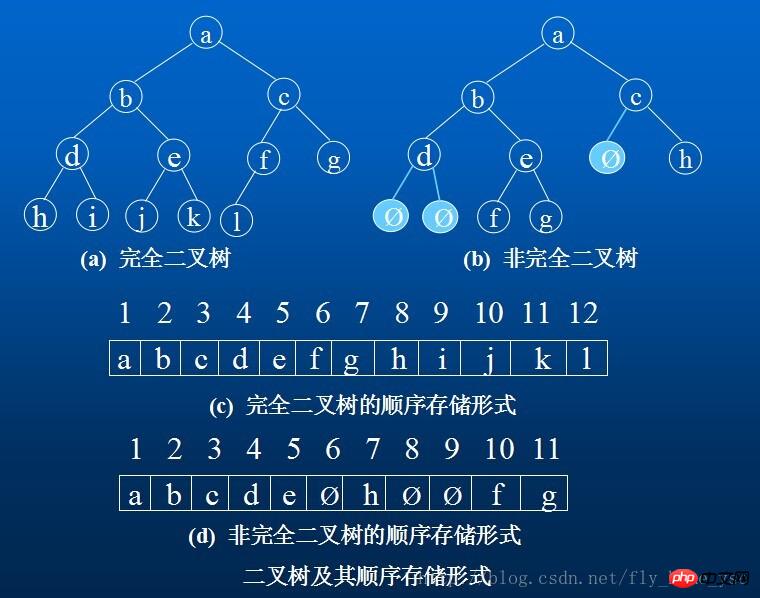
一連の連続ストレージ ユニットを使用して、完全なバイナリ ツリー上でノード要素を上から下、左から右に格納します。つまり、バイナリ ツリー上の i 番号のノード要素は、次元配列の添字 i-1 を持つコンポーネントで定義されます。 「0」は、このノードが存在しないことを意味します。この順次ストレージ構造は、完全なバイナリ ツリーにのみ適しています。
最悪の場合、深さが k でノードが k 個だけの単一ツリー (ツリー内に次数 2 のノードがない) では、長さ 2 の n 乗 -1 の一次元配列が必要になるためです。

2. リンクされたストレージ構造
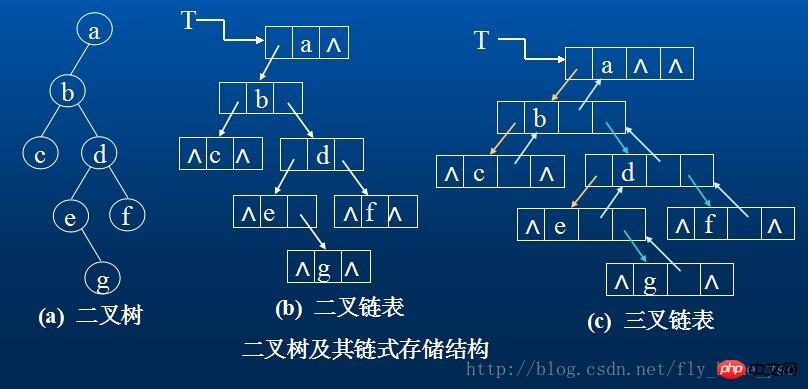
バイナリ ツリーのノードは、データ要素とその左と右のサブツリーをそれぞれ指す 2 つのブランチで構成されます。これは、バイナリ ツリーのリンク リスト内のノードには少なくとも 3 つのフィールドが含まれることを意味します。データフィールドと左右のポインタ領域。場合によっては、ノードの親を見つけやすくするために、その親ノードを指すポインター フィールドをノード構造に追加できます。これら 2 つの構造を使用して得られる二分木の格納構造を、それぞれバイナリ リンク リスト、トリプル リンク リストと呼びます。
n 個のノードを含むバイナリ リンク リストには、n+1 個の空のリンク フィールドがあり、これらの空のリンク フィールドを使用して他の有用な情報を保存し、それによって別のリンクされたストレージ構造、つまり手がかりリンク リストを取得できます。

バイナリ ツリー トラバーサルには、主に 3 つのタイプがあります:

最初 (ルート) 次数トラバーサル: 左と右のルート
中位 (ルート) 次数トラバーサル: 左ルート右
最終 (ルート) 次数トラバーサル: 左と右ルート

二分木の逐次記憶構造:

二分木のリンクされた記憶形式:

// 顺序存储结构
    var tree = [1, 2, 3, 4, 5, , 6, , , 7];
    // 链式存储结构
    function BinaryTree(data, leftChild, rightChild) {
        this.data = data || null;
        // 左右孩子结点
        this.leftChild = leftChild || null;
        this.rightChild = rightChild || null;
    }

二分木の走査 (走査二分木): に従って、二分木の各ノードを 1 回だけ訪問することを指します。指定されたルール。

1. バイナリツリーのプレオーダートラバース

1) アルゴリズムの再帰的定義は次のとおりです:

バイナリツリーが空の場合、トラバースは終了します

⑴ ルートノードにアクセスします

⑵ left subtree (再帰的にこのアルゴリズムを呼び出します);

⑶ 右のサブツリーを順番に走査します (このアルゴリズムを再帰的に呼び出します)。

アルゴリズムの実装:

// 顺序存储结构的递归先序遍历
    var tree = [1, 2, 3, 4, 5, , 6, , , 7];    console.log('preOrder:');
    void function preOrderTraverse(x, visit) {
        visit(tree[x]);
        if (tree[2 * x + 1]) preOrderTraverse(2 * x + 1, visit);
        if (tree[2 * x + 2]) preOrderTraverse(2 * x + 2, visit);
    }(0, function (value) {
        console.log(value);
    });
    // 链式存储结构的递归先序遍历
    BinaryTree.prototype.preOrderTraverse = function preOrderTraverse(visit) {
        visit(this.data);
        if (this.leftChild) preOrderTraverse.call(this.leftChild, visit);
        if (this.rightChild) preOrderTraverse.call(this.rightChild, visit);
    };

2) 非再帰アルゴリズム:

T がバイナリ ツリーのルート ノードを指す変数であると仮定します。非再帰アルゴリズムは次のとおりです。バイナリ ツリーが空の場合は、それ以外の場合は戻ります。 let p=T;

( 1) p はルートノードです;

(2) p が空でない場合、またはスタックが空でない場合は、p が指すノードにアクセスします。 、p がスタックにプッシュされます、p = p .leftChild、左のサブツリーにアクセスします

(4) それ以外の場合は、スタックを p にポップバックし、p = p.rightChild、右のサブツリーにアクセスします

(5) Goスタックが空になるまで (2) に進みます。

コード実装:

// 链式存储的非递归先序遍历

    // 方法1
    BinaryTree.prototype.preOrder_stack = function (visit) {        
    var stack = new Stack();        
    stack.push(this);        
    while (stack.top) {            
    var p;            // 向左走到尽头
            while ((p = stack.peek())) {
                p.data && visit(p.data);                
                stack.push(p.leftChild);
            }            
            stack.pop();            
            if (stack.top) {
                p = stack.pop();                
                stack.push(p.rightChild);
            }
        }
    };    // 方法2
     BinaryTree.prototype.preOrder_stack2 = function (visit) {        
     var stack = new Stack();        
     var p = this;        
     while (p || stack.top) {            
     if (p) {                
     stack.push(p);
                p.data && visit(p.data);
                p = p.leftChild;
            } else {
                p = stack.pop();
                p = p.rightChild;
            }
        }
    };

2. バイナリツリーの順序トラバース:

1) アルゴリズムの再帰定義は次のとおりです:

バイナリツリーが空の場合、トラバースは終了します。左側のサブツリーの順序走査 (このアルゴリズムを再帰的に呼び出します)

⑵ ルートノードにアクセスします

⑶ 右側のサブツリーを順序どおりに走査します (このアルゴリズムを再帰的に呼び出します)。

// 顺序存储结构的递归中序遍历
    var tree = [1, 2, 3, 4, 5, , 6, , , 7];    
    console.log('inOrder:');
    void function inOrderTraverse(x, visit) {        
    if (tree[2 * x + 1]) inOrderTraverse(2 * x + 1, visit);
        visit(tree[x]);
        if (tree[2 * x + 2]) inOrderTraverse(2 * x + 2, visit);
    }(0, function (value) {
        console.log(value);
    });

    // 链式存储的递归中序遍历
    BinaryTree.prototype.inPrderTraverse = function inPrderTraverse(visit) {        
    if (this.leftChild) inPrderTraverse.call(this.leftChild, visit);
        visit(this.data);
        if (this.rightChild) inPrderTraverse.call(this.rightChild, visit);
    };

2) 非再帰アルゴリズム

Tはバイナリツリーのルートノードを指す変数です。 非再帰アルゴリズムは次のとおりです。バイナリツリーが空の場合は、p=T

とします。 p が空でない場合、p はスタックを進めます、p=p.leftChild; ⑵ それ以外の場合 (つまり、p が空である場合)、スタックを p にポップバックし、p が指すノードにアクセスします、p=p.rightChild; ⑶(1)へ

スタックが空になるまで。

<br/>

3. バイナリツリーのポストオーダートラバース:

1) 再帰アルゴリズム

バイナリツリーが空の場合、トラバースは終了します

<br/> ⑴ 左のサブツリーのポストオーダートラバース（このアルゴリズムを呼び出します）再帰的に);

⑵ 事後処理 右のサブツリーをトラバースします (このアルゴリズムを再帰的に呼び出します)

⑶ ルートノードにアクセスします。

// 方法1
    inOrder_stack1: function (visit) {        
    var stack = new Stack();        
    stack.push(this);        
    while (stack.top) {            
    var p;            // 向左走到尽头
            while ((p = stack.peek())) {                
            stack.push(p.leftChild);
            }            
            stack.pop();            
            if (stack.top) {
                p = stack.pop();
                p.data && visit(p.data);                
                stack.push(p.rightChild);
            }
        }
    },    // 方法2
    inOrder_stack2: function (visit) {        
    var stack = new Stack();        
    var p = this;        
    while (p || stack.top) {            
    if (p) {                
    stack.push(p);
                p = p.leftChild;
            } else {
                p = stack.pop();
                p.data && visit(p.data);
                p = p.rightChild;
            }
        }
    },

2) 非再帰アルゴリズム

ポストオーダートラバーサルでは、ルートノードが最後に訪問されるノードになります。したがって、走査プロセス中に、検索ポインタが特定のルート ノードを指している場合、そのルート ノードにすぐにアクセスすることはできませんが、最初にその左側のサブツリーを走査し、ルート ノードをスタックにプッシュする必要があります。左側のサブツリーを走査した後でルート ノードを検索しても、ルート ノードにはまだアクセスできないため、右側のサブツリーを走査する必要があります。したがって、ルート ノードは、その右側のサブツリーが走査されてスタックに戻されるときに、再度スタックにプッシュされ、アクセスできるようにする必要があります。 したがって、ステータス フラグ変数 mark を設定します。

Mark=0 は、このノードがアクセスされたばかりであることを意味し、mark=1 は、左側のサブツリーが処理されて返されたことを意味し、

<br/>mark=2 は、右側のサブツリーが処理されて返されたことを意味します処理されて返送されました。毎回、スタック最上位のマークフィールドに基づいてアクションが決定されます

アルゴリズム実装アイデア:

(1) ルートノードがスタックにプッシュされ、マーク = 0;

(2) Ifスタックが空ではない場合、ノードにポップします

(3) ノードのマーク = 0 の場合、現在のノードのマークを 1 に変更し、左のサブツリーをスタックにプッシュします

(4)ノードのマーク = 1、現在のノードのマークを 2 に変更し、右のサブツリーをスタックに配置します

(5) ノードのマーク = 2 の場合、現在のノードの値にアクセスします。

⑥スタックが空になるまで終了。

// 顺序存储结构的递归后序遍历
    var tree = [1, 2, 3, 4, 5, , 6, , , 7];    
    console.log('postOrder:');
    void function postOrderTraverse(x, visit) {        
    if (tree[2 * x + 1]) postOrderTraverse(2 * x + 1, visit);
        if (tree[2 * x + 2]) postOrderTraverse(2 * x + 2, visit);
        visit(tree[x]);
    }(0, function (value) {
        console.log(value);
    });
    // 链式存储的递归后序遍历
    BinaryTree.prototype.postOrderTraverse = function postOrderTraverse(visit) {        
    if (this.leftChild) postOrderTraverse.call(this.leftChild, visit);
        if (this.rightChild) postOrderTraverse.call(this.rightChild, visit);
        visit(this.data);
    };

具体例

postOrder_stack: function (visit) {
        var stack = new Stack();        
        stack.push([this, 0]);        
        while (stack.top) {
            var a = stack.pop();
            var node = a[0];            
            switch (a[1]) {                
            case 0:                    
            stack.push([node, 1]);  // 修改mark域
                    if (node.leftChild) stack.push([node.leftChild, 0]);  // 访问左子树
                    break;                
                    case 1:                    
                    stack.push([node, 2]);                    
                    if (node.rightChild) stack.push([node.rightChild, 0]);                    
                    break;                
                    case 2:
                    node.data && visit(node.data);                    
                    break;                
                    default:                    
                    break;
            }
        }
    }

以上がjs はデータ構造を実装します: ツリーとバイナリ ツリー、バイナリ ツリーのトラバーサルと基本的な操作方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。