
この記事では、主に JavaScript でよく使用される基本的な並べ替えアルゴリズムを詳しく紹介します。興味のある方は参考にしてください。
注: 内容のほとんどはインターネットからコピーしたもので、コードは私が手書きしたものです。それは単なる過去の復習と新しい知識であり、独創性ではありません。
1. バブルソート
(1) アルゴリズムの説明
バブルソートは単純なソートアルゴリズムです。ソート対象のシーケンスを繰り返し調べて、一度に 2 つの要素を比較し、順序が間違っている場合はそれらを交換します。配列を訪問する作業は、それ以上の交換が必要なくなるまで繰り返されます。これは、配列がソートされたことを意味します。このアルゴリズムの名前は、小さい要素がスワッピングによって配列の先頭にゆっくりと「浮動」するという事実に由来しています。
(2) アルゴリズムの説明と実装
具体的なアルゴリズムは次のように説明されます:
。隣接する要素を比較します。最初の要素が 2 番目の要素よりも大きい場合は、両方の要素を交換します。 先頭の最初のペアから最後の要素まで、同じことを行います。これは最大の数値である必要があります。 を除くすべての要素に対して上記の手順を繰り返します。並べ替えが完了するまで手順 1 ~ 3 を繰り返します。
JavaScript コードの実装:

バブルソートの改善: 各ソートパスでの最後の交換の位置を記録するためにアイコン変数 pos を設定します。 pos 位置以降のレコードは所定の位置で交換されているため、次の並べ替えパスでは pos 位置のみをスキャンする必要があります。
改良されたアルゴリズムは次のとおりです:

従来のバブルソートでは、各ソート操作で最大値または最小値を 1 つだけ見つけることができます。このメソッドは、各ソートパスで順方向バブルと逆方向バブルを使用することを考慮しています。 (最大と最小)を一度に行うことで、ソートパスの数がほぼ半分に減ります。
改善されたアルゴリズムは次のとおりです:

3 つのアルゴリズムの実行時間は次のとおりです:
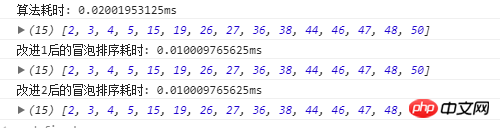
実行結果から、時間の複雑さが低くなり、消費時間が短縮されていることがわかります。実行時に 3 つのアルゴリズムを 1 つのファイルに記述するのが最善です。そうしないと、ブラウザーなどの理由でエラーが発生します。
バブルソートの動的ダイアグラムデモンストレーション:
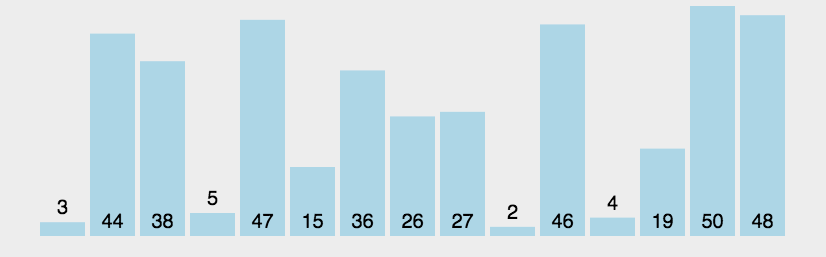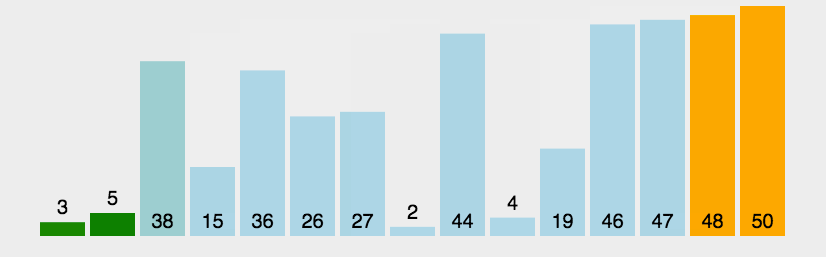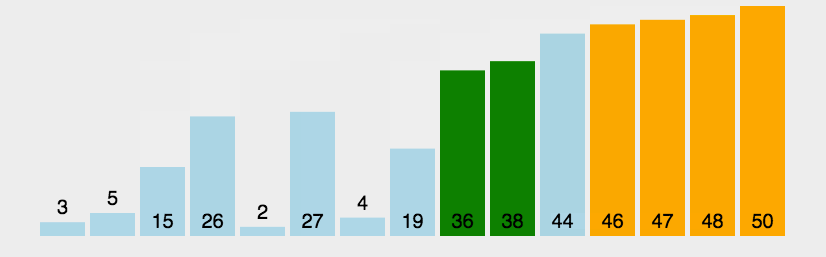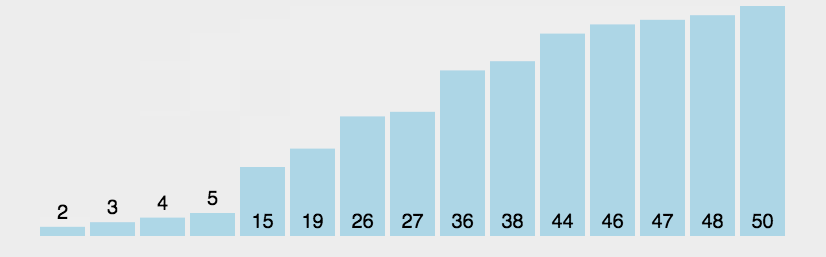
(3) アルゴリズム分析
ベストケース: T(n) = O(n)
入力データがすでに正の順序である場合
ワーストケース: T (n) = O(n2)
入力データが逆順の場合
平均的な状況: T(n) = O(n2)
2. 選択ソート
安定したソートの一つアルゴリズムでは、どのようなデータが入力されても、時間計算量は O(n²) であるため、使用する場合はデータ サイズが小さいほど優れています。唯一の利点は、追加のメモリ領域を占有しないことです。理論的に言えば、選択ソートは、ほとんどの人がソートの際に考える最も一般的なソート方法でもあります。
(1) アルゴリズムの紹介
Selection-sort は、シンプルで直感的な並べ替えアルゴリズムです。仕組み: まず、ソートされていないシーケンス内で最小の (大きい) 要素を見つけて、ソートされたシーケンスの開始位置に格納します。次に、ソートされていない残りの要素から最小の (大きい) 要素を見つけて配置します。ソートされたシーケンスの最後に。すべての要素がソートされるまで続きます。
(2) アルゴリズムの説明と実装
n レコードの直接選択ソートは、n-1 個の直接選択ソート パスを通じて順序付けされた結果を取得できます。具体的なアルゴリズムは次のように説明されます:
。初期状態: 順序付けされていない領域は R[1..n]、順序付けされた領域は空です (i=1)。 ,2,3 ...n-1) 初めに、現在の順序付き領域と順序なし領域はそれぞれ R[1..i-1] と R(i..n) です。このソート操作では、現在の不規則領域から最小のキーを持つレコード R[k] が選択され、それが不規則領域の最初のレコード R と交換され、R[1..i] と R[i+1 .. n)それぞれ、レコード数が1増加した新たな順序付け領域と、レコード数が1減少した新たな非順序付け領域となる。n−1パスが終了し、配列が順序付けされる。
Javascriptコード実装:
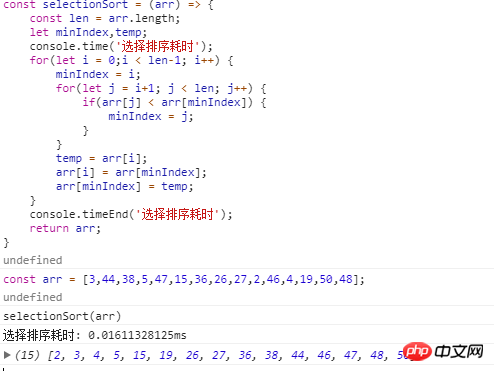
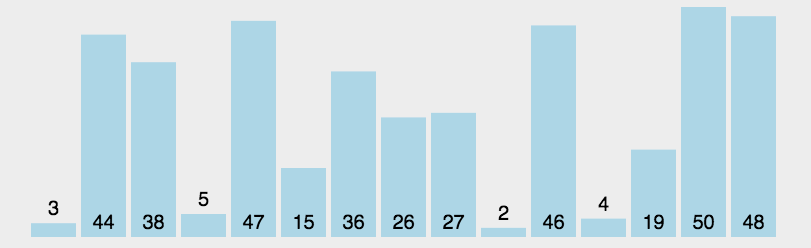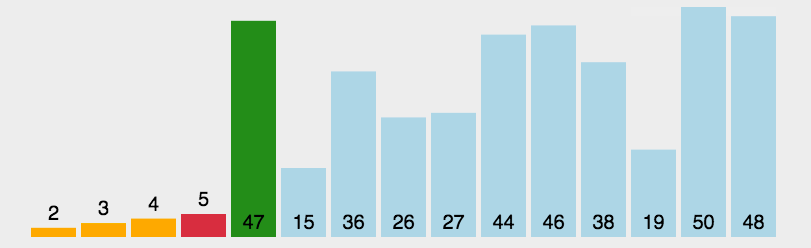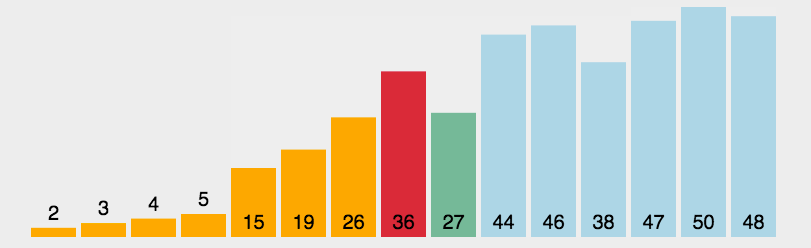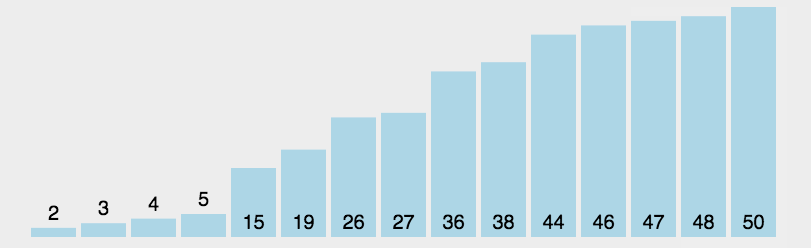
(3)アルゴリズム分析
ベストケース: T(n) = O(n2) ワーストケース: T(n) = O(n2) 平均ケース: T( n) = O(n2)
以上がJavaScript で一般的に使用される基本的な並べ替えアルゴリズムの分析例の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。