クイックソートの実装方法

クイックソート方法

HTML5 Academy-Coder: 「アルゴリズムの旅」の前号で、バブルソート方法と選択ソート方法を共有しました。どちらも時間計算量が O(n^) で「遅い」です。 2) 並べ替えます。今日は、さまざまなソート アルゴリズムの中で最も広く使用され、高速なソート アルゴリズムであるクイック ソート [平均時間計算量は O (n logn)] を紹介したいと思います。

ヒント１：「アルゴリズム」と「並べ替え」の基礎知識は、前回の「選択範囲の並べ替え方法」で詳しく説明していますので、記事末尾の該当記事リンクをクリックしてご覧ください。ここでは繰り返しません。

ヒント 2: 特に指定がない限り、この記事のクイック ソートは小さいものから大きいものの順に並べられています。

クイックソートの原理

クイックソートは分割交換ソートであり、通常分割統治法と呼ばれます。

分割統治法

基本的な考え方: 元の問題を、元の問題とサイズは小さいが構造が似ているいくつかのサブ問題に分解します。これらの部分問題を再帰的に解決し、これらの部分問題の結果を元の問題の結果に結合します。

基本原則

「基数」としてシーケンスから任意の数値を選択します。

「基数」より小さいすべての数値は「基数」以上のすべての数値に移動します。は「ベースライン」の右側の「」に移動されます。

この移動が終了すると、「ベースライン」は 2 つのシーケンスの中央になり、その後の並べ替えには参加しなくなります。

について繰り返します。 「ベースライン」の左右に 2 つのサブシーケンス すべてのサブシーケンスに 1 つの数値だけが残るまで、上記の手順が繰り返されます。

原理の図

既存のシーケンス [8、4、7、2、0、3、1] があり、以下はクイック ソート方法を使用して並べ替える方法を示します。

クイックソートを実装する手順の内訳

「ベンチマーク」を選択し、元の配列から分離します

まずベンチマークのインデックス値を取得し、次にスプライス配列メソッドを使用してベンチマーク値を取り出します。

ヒント: この例では、ベンチマークのインデックス値 = parseInt (シーケンス長 / 2)

ヒント: splice メソッドは元の配列を変更します。たとえば、 arr = [1, 2, 3]; ベースのインデックス値が 1、ベースの値が 2 の場合、元の配列は arr = [1, 3] になります

シーケンスを走査し、シーケンスを分割します

; 「ベースライン」サイズで 2 つのサブシーケンスに分割します

「ベースライン」より小さい数値は leftArr 配列に保存され、「ベースライン」以上の数値は rightArr 配列に保存されます

ヒント: もちろん、以下を入れることもできます。数値「ベンチマーク」は leftArr に格納され、「ベンチマーク」より大きい数値は rightArr に格納されます

シーケンスを走査してサイズを比較する必要があるため、各数値を「ベンチマーク」にするには、for ステートメントを使用して再帰呼び出しを実装し、サブシーケンスを走査し、サブシーケンスの結果を結合する必要があります

関数を定義し、仮パラメーターは配列を受け取るために使用されます

function QuickSort(arr) { };

1. サブシーケンスを走査するための再帰呼び出しを実装し、concat配列メソッドを使用しますサブシーケンスを結合した結果

サブシーケンスの長さを判断します

再帰呼び出しでは、サブシーケンスの長さが 1 に等しい場合、再帰呼び出しは停止し、現在の配列が返されます。

クイックソートメソッドの完全なコード

クイックソートメソッドの効率

時間の複雑さ

最悪の場合: 毎回選択される「ベースライン」は、シーケンス内の最小値/最大値です。状況はバブルソート法に似ており（一度に決定できるのは 1 つの数値 [基数] の順序のみです）、時間計算量は O(n^2) です

ベストケース: 毎回選択される「ベースライン」がシーケンス内の中央の数値 (位置の中央ではなく中央値です) の場合、現在のシーケンスは毎回同じ長さの 2 つのサブシーケンスに分割されます。このとき、1回目はn/2とn/2という2つの部分列があり、2回目はn/4、n/4、n/4、n/4というように4つの部分列があり、n個の数がかかります。ソートを完了するのに合計 logn 回かかります (2^x=n, x=logn)。計算量が n になるたびに、時間計算量は O(n logn) になります

空間計算量

最悪の場合: n -1 回の再帰呼び出しが必要で、空間複雑度は O(n) です

ベストケース: logn 回の再帰呼び出しが必要で、空間複雑度は O(logn) です

アルゴリズムの安定性

クイックソートは不安定なソートアルゴリズムです

例: 既存のシーケンスは[1, 0, 1, 3]で、「ベースライン」の数値が2番目の1として選択されます

最初のラウンドでは比較後は[0, 1, 1, 3]となり、左の列が[0]、右の列が[1, 3]になります(右の列の1は前の1です)

です見つけるのは難しくありません。元のシーケンスにある 2 つの 1 の順序が破壊され、順序が変更されます。これは当然、「不安定な」ソート アルゴリズムです

O について

前回の記事「バブルソート方法」では、 Oとは何か、ここでは多くは言いませんが、写真を見てください

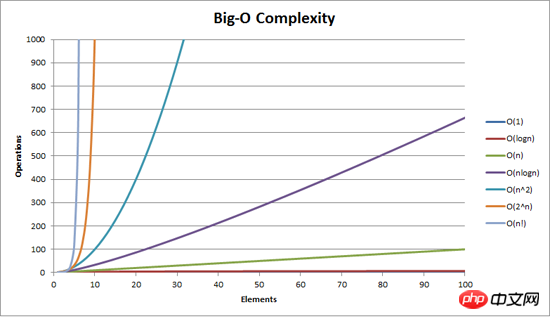
以上がクイックソートの実装方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。