ニューラルネットワークの理論的基礎とPythonの実装方法を詳しく解説-Python チュートリアル-php.cn

人工ニューラルネットワークは、動物のニューラルネットワークの行動特性を模倣し、分散並列情報処理を実行するアルゴリズム数学モデルです。この種のネットワークは、システムの複雑さに依存して、多数の内部ノード間の相互接続関係を調整することで情報処理の目的を達成し、自己学習して適応する能力を備えています。この記事では、ニューラルネットワークの理論的基礎と Python の実装について詳しく説明します。必要な方はぜひ参考にしてください。

1. 多層フォワードニューラルネットワーク

多層フォワードニューラルネットワークは、出力層、隠れ層、出力層の 3 つの部分で構成されます。各層は、入力層で構成されます。トレーニングセットで構成されます。インスタンス特徴ベクトルが渡され、接続ノードの重みを通じて次の層に渡されます。隠れ層の数は任意です。入力層は 1 つだけ、出力層は 1 つだけあります。

入力層を除くと、隠れ層と出力層の数の合計は n となり、ニューラルネットワークは n 層ニューラルネットワークと呼ばれます。次の図は、2 層のニューラルネットワークを示しています。理論的には、十分な隠れ層と十分な大きさのトレーニングセットがあれば、1 つの層で重み付けされた合計を変換し、出力します。

2. ニューラルネットワーク構造を設計します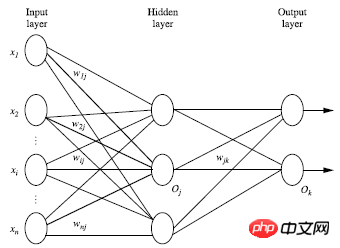

ニューラルネットワークを使用する前に、ニューラルネットワークの層数と各層のユニット数を決定する必要があります学習プロセスを高速化するには、通常、特徴ベクトルを入力層に渡す前に 0 から 1 の間に標準化する必要があります。

離散型変数は、固有値に対応する各入力ユニットに割り当てられる可能な値にエンコードできます。

例: 固有値 A は 3 つの値 (a0、a1、a2) を持つ可能性があり、3 つの入力単位を使用して A を表すことができます

A=a0 の場合、a0 を表す単位値は 1 で、残りはは 0;

A=a1 の場合、a1 を表すユニット値は 1、残りは 0; A=a2 の場合、a2 を表すユニット値は 0 1、残りは 0 です

ネットワークは分類問題と回帰問題の両方を解決できます。分類問題の場合、2 つのカテゴリがある場合、1 つの出力ユニット (0 と 1) を使用して 2 つのカテゴリをそれぞれ表すことができます。3 つ以上のカテゴリがある場合、各カテゴリは 1 つの出力ユニットで表されるため、ユニットの数は出力層のは、通常、1 つのカテゴリの数量に等しくなります。

最適な隠れ層の数を設計するための明確なルールはありません。通常、実験は実験的なテストのエラーと精度に基づいて改善されます。

3. 相互検証方法

精度を計算するには?最も簡単な方法は、トレーニングセットとテストセットのセットを使用してモデルを取得し、テスト結果をモデルに入力します。精度を得るためにテストセットを使用します。

機械学習の分野で一般的に使用される手法は、相互検証手法です。データのセットは 2 つの部分に分割されませんが、10 つの部分に分割される場合があります。 1 回目: 1 番目の部分はテストセットとして使用され、残りの 9 つの部分はトレーニングセットとして使用されます。時間: 2 番目の部分はテストセットとして使用され、残りの 9 つの部分はトレーニングセットとして使用されます。トレーニングセット; 10 回のトレーニング後、10 セットの精度が得られます。 10セットのデータが得られます。ここで 10 は特殊なケースです。一般に、データは k 個の部分に分割され、そのアルゴリズムは K 分割クロス検証と呼ばれます。つまり、k 個の部分のうちの 1 つが毎回テストセットとして選択され、残りの k-1 個の部分がテストセットとして使用されます。トレーニングセットを k 回繰り返して最終的に平均精度を取得するのは、より科学的で正確な方法です。

4. BP アルゴリズム

反復を通じてトレーニングセット内のインスタンスを処理します。

ニューラルネットワークを通過した後の予測値と真の値の差を比較します。

逆方向 (出力層 = > 隠れ層 => 入力層から) エラーを最小限に抑え、各接続の重みを更新します

4.1. アルゴリズムの詳細な紹介 入力: データセット、学習率、多層ニューラルネットワークアーキテクチャ; 出力: トレーニングされたニューラルネットワーク;

初期化の重みとバイアス: -1 から 1 (またはその他) の間でランダムに初期化され、各ユニットはトレーニングインスタンス X ごとに次の手順を実行します。 1、入力層から順方向に送信:

ニューラルネットワークの模式図と組み合わせた解析:

入力層から隠れ層へ:

隠れ層から出力層へ:

2 つの式を要約すると、次のようになります:

Ij は現在のレイヤーの単位値、Oi は前のレイヤーの単位値、wij は 2 つのレイヤー間の重み値であり、 2 つの単位値、sitaj は各層のバイアス値です。各層の出力に対して非線形変換を実行する必要があります。概略図は次のとおりです。

現在の層の出力は Ij で、f は活性化関数とも呼ばれる非線形変換関数です。は次のように定義されます:

つまり、各層の出力は次のようになります:

このようにして、順方向の入力値を通じて各層の出力値を取得できます。

2. 誤差に基づく逆方向送信出力層の場合: Tk は真の値、Ok は予測値

隠れ層の場合:

ここで l は学習率

偏った更新:

3. 終了条件

予測されたエラー率が特定の閾値を下回る。

事前に設定された一定のサイクル数に達する。

4. 非線形変換関数

上記の非線形変換関数 f は、一般に 2 つの関数を使用できます:

(1) Tanh(x) 関数:

tanh(x)=sinh(x)/cosh(x)

sinh(x)=(exp(x)-exp(-x))/2

cosh(x)=(exp(x)+exp(-x))/2

(2) 上で使用した論理関数この記事は論理関数

5. BP ニューラルネットワークの Python 実装は、非線形変換関数を定義するために最初に numpy モジュール

import numpy as np

ログイン後にコピー

をインポートする必要があります。関数も使用する必要があるため、オブジェクト指向を使用して、主にどの非線形関数を選択するかを使用して、BP ニューラルネットワークの形式 (層数、各層のユニット数) を設計するための

def tanh(x):
  return np.tanh(x)
def tanh_deriv(x):
  return 1.0 - np.tanh(x)*np.tanh(x)
def logistic(x):
  return 1/(1 + np.exp(-x))
def logistic_derivative(x):
  return logistic(x)*(1-logistic(x))

ログイン後にコピー

を一緒に定義します、重みを初期化します。 Layers は、各レイヤーのユニット数を含むリストです。

class NeuralNetwork:
  def __init__(self, layers, activation=&#39;tanh&#39;):
    """
    :param layers: A list containing the number of units in each layer.
    Should be at least two values
    :param activation: The activation function to be used. Can be
    "logistic" or "tanh"
    """
    if activation == &#39;logistic&#39;:
      self.activation = logistic
      self.activation_deriv = logistic_derivative
    elif activation == &#39;tanh&#39;:
      self.activation = tanh
      self.activation_deriv = tanh_deriv
 
    self.weights = []
    for i in range(1, len(layers) - 1):
      self.weights.append((2*np.random.random((layers[i - 1] + 1, layers[i] + 1))-1)*0.25)
      self.weights.append((2*np.random.random((layers[i] + 1, layers[i + 1]))-1)*0.25)

ログイン後にコピー

アルゴリズムを実装する

  def fit(self, X, y, learning_rate=0.2, epochs=10000):
    X = np.atleast_2d(X)
    temp = np.ones([X.shape[0], X.shape[1]+1])
    temp[:, 0:-1] = X
    X = temp
    y = np.array(y)
 
    for k in range(epochs):
      i = np.random.randint(X.shape[0])
      a = [X[i]]
 
      for l in range(len(self.weights)):
        a.append(self.activation(np.dot(a[l], self.weights[l])))
      error = y[i] - a[-1]
      deltas = [error * self.activation_deriv(a[-1])]
 
      for l in range(len(a) - 2, 0, -1):
        deltas.append(deltas[-1].dot(self.weights[l].T)*self.activation_deriv(a[l]))
      deltas.reverse()
 
      for i in range(len(self.weights)):
        layer = np.atleast_2d(a[i])
        delta = np.atleast_2d(deltas[i])
        self.weights[i] += learning_rate * layer.T.dot(delta)

ログイン後にコピー

予測を実装する

  def predict(self, x):
    x = np.array(x)
    temp = np.ones(x.shape[0]+1)
    temp[0:-1] = x
    a = temp
    for l in range(0, len(self.weights)):
      a = self.activation(np.dot(a, self.weights[l]))
    return a

ログイン後にコピー

予測用の数値のセットを与え、上記のプログラムファイルはBP

という名前で保存されます

りー

結果は次のとおりです:

from BP import NeuralNetwork
import numpy as np
 
nn = NeuralNetwork([2,2,1], &#39;tanh&#39;)
x = np.array([[0,0], [0,1], [1,0], [1,1]])
y = np.array([1,0,0,1])
nn.fit(x,y,0.1,10000)
for i in [[0,0], [0,1], [1,0], [1,1]]:
  print(i, nn.predict(i))

ログイン後にコピー