キャンバスを使用して曲線を描くアニメーションの例

フロントエンド開発ではベジェ曲線が随所に登場しますが、この記事では主にキャンバスを使用して曲線アニメーションを描画する例を紹介します。

• SVG と Canvas では、提供される曲線はベジェ曲線をネイティブに使用するために使用できます

• イージング アルゴリズムを記述し、css transition-timing- を設定するためにも使用できます。 function プロパティを使用すると、ベジェ曲線を使用してトランジションのイージング計算を記述することができますtransition-timing-function属性，可以使用贝塞尔曲线来描述过渡的缓动计算

• 几乎所有前端2D或3D图形图表库(echarts，d3，three.js)都会使用到贝塞尔曲线

这篇文章我准备从实现一个非常简单的曲线动画效果入手，帮助大家彻底地弄懂什么是贝塞尔曲线，以及它有哪些特性，文章中有一点点数学公式，但是都非常简单:)。

实现这样一个曲线动画

可以点击这里查看在线演示

在写代码之前，先了解一下什么是贝塞尔曲线吧。

贝塞尔曲线

贝塞尔曲线（Bezier curve）是计算机图形学中相当重要的参数曲线，它通过一个方程来描述一条曲线，根据方程的最高阶数，又分为线性贝赛尔曲线，二次贝塞尔曲线、三次贝塞尔曲线和更高阶的贝塞尔曲线。

下面详细介绍一下用得比较多的二次贝塞尔曲线和三次贝塞尔曲线

二次贝塞尔曲线

二次贝塞尔曲线由三个点P0,P1,P2来确定，这些点也被称作控制点。曲线的方程为：

这个方程其实有它的几何意义，它表示可以通过这样的步骤来绘制一条曲线：

• 选定一个0-1的t值

• 通过P0和P1计算出点Q0，Q0在P0 P1连成的直线上，并且length( P0, Q0 ) = length( P0, P1 ) * t

• 同样，通过P1和P2计算出Q1，使得length( P1, Q1 ) = length( P1, P2 ) * t

• 再重复一次这个步骤，通过Q1和Q2计算出B，使得length( Q0, Q1 ) = length( Q0, B ) * t。B就为当前曲线上的点

注：上面的length表示两点之间的长度

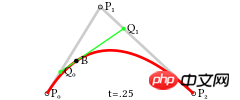
图：二次贝塞尔曲线结构

有了曲线方程，我们直接代入具体的t值就能算出点B了。

如果将t的值从0过渡到1，不断计算点B，就可以得到一条二次贝塞尔曲线：

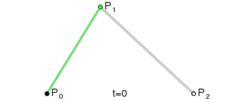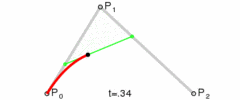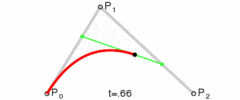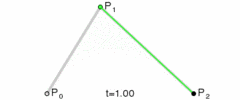
图：二次贝塞尔线绘制过程

在canvas中，绘制二次贝塞尔曲线的方法为

ctx.quadraticCurveTo( p1x, p1y, p2x, p2y )

其中p1x, p1y, p2x, p2y为后两个控制点（P1和P2）的横纵坐标，它默认将当前路径的起点作为一个控制点（P0）。

三次贝塞尔曲线

三次贝塞尔曲线需要四个点P0,P1,P2,P3来确定，曲线方程为

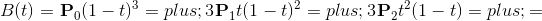
它的计算过程和二次贝塞尔曲线类似，这里不再赘述，可以看下图：

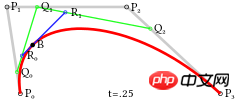
图：三次贝塞尔曲线结构

同样，将t的值从0过渡到1，就可以绘制出一条三次贝塞尔曲线：

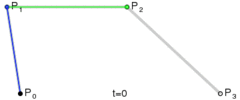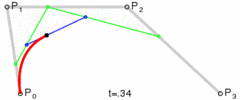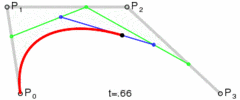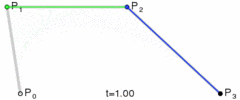
图：三次贝塞尔曲线绘制过程

在canvas中，绘制三次贝塞尔曲线的方法为

ctx.bezierCurveTo( p1x, p1y, p2x, p2y, p3x, p3y )

其中p1x, p1y, p2x, p2y, p3x, p3y为后三个控制点（P1,P2和P3）的横纵坐标，它默认将当前路径的起点作为一个控制点（P0

ほぼすべてのフロントエンド 2D または 3D グラフィック チャート ライブラリ (echarts、d3、three.js) でこれが使用されます。曲線

🎜 この記事では、ベジェ曲線とは何か、そしてその特性を誰もが完全に理解できるように、非常に単純な曲線アニメーション効果を実装することから始めます。この記事には少し数学が含まれています。しかし、それはすべて非常に簡単です:)。 🎜🎜🎜このような曲線を実現しますアニメーション🎜🎜ここをクリックしてオンラインデモをご覧ください🎜🎜 コードを書く前に、まずベジェ曲線とは何かを理解しましょう。 🎜

ベジェ曲線

🎜 ベジェ曲線は、コンピュータ グラフィックスにおいて非常に重要なパラメトリック曲線です。方程式の最上位に従って、次のように分割されます。二次ベジェ曲線、三次ベジェ曲線、高次ベジェ曲線。 🎜🎜以下は、より一般的に使用される二次ベジェ曲線と三次ベジェ曲線について詳しく説明します🎜🎜二次ベジェ曲線🎜🎜二次ベジェ曲線は、3 つの点 P0、P1 で構成されますcode>、<code>P2 を決定するため、これらのポイントはコントロール ポイントとも呼ばれます。曲線の方程式は次のとおりです: 🎜🎜 🎜🎜🎜この方程式には実際には幾何学的な意味があります。これは、次の手順に従って曲線を描くことができることを意味します: 🎜🎜🎜🎜0-1の t を選択します。 > 値 🎜🎜🎜🎜 は、P0 と P1 から Q0 を指すように計算されます。Q0 は にあります>P0 code> P1 は直線上にあり、 length( P0, Q0 ) = length( P0, P1 ) * t🎜🎜🎜🎜 同様に、P1 および P2 を通じて、 length( P1, Q1 ) = length( P1, P2 ) * t となるように <code>Q1 を計算します。 code>🎜🎜🎜 🎜この手順をもう一度繰り返して、B から Q1 および Q2 までを計算します。これにより、length( Q0, Q1) = 長さ( Q0 , B ) * t。 B は現在のカーブ上の点です🎜🎜🎜注: 上記の length は 2 つの点間の長さを表します🎜🎜🎜🎜写真: 二次ベジェ曲線の構造🎜🎜 はい曲線方程式では、特定の t 値を直接代入することで点 B を計算できます。 🎜🎜t の値を 0 から 1 に遷移させ、点 B を継続的に計算すると、次のようになります。二次ベジェ曲線: 🎜🎜 🎜🎜写真: 二次ベジェ線描画プロセス🎜🎜キャンバスでの二次ベジェ曲線の描画方法は🎜

/**
 * 绘制二次贝赛尔曲线路径
 * @param  {Object} ctx
 * @param  {Array<number>} p0
 * @param  {Array<number>} p1
 * @param  {Array<number>} p2
 */
function drawCurvePath( ctx, p0, p1, p2 ) {
    // ...
}

🎜ここで、p1x, p1y, p2x, p2y が最後です。 2 つの制御点 (P1 と P2)。デフォルトでは、現在のパスの開始点が制御点 (P0) になります。 🎜🎜3 次ベジェ曲線🎜🎜 3 次ベジェ曲線には、4 つの点 P0、P1、P2、P3 が必要です。決定すると、曲線方程式は 🎜🎜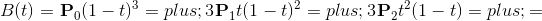🎜🎜🎜計算プロセスは 2 次ベジェ曲線に似ています。ここでは詳しく説明しません。以下の図を参照してください: 🎜🎜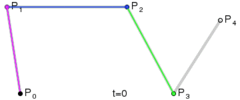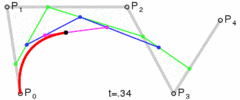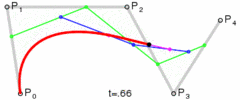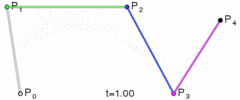🎜🎜図:3次ベジェ曲線の構造🎜🎜同様に、tの値を変更します。 0 から 1 に移行すると、3 次ベジェ曲線を描くことができます: 🎜🎜🎜🎜図: 3次ベジェ曲線描画プロセス🎜🎜キャンバスで3次ベジェ曲線を描画しますメソッドは 🎜

/**
 * 绘制二次贝赛尔曲线路径
 * @param  {CanvasRenderingContext2D} ctx
 * @param  {Array<number>} p0
 * @param  {Array<number>} p1
 * @param  {Array<number>} p2
 */
function drawCurvePath( ctx, p0, p1, p2 ) {
    ctx.moveTo( p0[ 0 ], p0[ 1 ] );
    ctx.quadraticCurveTo( 
        p1[ 0 ], p1[ 1 ],
        p2[ 0 ], p2[ 1 ]
    );
}

🎜where p1x、p1y、p2x、p2y、p3x、p3y は最後の 3 つのコントロール ポイント (P1、P2、および P3) です。 )、デフォルトでは、現在のパスの開始点が制御点 (P0) になります。 🎜🎜ベジェ曲線の特徴🎜🎜3次ベジェ曲線の背後には高次のベジェ曲線があり、その描画プロセスもより複雑です🎜

四次贝塞尔曲线

图：四次贝塞尔曲线

五次贝塞尔曲线

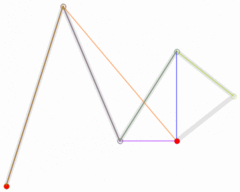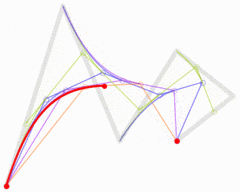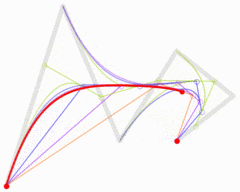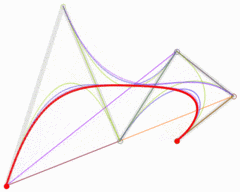图：五次贝塞尔曲线

我们可以归纳出贝塞尔曲线有几个重要的特征：

1. n阶贝塞尔曲线需要n+1个点来确定

2. 贝塞尔曲线是平滑的

3. 贝塞尔曲线的起点和终点与对应控制点的连线相切

绘制贝塞尔曲线

复习完基础概念，接下来就要讲如果绘制贝塞尔曲线啦

为简单起见，我们选择使用二次贝塞尔曲线。

我们先不考虑动画的事，我们先将问题简化成：给定一个起点和一个终点，需要实现一个函数，它能够绘制出一条曲线。

也就是说我们需要实现一个函数drawCurvePath，除渲染上下文ctx外（不清楚ctx是什么的同学可以先熟悉下canvas的基本概念），它接受三个参数，分别为二次贝塞尔曲线的三个控制点。我们将样式控制移到函数外，drawCurvePath只用来绘制路径。

/**
 * 绘制二次贝赛尔曲线路径
 * @param  {Object} ctx
 * @param  {Array<number>} p0
 * @param  {Array<number>} p1
 * @param  {Array<number>} p2
 */
function drawCurvePath( ctx, p0, p1, p2 ) {
    // ...
}

前文提到过，在canvas中，绘制二次贝赛尔曲线的方法是quadraticCurveTo，所以只要短短两行就能完成这个方法。

/**
 * 绘制二次贝赛尔曲线路径
 * @param  {CanvasRenderingContext2D} ctx
 * @param  {Array<number>} p0
 * @param  {Array<number>} p1
 * @param  {Array<number>} p2
 */
function drawCurvePath( ctx, p0, p1, p2 ) {
    ctx.moveTo( p0[ 0 ], p0[ 1 ] );
    ctx.quadraticCurveTo( 
        p1[ 0 ], p1[ 1 ],
        p2[ 0 ], p2[ 1 ]
    );
}

这样就完成了基本的绘制二次贝塞尔曲线的方法了。

但是函数这样设计有点小问题

如果我们是在做一个图形库，我们想给使用者提供一个绘制曲线的方法。

对于使用者来说，他只想在给定的起点和终点间间绘制一条曲线，他想要得到的曲线尽量美观，但是又不想关心具体的实现细节，如果还需要给第三个点，使用者会有一定的学习成本（至少需要弄明白什么是贝塞尔曲线）。

看到这里你可能会比较疑惑，即使是二次贝塞尔曲线也需要三个控制点，只有起点和终点怎么绘制曲线呢。

我们可以在起点和终点的垂直平分线上选一点作为第三个控制点，可以提供给使用者一个参数来控制曲线的弯曲程度，现在函数就变成了这样

/**
 * 绘制一条曲线路径
 * @param  {CanvasRenderingContext2D} ctx
 * @param  {Array<number>} start 起点
 * @param  {Array<number>} end 终点
 * @param  {number} curveness 曲度(0-1)
 */
function drawCurvePath( ctx, start, end, curveness ) {
    // ...
}

我们用curveness来表示曲线的弯曲程度，也就是第三个控制点的偏离程度。这样很容易就能计算出中间点。
现在完整的函数变成了这样：

/**
 * 绘制一条曲线路径
 * @param  {Object} ctx canvas渲染上下文
 * @param  {Array<number>} start 起点
 * @param  {Array<number>} end 终点
 * @param  {number} curveness 曲度(0-1)
 */
function drawCurvePath( ctx, start, end, curveness ) {
    // 计算中间控制点
    var cp = [
         ( start[ 0 ] + end[ 0 ] ) / 2 - ( start[ 1 ] - end[ 1 ] ) * curveness,
         ( start[ 1 ] + end[ 1 ] ) / 2 - ( end[ 0 ] - start[ 0 ] ) * curveness
    ];
    ctx.moveTo( start[ 0 ], start[ 1 ] );
    ctx.quadraticCurveTo( 
        cp[ 0 ], cp[ 1 ],
        end[ 0 ], end[ 1 ]
    );
}

对，就这么短短几行，接下来我们就可以通过它来绘制一条曲线了，代码如下

<!DOCTYPE html>
<html lang="en">
    <head>
        <title>draw curve</title>
    </head>
    <body>
        <canvas id="canvas" width="800" height="800"></canvas>
        <script>
            var canvas = document.getElementById( 'canvas' );
            var ctx = canvas.getContext( '2d' );
            
            ctx.lineWidth = 2;
            ctx.strokeStyle = '#000';
            ctx.beginPath();
    
            drawCurvePath( 
                ctx,
                [ 100, 100 ],
                [ 200, 300 ],
                0.4
            );
            
            ctx.stroke();
            
            function drawCurvePath( ctx, start, end, curveness ) {
                // ...
            }
        </script>
    </body>
</html>

绘制结果：

绘制一条曲线

绘制贝塞尔曲线动画

终于来到文章的本体啦，我们的目的不是绘制一条静态的曲线，我们想绘制一条有过渡效果的曲线。

简化一下问题，那就是我们希望绘制曲线的函数还接受另一个参数，表示绘制曲线的百分比。我们定时去调用这个函数，递增百分比这个参数，就能画出动画了。

我们新增一个参数percent来表示百分比，现在函数变成了这样：

/**
 * 绘制一条曲线路径
 * @param  {Object} ctx canvas渲染上下文
 * @param  {Array<number>} start 起点
 * @param  {Array<number>} end 终点
 * @param  {number} curveness 曲度(0-1)
 * @param  {number} percent 绘制百分比(0-100)
 */
function drawCurvePath( ctx, start, end, curveness, percent ) {
    // ...
}

但是canvas提供的quadraticCurveTo方法只能绘制一条完整的二次贝赛尔曲线，没有办法去控制它只画一部分。

画完后用clearRect擦除掉一部分？这不太可行，因为很难确定要擦除的范围。如果曲线的线宽比较宽，就还需要保证擦除的边界和曲线末端垂直，问题就变得很复杂了。

现在再重新看看这张图

我们是不是可以将percent这个参数理解成t值，然后通过贝赛尔曲线方程去计算出中间所有的点，用直线连接起来，以此模拟绘制贝赛尔曲线的一部分呢？

方法一

我们不再用canvas提供的quadraticCurveTo来绘制曲线，而是通过贝赛尔曲线的方程计算出一系列点，用多端直线来模拟曲线。

这样做的好处时，我们可以很容易的控制绘制的范围。

那么函数实现就变成了这样：

/**
 * 绘制一条曲线路径
 * @param  {Object} ctx canvas渲染上下文
 * @param  {Array<number>} start 起点
 * @param  {Array<number>} end 终点
 * @param  {number} curveness 曲度(0-1)
 * @param  {number} percent 绘制百分比(0-100)
 */
function drawCurvePath( ctx, start, end, curveness, percent ) {

    var cp = [
         ( start[ 0 ] + end[ 0 ] ) / 2 - ( start[ 1 ] - end[ 1 ] ) * curveness,
         ( start[ 1 ] + end[ 1 ] ) / 2 - ( end[ 0 ] - start[ 0 ] ) * curveness
    ];
    
    ctx.moveTo( start[ 0 ], start[ 1 ] );
    
    for ( var t = 0; t <= percent / 100; t += 0.01 ) {

        var x = quadraticBezier( start[ 0 ], cp[ 0 ], end[ 0 ], t );
        var y = quadraticBezier( start[ 1 ], cp[ 1 ], end[ 1 ], t );
        
        ctx.lineTo( x, y );
    }
    
}

function quadraticBezier( p0, p1, p2, t ) {
    var k = 1 - t;
    return k * k * p0 + 2 * ( 1 - t ) * t * p1 + t * t * p2;    // 这个方程就是二次贝赛尔曲线方程
}

接下来就可以通过设置定时器，每隔一段时间调用一次这个方法，并且递增percent

为了动画更加平滑，我们使用requestAnimationFrame来代替定时器

<!DOCTYPE html>
<html lang="en">
    <head>
        <title>draw curve</title>
    </head>
    <body>
        <canvas id="canvas" width="800" height="800"></canvas>
        <script>
            var canvas = document.getElementById( 'canvas' );
            var ctx = canvas.getContext( '2d' );
            
            ctx.lineWidth = 2;
            ctx.strokeStyle = '#000';
            
            var percent = 0;
            
            function animate() {
                
                ctx.clearRect( 0, 0, 800, 800 );
                ctx.beginPath();

                drawCurvePath( 
                    ctx,
                    [ 100, 100 ],
                    [ 200, 300 ],
                    0.2,
                    percent
                );
    
                ctx.stroke();
    
                percent = ( percent + 1 ) % 100;
                
                requestAnimationFrame( animate );
                
            }
            
            animate();
            
            function drawCurvePath( ctx, start, end, curveness, percent ) {
                // ...
            }
        </script>
    </body>
</html>

得到的结果：

这样基本实现了我们的需求，但它有一个问题：

测试发现，进行一次lineTo的时间和一次quadraticCurveTo的时间差不多，但是quadraticCurveTo只需要一次就能画出曲线，而使用lineTo则需要数十次。

换言之，用这样的方式绘制曲线，和我们前面的实现方式相比性能下降了数十倍之多。在绘制一条曲线时可能感觉不到区别，但是如果需要同时绘制上千条曲线，性能就会受到很大的影响。

方法二

那有没有什么方法可以做到用quadraticCurveTo来实现绘制完整曲线的一部分呢？

我们再次回到这张图

在中间的某一时刻，例如t=0.25时，它是这样的：

我们注意到，曲线P0-B这一段似乎也是贝赛尔曲线，它的控制点变成了P0，Q0，B。

现在问题就迎刃而解了，我们只需要每次计算出Q0，B，就能得到其中一小段贝赛尔曲线的控制点，然后就可以通过quadraticCurveTo来绘制它了。

代码如下：

/**
 * 绘制一条曲线路径
 * @param  {Object} ctx canvas渲染上下文
 * @param  {Array<number>} start 起点
 * @param  {Array<number>} end 终点
 * @param  {number} curveness 曲度(0-1)
 * @param  {number} percent 绘制百分比(0-100)
 */
function drawCurvePath( ctx, start, end, curveness, percent ) {

    var cp = [
         ( start[ 0 ] + end[ 0 ] ) / 2 - ( start[ 1 ] - end[ 1 ] ) * curveness,
         ( start[ 1 ] + end[ 1 ] ) / 2 - ( end[ 0 ] - start[ 0 ] ) * curveness
    ];
    
    var t = percent / 100;
    
    var p0 = start;
    var p1 = cp;
    var p2 = end;
    
    var v01 = [ p1[ 0 ] - p0[ 0 ], p1[ 1 ] - p0[ 1 ] ];     // 向量<p0, p1>
    var v12 = [ p2[ 0 ] - p1[ 0 ], p2[ 1 ] - p1[ 1 ] ];     // 向量<p1, p2>

    var q0 = [ p0[ 0 ] + v01[ 0 ] * t, p0[ 1 ] + v01[ 1 ] * t ];
    var q1 = [ p1[ 0 ] + v12[ 0 ] * t, p1[ 1 ] + v12[ 1 ] * t ];
    
    var v = [ q1[ 0 ] - q0[ 0 ], q1[ 1 ] - q0[ 1 ] ];       // 向量<q0, q1>

    var b = [ q0[ 0 ] + v[ 0 ] * t, q0[ 1 ] + v[ 1 ] * t ];
    
    ctx.moveTo( p0[ 0 ], p0[ 1 ] );

    ctx.quadraticCurveTo( 
        q0[ 0 ], q0[ 1 ],
        b[ 0 ], b[ 1 ]
    );

}

将前面写的页面替换成上面的代码，可以看到得到的结果是一样的：

绘制动画

现在已经解决了最关键的问题，我们可以绘制动画啦。
不过这一部分并不重要，我就不贴代码了。

完整代码可以看这里

相关推荐：

Python之正弦曲线实现方法分析

使用CSS做贝塞尔曲线

css动画之模拟正余弦曲线的实例分享

以上がキャンバスを使用して曲線を描くアニメーションの例の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。