PHP はいくつかの一般的な並べ替えアルゴリズムを実装しています
交換ソート: 交換ソートの基本的な考え方は、2 つのレコードのキー値を比較し、2 つのレコードのキー値が逆の順序である場合、小さい方のレコードになるように 2 つのレコードを交換することです。キー値がシーケンス内で前方に移動されます。キー値が大きいレコードはシーケンスの後方に移動されます。 1. バブルソート
バブルソート(バブルソート、台湾語訳:バブルソートまたはバブルソート)は、シンプルな
ソートアルゴリズム
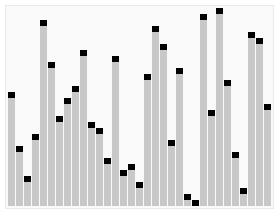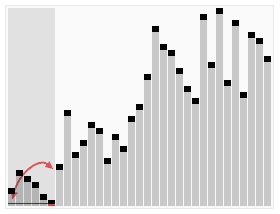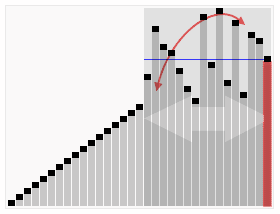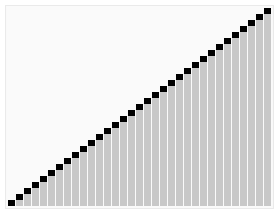
です。ソート対象のシーケンスを繰り返し調べて、一度に 2 つの要素を比較し、順序が間違っている場合はそれらを交換します。配列を訪問する作業は、それ以上の交換が必要なくなるまで繰り返されます。これは、配列がソートされたことを意味します。このアルゴリズムの名前は、小さい要素がスワッピングによって配列の先頭にゆっくりと「浮動」するという事実に由来しています。 
隣接する要素を比較します。最初のものが 2 番目のものより大きい場合は、両方を交換します。
隣接する要素の各ペアに対して同じことを行い、最初の最初のペアから始めて、最後の最後のペアで終了します。この時点では、最後の要素が最大の数値である必要があります。
最後の要素を除くすべての要素に対して上記の手順を繰り返します。
比較する数値のペアがなくなるまで、要素の数を減らしながら上記の手順を繰り返します。
- バブルソートは最も理解しやすいですが、時間計算量 (O(n^2)) も最も大きいものの 1 つです。実装コードは次のとおりです。
<br/>
ログイン後にコピーログイン後にコピーログイン後にコピー$arr=array(1,43,54,62,21,66,32,78,36,76,39); 関数
getpao(- $arr)
) {
$len
=- count
($arr); //空の値を設定します(
$i - =1;
$i<$len
; - $i
++) //このレイヤーはループに使用され、数値に必要な回数を制御します各ラウンドで比較します
for($k=0;$k<$len-$i; $k++)
{
if($arr[$k]> $arr[$k+1] )
{
$tmp=$arr[] $k+1];
$arr[$k+1]=$arr[$k];
}}}}rturn$arr; 2. クイックソート
- はじめに:
クイックソートは、
Tony Hall によって開発された並べ替えアルゴリズム によって開発されました。平均すると、 - n
項目の並べ替えにはΟ(
n log - n
)の比較が必要です。最悪の場合、Ο(
n - 2
) の比較が必要になりますが、この状況は一般的ではありません。実際、クイック ソートは、ほとんどのアーキテクチャで内部ループを効率的に実装でき、ほとんどの実世界のデータでは 2 次項の可能性が高いため、他の Ο(n log n) アルゴリズムよりも大幅に高速であることがよくあります。必要な時間を短縮する設計の選択を決定します。 手順:
シーケンスから「ピボット」と呼ばれる要素を選択します。
シーケンスを並べ替えます。ピボット値より小さいすべての要素はピボットの前に配置され、ピボットより大きいすべての要素が配置されます。値はベースの後ろに配置されます (同じ数値をどちらの側にも置くことができます)。このパーティションが終了すると、塩基はシーケンスの途中になります。これは、パーティション操作と呼ばれます。
基本値より小さい要素の部分配列と基本値より大きい要素の部分配列を再帰的に並べ替えます。
クイックソートも効率的なソートアルゴリズムであり、その時間計算量もO(nlogn)です。コードは以下のとおりです。
$ 長さ
- =
数 ($arr);
- 1) {
//リターンがない場合は、配列内の要素の数が 1 より大きいため、並べ替える必要があることを意味します
// ルーラーを選択します //最初の要素を選択します
$base_num = $arr
[0]; //トラバースルーラーを除くすべての要素をサイズに応じて 2 つの配列に入れます
//初期 2 つの配列を変換します
$left_array = 配列
();//、それは定規
-
$right_array = array( );//それは定規より大きいです
if($base_num > $arr[$i]) {それを左の配列に入れます
else { そうです
/左と右のアレイで同じソートを実行しますright_array = Quick_sort($right_array); //左のルーラーを右のルーラーとマージします
return array_merge($left_array, array($base_num), $right_array); }
選択ソート
選択ソートには、直接選択ソートとヒープソートの 2 つのタイプがあります。 i+1 ( i=1,2,3,...,n-1) レコード、順序付けされたシーケンスの i 番目のレコードとして最小のキー値を持つレコードを選択します
3. 選択ソート 概要:
選択並べ替えは、シンプルで直感的な
並べ替えアルゴリズムです。仕組みは次のとおりです。まず、ソートされていないシーケンスの中で最小の要素を見つけて、それをソートされたシーケンスの先頭に格納します。次に、引き続きソートされていない残りの要素から最小の要素を見つけて、それをソートされたシーケンスの最後に置きます。すべての要素がソートされるまで続きます。
選択の並べ替えも比較的簡単に理解でき、時間計算量も O(n^2) です。実装コードは次のとおりです:
<br/>
ログイン後にコピーログイン後にコピーログイン後にコピー
view plain <br/>
<br/>コピー
function select_sort($arr) {
//実装アイデア 二重ループが完了し、外側の制御ラウンド番号、現在の最小値。内部層によって制御される比較の数
//$i 現在の最小値の位置、比較に参加する必要がある要素
for ($i =0, $len=count($arr); $i<$レン-1 ; $i ++ ) {
$i; /$j は現在 $i 以降の要素と比較する必要があります。
$j++) { // $arr[$p] ($arr[$p ] >
// 既知の最小値を比較に使用する必要があります。
//現在の最小値の位置が決定され、$p に保存されました。
//最小値の位置が現在仮定されている位置 $i と異なることが判明した場合、位置を入れ替えることができます
if ($ p != $i) {
$p]; [$p] = $arr[$i
]; [$i] = $tmp;
//最終結果を返す
return $arr; }
4. ヒープソート
はじめに: <br/>
スタッキングソート (ヒープソート) は、
ヒープのデータ構造を使用して設計されたソートアルゴリズムを指します。ヒープは、完全なバイナリツリーを近似し、同時にヒーププロパティを満たす構造です。つまり、子ノードのキー値またはインデックスは常に小さくなります(または大きくなります)。 ) 親ノードよりも。 手順:
ヒープソートとは、配列の特性を使用して、指定されたインデックスにある要素を迅速に見つけるために、積み重ねられたツリー (ヒープ) などのデータ構造を使用して設計されたソートアルゴリズムを指します。ヒープは、大きなルート ヒープと小さなルート ヒープに分割され、完全なバイナリ ツリーになります。大規模なルート ヒープの要件は、各ノードの値がその親ノードの値以下であること、つまり A[PARENT[i]] >= A[i] であることです。配列の非降順ソートでは、大きなルート ヒープの要件に従って、最大値がヒープの先頭になければならないため、大きなルート ヒープを使用する必要があります。
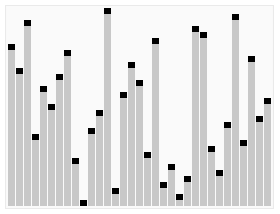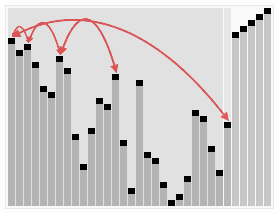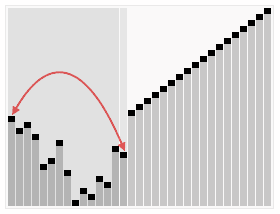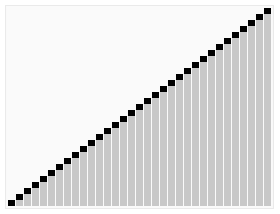
並べ替え効果:

 <br/>
<br/>堆排序是一种高效的排序算法,它的时间复杂度是O(nlogn)。原理是:先把数组转为一个最大堆,然后把第一个元素跟第i元素交换,然后把剩下的i-1个元素转为最大堆,然后再把第一个元素与第i-1个元素交换,以此类推。实现代码如下:
function heapSort($arr) { $len = count($arr); // 先建立最大堆 for ($i = floor(($len - 1) / 2); $i >= 0; $i--) { $s = $i; $childIndex = $s * 2 + 1; while ($childIndex < $len) { // 在父、左子、右子中 ,找到最大的 if ($childIndex + 1 < $len && $arr[$childIndex] < $arr[$childIndex + 1]) $childIndex++; if ($arr[$s] < $arr[$childIndex]) { $t = $arr[$s]; $arr[$s] = $arr[$childIndex]; $arr[$childIndex] = $t; $s = $childIndex; $childIndex = $childIndex * 2 + 1; } else { break; } } } // 从最后一个元素开始调整 for ($i = $len - 1; $i > 0; $i--) { $t = $arr[$i]; $arr[$i] = $arr[0]; $arr[0] = $t; // 调整第一个元素 $s = 0; $childIndex = 1; while ($childIndex < $i) { // 在父、左子、右子中 ,找到最大的 if ($childIndex + 1 < $i && $arr[$childIndex] < $arr[$childIndex + 1]) $childIndex++; if ($arr[$s] < $arr[$childIndex]) { $t = $arr[$s]; $arr[$s] = $arr[$childIndex]; $arr[$childIndex] = $t; $s = $childIndex; $childIndex = $childIndex * 2 + 1; } else { break; } } } return $arr; }$arr = [3,1,13,5,7,11,2,4,14,9,15,6,12,10,8]; print_r(bubbleSort($arr));ログイン後にコピー<br/>
<br/>
插入排序
五、插入排序
介绍:
插入排序(Insertion Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
步骤:
从第一个元素开始,该元素可以认为已经被排序
取出下一个元素,在已经排序的元素序列中从后向前扫描
如果该元素(已排序)大于新元素,将该元素移到下一位置
重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
将新元素插入到该位置中
重复步骤2
 <br/>感觉插入排序跟冒泡排序有点相似,时间复杂度也是O(n^2),实现代码如下:
<br/>感觉插入排序跟冒泡排序有点相似,时间复杂度也是O(n^2),实现代码如下:[php]プレーンに表示copy
<br/>
function insert_sort($arr) {
//どの部分にするか区別します 並べ替えられています
//どの部分が並べ替えられていません
//並べ替える必要がある要素の 1 つを見つけます
//この要素は 2 番目の要素から始まり、並べ替える必要がある最後の要素で終わります
// ループを使用してマークできます
//i ループは毎回挿入する必要がある要素を制御します。挿入する必要がある要素が制御されると、
//間接的に配列が 2 つの部分に分割されます。 、下付き文字は現在より小さいです (左側のもの) はソートされたシーケンスです
for($i=1, $len=count($arr); $私<$ len; $i++) {
// 比較する必要がある現在の要素の値を取得します。
-
$tmp = $arr[ ]; //内部ループ比較と挿入を制御します
-
for
( $j=$i- 1;$j>=0;$ j --) {
//$arr[$i];//挿入される要素; $arr[$j] //比較される要素
- if
( $tmp <$arr[$j]) {
-
- [
]; $arr[$j] = $ tmp;
} else {
//如果碰到不需要移动的元素
//由于是已经排序好是数组,则前面的就不需要再次比较了。
break;
}
}
}
//将这个元素 插入到已经排序好的序列内。
//返回
return $arr;
}
<br/>
ログイン後にコピーログイン後にコピーログイン後にコピー六、希尔排序
介绍:
希尔排序,也称递减增量排序算法,是插入排序的一种高速而稳定的改进版本。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
1、插入排序在对几乎已经排好序的数据操作时, 效率高, 即可以达到线性排序的效率
2、但插入排序一般来说是低效的, 因为插入排序每次只能将数据移动一位>
排序效果:
 <br/>希尔排序其实可以理解是插入排序的一个优化版,它的效率跟增量有关,增量要取多少,根据不同的数组是不同的,所以希尔排序是一个不稳定的排序算法,它的时间复杂度为O(nlogn)到O(n^2)之间,实现代码如下:
<br/>希尔排序其实可以理解是插入排序的一个优化版,它的效率跟增量有关,增量要取多少,根据不同的数组是不同的,所以希尔排序是一个不稳定的排序算法,它的时间复杂度为O(nlogn)到O(n^2)之间,实现代码如下:function shellSort($arr) { $len = count($arr); $stepSize = floor($len / 2); while ($stepSize >= 1) { for ($i = $stepSize; $i < $len; $i++) { if ($arr[$i] < $arr[$i - $stepSize]) { $t = $arr[$i]; $j = $i - $stepSize; while ($j >= 0 && $t < $arr[$j]) { $arr[$j + $stepSize] = $arr[$j]; $j -= $stepSize; } $arr[$j + $stepSize] = $t; } } // 缩小步长,再进行插入排序 $stepSize = floor($stepSize / 2); } return $arr; }$arr = [3,1,13,5,7,11,2,4,14,9,15,6,12,10,8]; print_r(bubbleSort($arr));ログイン後にコピー<br/>
七、归并排序
介绍:
归并排序(Merge sort,台湾译作:合并排序)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(pide and Conquer)的一个非常典型的应用
步骤:
申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
设定两个指针,最初位置分别为两个已经排序序列的起始位置
比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
重复步骤3直到某一指针达到序列尾
将另一序列剩下的所有元素直接复制到合并序列尾
排序效果:
 <br/>归并排序的时间复杂度也是O(nlogn)。原理是:对于两个排序好的数组,分别遍历这两个数组,获取较小的元素插入新的数组中,那么,这么新的数组也会是排序好的。代码如下:
<br/>归并排序的时间复杂度也是O(nlogn)。原理是:对于两个排序好的数组,分别遍历这两个数组,获取较小的元素插入新的数组中,那么,这么新的数组也会是排序好的。代码如下:我们先来看看主函数部分:
//交换函数function swap(array &$arr,$a,$b){ $temp = $arr[$a]; $arr[$a] = $arr[$b]; $arr[$b] = $temp; }//归并算法总函数function MergeSort(array &$arr){ $start = 0; $end = count($arr) - 1; MSort($arr,$start,$end); }ログイン後にコピー在总函数中,我们只调用了一个 MSort() 函数,因为我们要使用递归调用,所以将 MSort() 封装起来。
下面我们来看看 MSort() 函数:
function MSort(array &$arr,$start,$end){ //当子序列长度为1时,$start == $end,不用再分组 if($start < $end){ $mid = floor(($start + $end) / 2); //将 $arr 平分为 $arr[$start - $mid] 和 $arr[$mid+1 - $end] MSort($arr,$start,$mid); //将 $arr[$start - $mid] 归并为有序的$arr[$start - $mid] MSort($arr,$mid + 1,$end); //将 $arr[$mid+1 - $end] 归并为有序的 $arr[$mid+1 - $end] Merge($arr,$start,$mid,$end); //将$arr[$start - $mid]部分和$arr[$mid+1 - $end]部分合并起来成为有序的$arr[$start - $end] } }ログイン後にコピー上面的 MSort() 函数实现将数组分半再分半(直到子序列长度为1),然后将子序列合并起来。
现在是我们的归并操作函数 Merge() :
//归并操作function Merge(array &$arr,$start,$mid,$end){ $i = $start; $j=$mid + 1; $k = $start; $temparr = array(); while($i!=$mid+1 && $j!=$end+1) { if($arr[$i] >= $arr[$j]){ $temparr[$k++] = $arr[$j++]; } else{ $temparr[$k++] = $arr[$i++]; } } //将第一个子序列的剩余部分添加到已经排好序的 $temparr 数组中 while($i != $mid+1){ $temparr[$k++] = $arr[$i++]; } //将第二个子序列的剩余部分添加到已经排好序的 $temparr 数组中 while($j != $end+1){ $temparr[$k++] = $arr[$j++]; } for($i=$start; $i<=$end; $i++){ $arr[$i] = $temparr[$i]; } }ログイン後にコピー到了这里,我们的归并算法就完了。我们调用试试:
$arr = array(9,1,5,8,3,7,4,6,2); MergeSort($arr); var_dump($arr);
ログイン後にコピー相关推荐:
以上がPHP はいくつかの一般的な並べ替えアルゴリズムを実装していますの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7647
7647
 15
15
 1392
1392
 52
52
 91
91
 11
11
 36
36
 110
110
 Ubuntu および Debian 用の PHP 8.4 インストールおよびアップグレード ガイド
Dec 24, 2024 pm 04:42 PM
Ubuntu および Debian 用の PHP 8.4 インストールおよびアップグレード ガイド
Dec 24, 2024 pm 04:42 PM
PHP 8.4 では、いくつかの新機能、セキュリティの改善、パフォーマンスの改善が行われ、かなりの量の機能の非推奨と削除が行われています。 このガイドでは、Ubuntu、Debian、またはその派生版に PHP 8.4 をインストールする方法、または PHP 8.4 にアップグレードする方法について説明します。
 今まで知らなかったことを後悔している 7 つの PHP 関数
Nov 13, 2024 am 09:42 AM
今まで知らなかったことを後悔している 7 つの PHP 関数
Nov 13, 2024 am 09:42 AM
あなたが経験豊富な PHP 開発者であれば、すでにそこにいて、すでにそれを行っていると感じているかもしれません。あなたは、運用を達成するために、かなりの数のアプリケーションを開発し、数百万行のコードをデバッグし、大量のスクリプトを微調整してきました。
 PHP 開発用に Visual Studio Code (VS Code) をセットアップする方法
Dec 20, 2024 am 11:31 AM
PHP 開発用に Visual Studio Code (VS Code) をセットアップする方法
Dec 20, 2024 am 11:31 AM
Visual Studio Code (VS Code とも呼ばれる) は、すべての主要なオペレーティング システムで利用できる無料のソース コード エディター (統合開発環境 (IDE)) です。 多くのプログラミング言語の拡張機能の大規模なコレクションを備えた VS Code は、
 JSON Web Tokens(JWT)とPHP APIでのユースケースを説明してください。
Apr 05, 2025 am 12:04 AM
JSON Web Tokens(JWT)とPHP APIでのユースケースを説明してください。
Apr 05, 2025 am 12:04 AM
JWTは、JSONに基づくオープン標準であり、主にアイデンティティ認証と情報交換のために、当事者間で情報を安全に送信するために使用されます。 1。JWTは、ヘッダー、ペイロード、署名の3つの部分で構成されています。 2。JWTの実用的な原則には、JWTの生成、JWTの検証、ペイロードの解析という3つのステップが含まれます。 3. PHPでの認証にJWTを使用する場合、JWTを生成および検証でき、ユーザーの役割と許可情報を高度な使用に含めることができます。 4.一般的なエラーには、署名検証障害、トークンの有効期限、およびペイロードが大きくなります。デバッグスキルには、デバッグツールの使用とロギングが含まれます。 5.パフォーマンスの最適化とベストプラクティスには、適切な署名アルゴリズムの使用、有効期間を合理的に設定することが含まれます。
 PHPでHTML/XMLを解析および処理するにはどうすればよいですか?
Feb 07, 2025 am 11:57 AM
PHPでHTML/XMLを解析および処理するにはどうすればよいですか?
Feb 07, 2025 am 11:57 AM
このチュートリアルでは、PHPを使用してXMLドキュメントを効率的に処理する方法を示しています。 XML(拡張可能なマークアップ言語)は、人間の読みやすさとマシン解析の両方に合わせて設計された多用途のテキストベースのマークアップ言語です。一般的にデータストレージに使用されます
 母音を文字列にカウントするPHPプログラム
Feb 07, 2025 pm 12:12 PM
母音を文字列にカウントするPHPプログラム
Feb 07, 2025 pm 12:12 PM
文字列は、文字、数字、シンボルを含む一連の文字です。このチュートリアルでは、さまざまな方法を使用してPHPの特定の文字列内の母音の数を計算する方法を学びます。英語の母音は、a、e、i、o、u、そしてそれらは大文字または小文字である可能性があります。 母音とは何ですか? 母音は、特定の発音を表すアルファベットのある文字です。大文字と小文字など、英語には5つの母音があります。 a、e、i、o、u 例1 入力:string = "tutorialspoint" 出力:6 説明する 文字列「TutorialSpoint」の母音は、u、o、i、a、o、iです。合計で6元があります
 PHPでの後期静的結合を説明します(静的::)。
Apr 03, 2025 am 12:04 AM
PHPでの後期静的結合を説明します(静的::)。
Apr 03, 2025 am 12:04 AM
静的結合(静的::) PHPで後期静的結合(LSB)を実装し、クラスを定義するのではなく、静的コンテキストで呼び出しクラスを参照できるようにします。 1)解析プロセスは実行時に実行されます。2)継承関係のコールクラスを検索します。3)パフォーマンスオーバーヘッドをもたらす可能性があります。
 PHPマジックメソッド(__construct、__destruct、__call、__get、__setなど)とは何ですか?
Apr 03, 2025 am 12:03 AM
PHPマジックメソッド(__construct、__destruct、__call、__get、__setなど)とは何ですか?
Apr 03, 2025 am 12:03 AM
PHPの魔法の方法は何ですか? PHPの魔法の方法には次のものが含まれます。1。\ _ \ _コンストラクト、オブジェクトの初期化に使用されます。 2。\ _ \ _リソースのクリーンアップに使用される破壊。 3。\ _ \ _呼び出し、存在しないメソッド呼び出しを処理します。 4。\ _ \ _ get、dynamic属性アクセスを実装します。 5。\ _ \ _セット、動的属性設定を実装します。これらの方法は、特定の状況で自動的に呼び出され、コードの柔軟性と効率を向上させます。




 <br/>
<br/>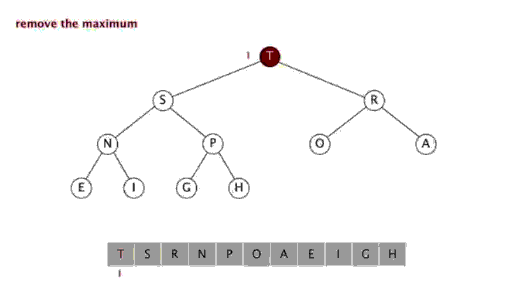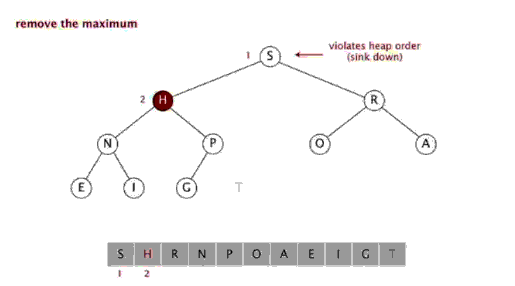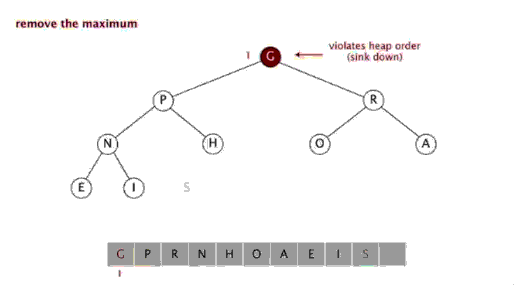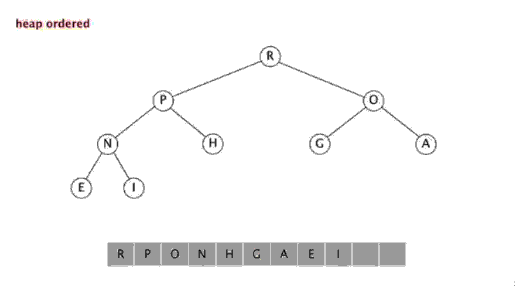
 <br/>
<br/> <br/>感觉插入排序跟冒泡排序有点相似,时间复杂度也是O(n^2),实现代码如下:
<br/>感觉插入排序跟冒泡排序有点相似,时间复杂度也是O(n^2),实现代码如下: <br/>
<br/> <br/>归并排序的时间复杂度也是O(nlogn)。原理是:对于两个排序好的数组,分别遍历这两个数组,获取较小的元素插入新的数组中,那么,这么新的数组也会是排序好的。代码如下:
<br/>归并排序的时间复杂度也是O(nlogn)。原理是:对于两个排序好的数组,分别遍历这两个数组,获取较小的元素插入新的数组中,那么,这么新的数组也会是排序好的。代码如下: