
今回はPythonを使って2次元配列のローカルピーク値を取得する方法を紹介します Pythonを使って2次元配列のローカルピーク値を取得する際の
注意点を紹介します。ケース、見てみましょう。
質問の意味は、大まかに言うと、n*m 個の 2 次元配列内の局所的なピークを見つけることです。ピーク値は、隣接する 4 つの要素よりも大きい必要があります (配列境界の外側は負の無限大とみなされます)。たとえば、最終的にピーク値 A[j][i] が見つかった場合、A[j][i] になります。 ] > A[j+1][i] && A[j][i] > A[j-1][i] > A[j][i+1] && A[j][i] > A[j][i-1]。このピークの座標と値を返します。
もちろん、最も簡単で直接的な方法は、すべての配列要素を走査して、それらがピーク値であるかどうかを判断することです。時間計算量は O(n^2) です 各行の最大値を見つけるためにもう少し最適化します (最大値列のピーク値 (具体的な方法は
1 次元配列ピーク値の検索を参照)、このアルゴリズムの時間計算量は O(logn) です。 ここで説明するのは、複雑度 O(n) のアルゴリズムです。 このアイデアは次のステップに分かれています。
1. 単語「田」を検索します。外側の4つのエッジと中央の縦横2つのエッジ(図の緑色の部分)を含めて、それらの大きさを比較し、最大値の位置を見つけます。
(写真の7)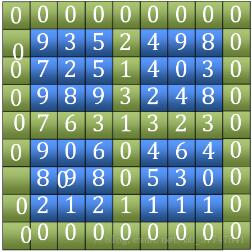
2. 単語Tianの最大値を見つけた後、それがローカルピークであるかどうかを判断し、そうでない場合はその座標を記録します。見つかった 4 つの隣接する点の値の座標のうちの最大値。座標が位置する象限の範囲を縮小し、次のフィールド文字の比較を続けます
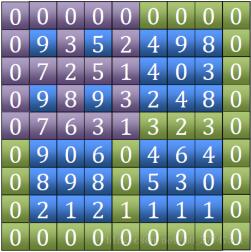
3. 範囲が 3*3 に縮小されると、ローカル ピークが確実に見つかります (または以前に見つかった可能性があります)
なぜ選択した範囲にピークが存在する必要があるかについては、次のように考えることができます。 まず、円が少なくとも 1 つあることがわかっています。円内のすべての要素よりも大きい要素は、この円内に間違いなく 1 つありますか?
少しややこしいかもしれませんが、よく考えれば理解できるはずですし、矛盾による数学的証明を使って証明することもできます。
アルゴリズムを理解したら、次のステップはコードを実装することです。ここで使用する言語は Python です (Python は初めてなので、十分に簡潔でない使用方法があることをご容赦ください)。コード: import numpy as np
def max_sit(*n): #返回最大元素的位置
temp = 0
sit = 0
for i in range(len(n)):
if(n[i]>temp):
temp = n[i]
sit = i
return sit
def dp(s1,s2,e1,e2):
m1 = int((e1-s1)/2)+s1 #row
m2 = int((e2-s1)/2)+s2 #col
nub = e1-s1
temp = 0
sit_row = 0
sit_col = 0
for i in range(nub):
t = max_sit(list[s1][s2+i], #第一排
list[m1][s2+i], #中间排
list[e1][s2+i], #最后排
list[s1+i][s2], #第一列
list[s1+i][m2], #中间列
list[s1+i][e2], #最后列
temp)
if(t==6):
pass
elif(t==0):
temp = list[s1][s2+i]
sit_row = s1
sit_col = s2+i
elif(t==1):
temp = list[m1][s2+i]
sit_row = m1
sit_col = s2+i
elif(t==2):
temp = list[e1][s2+i]
sit_row = e1
sit_col = s2+i
elif(t==3):
temp = list[s1+i][s2]
sit_row = s1+i
sit_row = s2
elif(t==4):
temp = list[s1+i][m2]
sit_row = s1+i
sit_col = m2
elif(t==5):
temp = list[s1+i][e2]
sit_row = s1+i
sit_col = m2
t = max_sit(list[sit_row][sit_col], #中
list[sit_row-1][sit_col], #上
list[sit_row+1][sit_col], #下
list[sit_row][sit_col-1], #左
list[sit_row][sit_col+1]) #右
if(t==0):
return [sit_row-1,sit_col-1]
elif(t==1):
sit_row-=1
elif(t==2):
sit_row+=1
elif(t==3):
sit_col-=1
elif(t==4):
sit_col+=1
if(sit_row<m1):
e1 = m1
else:
s1 = m1
if(sit_col<m2):
e2 = m2
else:
s2 = m2
return dp(s1,s2,e1,e2)
f = open("demo.txt","r")
list = f.read()
list = list.split("\n") #对行进行切片
list = ["0 "*len(list)]+list+["0 "*len(list)] #加上下的围墙
for i in range(len(list)): #对列进行切片
list[i] = list[i].split()
list[i] = ["0"]+list[i]+["0"] #加左右的围墙
list = np.array(list).astype(np.int32)
row_n = len(list)
col_n = len(list[0])
ans_sit = dp(0,0,row_n-1,col_n-1)
print("找到峰值点位于:",ans_sit)
print("该峰值点大小为:",list[ans_sit[0]+1,ans_sit[1]+1])
f.close()
で分割後のリストに空の末尾がない場合は、list.pop()という文を追加する必要はありません。)いくつかの変更は、2 次元配列の周囲に「0」の壁を追加したことです。壁を追加すると、ピーク値を判断するときに境界の問題を考慮する必要がなくなります。
max_sit(*n) 関数は、複数の値の中から最大値の位置を見つけてその位置を返すために使用されます。Python の組み込み max 関数は最大値のみを返すことができるため、やはり自分で記述する必要があります。 *n は不定の長さのパラメーターを表します。これは、この関数を使用して Tian と Ten を比較する必要があるため (ピーク値を決定するため)、dp(s1, s2, e1, e2) 関数の 4 つのパラメーターは startx と見なすことができます。それぞれstarty、endx、endy。つまり、範囲の左上隅と右下隅の座標値を探します。
m1とm2はそれぞれrowとcolの中間値で、単語「tian」の中央です。
def max_sit(*n): #返回最大元素的位置 temp = 0 sit = 0 for i in range(len(n)): if(n[i]>temp): temp = n[i] sit = i return sit
最大値を見つけるために 3 行 3 列の値を比較します。2 次元配列が正方形である必要があることに注意してください。
def dp(s1,s2,e1,e2): m1 = int((e1-s1)/2)+s1 #row m2 = int((e2-s1)/2)+s2 #col
単語Tianの最大値がピーク値かどうかを判断し、隣接する最大値が見つからない
for i in range(nub): t = max_sit(list[s1][s2+i], #第一排 list[m1][s2+i], #中间排 list[e1][s2+i], #最后排 list[s1+i][s2], #第一列 list[s1+i][m2], #中间列 list[s1+i][e2], #最后列 temp) if(t==6): pass elif(t==0): temp = list[s1][s2+i] sit_row = s1 sit_col = s2+i elif(t==1): temp = list[m1][s2+i] sit_row = m1 sit_col = s2+i elif(t==2): temp = list[e1][s2+i] sit_row = e1 sit_col = s2+i elif(t==3): temp = list[s1+i][s2] sit_row = s1+i sit_row = s2 elif(t==4): temp = list[s1+i][m2] sit_row = s1+i sit_row = m2 elif(t==5): temp = list[s1+i][e2] sit_row = s1+i sit_row = m2
範囲を狭めて再帰的に解く
t = max_sit(list[sit_row][sit_col], #中 list[sit_row-1][sit_col], #上 list[sit_row+1][sit_col], #下 list[sit_row][sit_col-1], #左 list[sit_row][sit_col+1]) #右 if(t==0): return [sit_row-1,sit_col-1] elif(t==1): sit_row-=1 elif(t==2): sit_row+=1 elif(t==3): sit_col-=1 elif(t==4): sit_col+=1
さて、ここでコード解析はほぼ完了です。ご不明な点がございましたら、以下にメッセージを残してください。
このアルゴリズムに加えて、この問題を解決するために貪欲なアルゴリズムも作成しました。残念ながら、アルゴリズムの複雑さは最悪の場合でも O(n^2) です (QAQ)。
大体的思路就是从中间位置起找相邻4个点中最大的点,继续把该点来找相邻最大点,最后一定会找到一个峰值点,有兴趣的可以看一下,上代码:
#!/usr/bin/python3
def dp(n):
temp = (str[n],str[n-9],str[n-1],str[n+1],str[n+9]) #中 上 左 右 下
sit = temp.index(max(temp))
if(sit==0):
return str[n]
elif(sit==1):
return dp(n-9)
elif(sit==2):
return dp(n-1)
elif(sit==3):
return dp(n+1)
else:
return dp(n+9)
f = open("/home/nancy/桌面/demo.txt","r")
list = f.read()
list = list.replace(" ","").split() #转换为列表
row = len(list)
col = len(list[0])
str="0"*(col+3)
for x in list: #加围墙 二维变一维
str+=x+"00"
str+="0"*(col+1)
mid = int(len(str)/2)
print(str,mid)
p = dp(mid)
print (p)
f.close()相信看了本文案例你已经掌握了方法,更多精彩请关注php中文网其它相关文章!
推荐阅读:
以上がPythonで2次元配列のローカルピーク値を取得する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。