Python は Jarque-Bera が正規分布に従うかどうかをテストします

この記事の内容は、Jarque-Beraが正規分布に従うかどうかをPythonを使用してテストすることです。必要な友達はそれを参照できます

正規分布は母集団の正規分布です。 . セックステスト。シーケンスが正規分布に従う場合、JB 統計量:

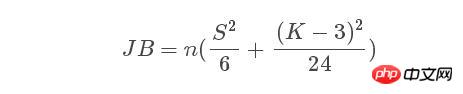
は漸近的に分布に従います。ここで、n はサンプル サイズ、S と K はそれぞれ確率変数の歪度と尖度です。計算式は次のとおりです。

Python の sicipy.stats における歪度と尖度の呼び出しの関数は

で、尖度の式は

Excel では、歪度と尖度の計算式は次のとおりです。

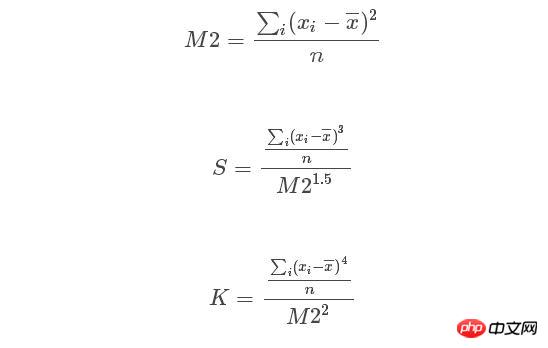
stats.skew(y)、stats.kurtosis(y) Python の scipy ライブラリに歪度と偏りを計算する式を実装し、正規分布テストを確立しましょう。

コード

import numpy as npimport scipy.stats as statsdef self_JBtest(y):
    # 样本规模n
    n = y.size
    y_ = y - y.mean()    """
    M2:二阶中心钜
    skew 偏度 = 三阶中心矩 与 M2^1.5的比
    krut 峰值 = 四阶中心钜 与 M2^2 的比
    """
    M2 = np.mean(y_**2)
    skew =  np.mean(y_**3)/M2**1.5
    krut = np.mean(y_**4)/M2**2

    """
    计算JB统计量，以及建立假设检验
    """
    JB = n*(skew**2/6 + (krut-3 )**2/24)
    pvalue = 1 - stats.chi2.cdf(JB,df=2)
    print("偏度：",stats.skew(y),skew)
    print("峰值：",stats.kurtosis(y)+3,krut)
    print("JB检验：",stats.jarque_bera(y))    return np.array([JB,pvalue])

y1 = stats.norm.rvs(size=10)

y2 = stats.t.rvs(size=1000,df=4)

print(self_JBtest(y1))

print(self_JBtest(y2))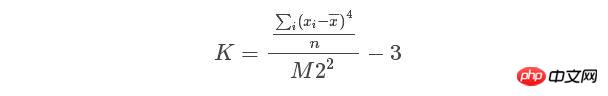

結果

=============== RESTART: C:\Users\tinysoft\Desktop\JB正态性检验.py =============== 

  偏度： 0.5383125387398069 0.53831253874 

  峰值： 2.9948926317585918 2.99489263176 

  JB检验： (0.48297818444514068, 0.78545737133644544) 

  [ 0.48297818  0.78545737] 

  偏度： -1.0488825341925703 -1.04888253419 

  峰值： 13.40804986639119 13.4080498664 

  JB检验： (4697.0050126426095, 0.0) 

  [ 4697.00501264     0.        ]

以上がPython は Jarque-Bera が正規分布に従うかどうかをテストしますの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。