JS二分探索木の使い方を詳しく解説
今回は、JS バイナリ search ツリーの使用方法について詳しく説明します。JS バイナリ サーチ ツリーを使用する際の 注意事項 は何ですか。以下は実際的なケースです。見てみましょう。
二分木とは何ですか
バイナリ ツリーとは、ツリーの各ノードが最大 2 つの子ノードしか持てないことを意味します
二分探索木とは
二分木に基づいて、二分探索木には追加の条件があります。つまり、二分木に値を挿入するとき、挿入された値が現在のノードより小さい場合は左のノードに挿入され、そうでない場合は左のノードに挿入されます。挿入プロセス中に左側のノードが存在する場合は右側のノードに挿入され、右側のノードが既に存在する場合は、新しいノードが見つかるまで上記のルールに従って比較が続けられます。
二分探索木の特徴
その独特なデータ構造により、二分探索木の追加、削除、検索の時間計算量は O(h) です。ここで、h は二分木の高さです。したがって、バイナリ ツリーはできるだけ短くする必要があります。つまり、左右のノードのバランスをできるだけ整える必要があります。
二分探索木の構築
二分探索木を構築するには、まず二分木のノード クラスを構築する必要があります。二分木の特徴から、各ノードクラスには左ノード、右ノード、値そのものがあることがわかり、ノードクラスは次のようになります:
class Node {
constructor(key) {
this.key = key;
this.left = null;
this.right = null;
}
}次に、二分探索木を構築します
class Tree{
constructor(param = null) {
if (param) {
this.root = new Node(param);
} else {
this.root = null;
}
}
}ここで this.root は現在の オブジェクト のツリーです。
二分探索木の新規追加
左側のサブツリーがノードより小さく、右側のサブツリーがノードより大きいという二分探索木の特性に基づいて、二分探索木の新しいアルゴリズムは次のように簡単に記述できます。 上記のコードは、まず、新しく追加されたキーのサイズと現在のノードのキーを決定し、それが現在のノードよりも大きい場合は、null の左の子ノードを見つけるまで再帰的に調べます。同じ原則が当てはまります。上記のコード {1}{2}{3}{4} が this.root の値を変更できる理由は、
JavaScript関数が値によって渡され、パラメーターが非基本型である場合に、ここではオブジェクトとして、そのオブジェクトの値はメモリなので、this.rootの内容は毎回直接変更されます。
二分探索木の走査二分探索ツリーは、preorder、inorder、postorder の 3 つの走査方法に分類されます。
りー上記は順序どおりの走査です。
ここで理解すべきは再帰です。ご存知のとおり、関数の実行はデータ構造、つまりスタックに抽象化できます。関数の実行では、関数の実行を保存するためにスタックが維持されます。関数が再帰するたびに、現在の実行環境がスタックにプッシュされ、実行場所が記録されます。上記のコードを例にすると、次のようなデータがあります
11 から開始し、スタックに対して {1} を実行し、次に 7 に進み、次にスタックに対して {1} を実行します。次に、5 に進み、スタックに対して {1} を実行します。その後、3 に進み、{1 を実行します。このとき、ノード 3 の左側の子ノードが null であることがわかり、ノード 3 の実行環境がポップアップし、{2} を実行します。 {3} を実行すると、3 の右側の子ノードも null であることがわかり、{3} の再帰的実行が完了し、ノード 5 をポップアップして {2}{3} を実行し、次にノード 7 をポップアップして実行します。 {2}{3} をスタックに追加し、{3} を実行すると、ノード 7 に右側のノードがあることが判明したため、{1} の実行を継続し、ノード 8 まで実行します。再度 {1} を実行します。8 には左側の子がありません。ノード、{1} が実行され、{2}{3} が実行されます。
preorder とmidorder の違いは、ノード自体が最初にアクセスされること、つまりコードの実行順序が 2 1 3 であることです。
ポストオーダーも同様で、約定順序は1 3 2です
順序が前、中、後であっても、左のノードが常に最初に再帰され、左のノードが走査されると、スタックがポップされ、すべてのノードが走査されることを見つけるのは難しくありません。それらの唯一の違いは、ノード自体にアクセスするタイミングです。
二分探索木探索
探索は非常に簡単で、左の子ノードがそのノードより小さく、右の子ノードがそのノードより大きいという原則に基づいてループ判定するだけです。
りー二分探索木の
削除削除はより複雑であり、さまざまな状況に応じて判断する必要があります
まず、ノードに左側のサブツリーがあるかどうかを確認します。左側のサブツリーがない場合は、削除されたノードを右側のサブツリーのルート ノードに直接置き換えます。 存在する場合は、削除されたノードを右のサブツリーの最小のノードに置き換えます
;remove(key) {
this._removeNode(this.root, key);
}
_removeNode(node, value) {
if (!node) {
return null;
}
if (value > node.key) {
node.right = this._removeNode(node.right, value);
} else if (value < node.key) {
node.left = this._removeNode(node.left, value);
} else {
// 如果没有左子树,那么将右子树根节点作为替换节点
if (!node.left) {
return node.right;
// 如果存在左子树,那么取右子树最小节点作为替换节点
} else if (node.left) {
return this._minNode(node.right);
}
}
}总结
总的来说,通过这次简单的二叉搜索树的学习,让我重新认识了递归,以前对于递归的理解只是一些简单的理论概念,这次深入实践让我对递归的理解又加深了许多。
这让我想到了数学的学习,数学的理论公式是很容易记住掌握的,如果说对一个知识点的掌握满分是十分,那么直到真正去实践它之前,只看公式的掌握只能是2分,因为公式很简单,就几句话几个原则,但是遇到的问题是千变万化的,只有真正将理论付诸实践,经过各种实践的打磨蹂躏,才能真正理解它其中的奥秘。
相信看了本文案例你已经掌握了方法,更多精彩请关注php中文网其它相关文章!
推荐阅读:
以上がJS二分探索木の使い方を詳しく解説の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7615
7615
 15
15
 1387
1387
 52
52
 88
88
 11
11
 29
29
 136
136
 CrystalDiskmarkとはどのようなソフトウェアですか? -crystaldiskmarkの使い方は?
Mar 18, 2024 pm 02:58 PM
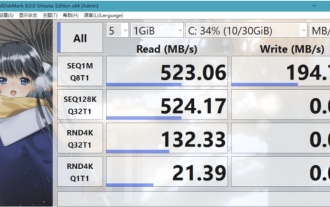
CrystalDiskmarkとはどのようなソフトウェアですか? -crystaldiskmarkの使い方は?
Mar 18, 2024 pm 02:58 PM
CrystalDiskMark は、シーケンシャルおよびランダムの読み取り/書き込み速度を迅速に測定する、ハード ドライブ用の小型 HDD ベンチマーク ツールです。次に、編集者が CrystalDiskMark と Crystaldiskmark の使用方法を紹介します。 1. CrystalDiskMark の概要 CrystalDiskMark は、機械式ハード ドライブとソリッド ステート ドライブ (SSD) の読み取りおよび書き込み速度とパフォーマンスを評価するために広く使用されているディスク パフォーマンス テスト ツールです。 ). ランダム I/O パフォーマンス。これは無料の Windows アプリケーションで、使いやすいインターフェイスとハード ドライブのパフォーマンスのさまざまな側面を評価するためのさまざまなテスト モードを提供し、ハードウェアのレビューで広く使用されています。
 foobar2000のダウンロード方法は? -foobar2000の使い方
Mar 18, 2024 am 10:58 AM
foobar2000のダウンロード方法は? -foobar2000の使い方
Mar 18, 2024 am 10:58 AM
foobar2000 は、音楽リソースをいつでも聴くことができるソフトウェアです。あらゆる種類の音楽をロスレス音質で提供します。音楽プレーヤーの強化版により、より包括的で快適な音楽体験を得ることができます。その設計コンセプトは、高度なオーディオをコンピュータ上で再生可能 デバイスを携帯電話に移植し、より便利で効率的な音楽再生体験を提供 シンプルでわかりやすく、使いやすいインターフェースデザイン 過度な装飾や煩雑な操作を排除したミニマルなデザインスタイルを採用また、さまざまなスキンとテーマをサポートし、自分の好みに合わせて設定をカスタマイズし、複数のオーディオ形式の再生をサポートする専用の音楽プレーヤーを作成します。過度の音量による聴覚障害を避けるために、自分の聴覚の状態に合わせて調整してください。次は私がお手伝いさせてください
 NetEase メールボックス マスターの使用方法
Mar 27, 2024 pm 05:32 PM
NetEase メールボックス マスターの使用方法
Mar 27, 2024 pm 05:32 PM
NetEase Mailbox は、中国のネットユーザーに広く使用されている電子メール アドレスとして、その安定した効率的なサービスで常にユーザーの信頼を獲得してきました。 NetEase Mailbox Master は、携帯電話ユーザー向けに特別に作成された電子メール ソフトウェアで、電子メールの送受信プロセスが大幅に簡素化され、電子メールの処理がより便利になります。 NetEase Mailbox Master の使い方と具体的な機能について、以下ではこのサイトの編集者が詳しく紹介しますので、お役に立てれば幸いです。まず、モバイル アプリ ストアで NetEase Mailbox Master アプリを検索してダウンロードします。 App Store または Baidu Mobile Assistant で「NetEase Mailbox Master」を検索し、画面の指示に従ってインストールします。ダウンロードとインストールが完了したら、NetEase の電子メール アカウントを開いてログインします。ログイン インターフェイスは次のとおりです。
 Baidu Netdisk アプリの使用方法
Mar 27, 2024 pm 06:46 PM
Baidu Netdisk アプリの使用方法
Mar 27, 2024 pm 06:46 PM
クラウド ストレージは今日、私たちの日常生活や仕事に欠かせない部分になっています。中国有数のクラウド ストレージ サービスの 1 つである Baidu Netdisk は、強力なストレージ機能、効率的な伝送速度、便利な操作体験により多くのユーザーの支持を得ています。また、重要なファイルのバックアップ、情報の共有、オンラインでのビデオの視聴、または音楽の聴きたい場合でも、Baidu Cloud Disk はニーズを満たすことができます。しかし、Baidu Netdisk アプリの具体的な使用方法を理解していないユーザーも多いため、このチュートリアルでは Baidu Netdisk アプリの使用方法を詳しく紹介します。まだ混乱しているユーザーは、この記事に従って詳細を学ぶことができます。 Baidu Cloud Network Disk の使用方法: 1. インストール まず、Baidu Cloud ソフトウェアをダウンロードしてインストールするときに、カスタム インストール オプションを選択してください。
 Win11での管理者権限の取得について詳しく解説
Mar 08, 2024 pm 03:06 PM
Win11での管理者権限の取得について詳しく解説
Mar 08, 2024 pm 03:06 PM
Windows オペレーティング システムは世界で最も人気のあるオペレーティング システムの 1 つであり、その新バージョン Win11 が大きな注目を集めています。 Win11 システムでは、管理者権限の取得は重要な操作であり、管理者権限を取得すると、ユーザーはシステム上でより多くの操作や設定を実行できるようになります。この記事では、Win11システムで管理者権限を取得する方法と、権限を効果的に管理する方法を詳しく紹介します。 Win11 システムでは、管理者権限はローカル管理者とドメイン管理者の 2 種類に分かれています。ローカル管理者はローカル コンピュータに対する完全な管理権限を持っています
 BTCC チュートリアル: BTCC 取引所で MetaMask ウォレットをバインドして使用する方法は?
Apr 26, 2024 am 09:40 AM
BTCC チュートリアル: BTCC 取引所で MetaMask ウォレットをバインドして使用する方法は?
Apr 26, 2024 am 09:40 AM
MetaMask (中国語ではリトル フォックス ウォレットとも呼ばれます) は、無料で評判の高い暗号化ウォレット ソフトウェアです。現在、BTCC は MetaMask ウォレットへのバインドをサポートしており、バインド後は MetaMask ウォレットを使用してすぐにログイン、値の保存、コインの購入などが可能になり、初回バインドで 20 USDT のトライアル ボーナスも獲得できます。 BTCCMetaMask ウォレットのチュートリアルでは、MetaMask の登録方法と使用方法、および BTCC で Little Fox ウォレットをバインドして使用する方法を詳しく紹介します。メタマスクウォレットとは何ですか? 3,000 万人を超えるユーザーを抱える MetaMask Little Fox ウォレットは、現在最も人気のある暗号通貨ウォレットの 1 つです。無料で使用でき、拡張機能としてネットワーク上にインストールできます。
 Oracle SQLの除算演算の詳細説明
Mar 10, 2024 am 09:51 AM
Oracle SQLの除算演算の詳細説明
Mar 10, 2024 am 09:51 AM
OracleSQL の除算演算の詳細な説明 OracleSQL では、除算演算は一般的かつ重要な数学演算であり、2 つの数値を除算した結果を計算するために使用されます。除算はデータベース問合せでよく使用されるため、OracleSQL での除算演算とその使用法を理解することは、データベース開発者にとって重要なスキルの 1 つです。この記事では、OracleSQL の除算演算に関する関連知識を詳細に説明し、読者の参考となる具体的なコード例を示します。 1. OracleSQL での除算演算
 iOS 17.4の新しい高度な機能「盗難デバイス保護」の使い方を教えます
Mar 10, 2024 pm 04:34 PM
iOS 17.4の新しい高度な機能「盗難デバイス保護」の使い方を教えます
Mar 10, 2024 pm 04:34 PM
Appleは火曜日にiOS 17.4アップデートを公開し、iPhoneに多数の新機能と修正をもたらした。このアップデートには新しい絵文字が含まれており、EU ユーザーは他のアプリ ストアから絵文字をダウンロードすることもできます。さらに、このアップデートでは iPhone のセキュリティ制御も強化され、より多くの「盗難デバイス保護」設定オプションが導入され、ユーザーにより多くの選択肢と保護が提供されます。 「iOS17.3では、「盗難デバイス保護」機能が初めて導入され、ユーザーの機密情報のセキュリティが強化されています。ユーザーが自宅やその他の身近な場所から離れている場合、この機能ではユーザーは最初に生体認証情報を入力する必要がありますApple ID パスワードの変更や盗難デバイス保護の無効化など、特定のデータにアクセスして変更するには、情報を再度入力する必要があります。




