再帰アルゴリズムに基づいて Python で実装されたハノイの塔とフィボナッチ数列
この記事では、主に再帰アルゴリズムに基づいて Python で実装されたハノイの塔とフィボナッチ数列を紹介します。ハノイの塔とフィボナッチ数列の再帰実装テクニックをサンプルの形式で分析します。
この記事では、ハノイの塔と再帰アルゴリズムによって実装されたフィボナッチ数列に基づく Python の例について説明します。参考のために皆さんと共有してください。詳細は次のとおりです:
ここでは 2 つの例を使用して、Python での再帰の使用法を学びます。
1. フィボナッチ数列で添え字 n を持つ数値を見つけます (添え字は 0 から数えます)
フィボナッチ数列の形式は次のとおりです: 0,1,1,2,3,5,8 ,13...
① while ループを使用すると、Python2 コードは次のようになります。
def fib(n):
a,b=0,1
count=0
while count<n:
a,b=b,a+b
count=count+1
print a実行結果は次のようになります。
② 再帰を使用する (再帰には境界条件が必要です)>>>
0
>> fib(1)
1
>>> fib(3)
2
> 4)
3
> >> fib(5)
5
の Python2 コードは次のとおりです。実行結果は次のとおりです:
>> ;> fib(0)0
>>> fib(2)
> >> fib(3)
2
3
>>> fib(5)下の写真は、プレートが4枚だけのハノイの塔ゲームの簡易版です:
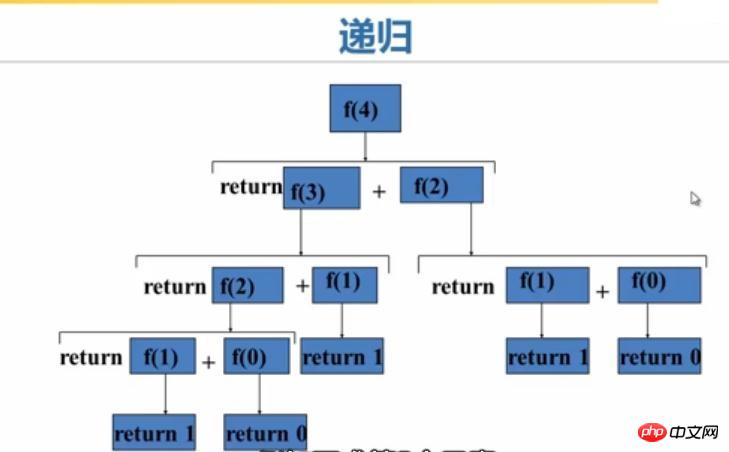
再帰は計算的思考を最もよく表現するアルゴリズムの 1 つです例として f(4) を見てみましょう:
同じプログラムは再帰を使用しますが、プログラムは単純ですが、再帰の実行効率はループよりも低くなります。システムリソースの消費量はループよりも大きくなります。再帰は階層ごとに呼び出され、完了後に階層ごとに返されるため、再帰の実行効率は高くありません。では、なぜ再帰を使用するのでしょうか?いくつかの問題があるため、明確なループ解決策を見つけることはできませんが、明確な再帰的解決策を見つけるのは簡単です。有名なハノイ塔問題を例に考えてみましょう。
2. ハノイの塔
Python2のコードは次のとおりです:
def fib(n):
if n==0 or n==1:#递归的边界条件
return n
else:
return fib(n-1)+fib(n-2)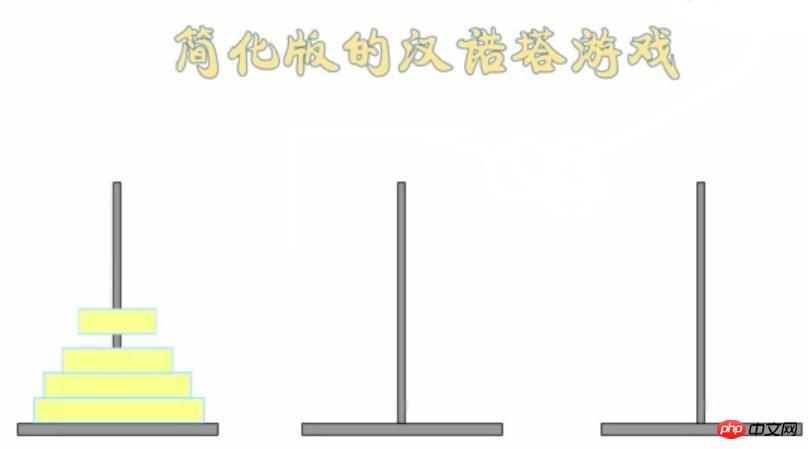
>>> hanoi('A','B','C',1) A ->C
A ->C
A->C
>> > ハノイ('A','B','C',3)A -> C
B ->C
関連する推奨事項:
ニューラルネットワーク (BP) アルゴリズムの Python 実装とアプリケーション
以上が再帰アルゴリズムに基づいて Python で実装されたハノイの塔とフィボナッチ数列の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7569
7569
 15
15
 1386
1386
 52
52
 87
87
 11
11
 28
28
 107
107
 PHPおよびPython:コードの例と比較
Apr 15, 2025 am 12:07 AM
PHPおよびPython:コードの例と比較
Apr 15, 2025 am 12:07 AM
PHPとPythonには独自の利点と短所があり、選択はプロジェクトのニーズと個人的な好みに依存します。 1.PHPは、大規模なWebアプリケーションの迅速な開発とメンテナンスに適しています。 2。Pythonは、データサイエンスと機械学習の分野を支配しています。
 Python vs. JavaScript:コミュニティ、ライブラリ、リソース
Apr 15, 2025 am 12:16 AM
Python vs. JavaScript:コミュニティ、ライブラリ、リソース
Apr 15, 2025 am 12:16 AM
PythonとJavaScriptには、コミュニティ、ライブラリ、リソースの観点から、独自の利点と短所があります。 1)Pythonコミュニティはフレンドリーで初心者に適していますが、フロントエンドの開発リソースはJavaScriptほど豊富ではありません。 2)Pythonはデータサイエンスおよび機械学習ライブラリで強力ですが、JavaScriptはフロントエンド開発ライブラリとフレームワークで優れています。 3)どちらも豊富な学習リソースを持っていますが、Pythonは公式文書から始めるのに適していますが、JavaScriptはMDNWebDocsにより優れています。選択は、プロジェクトのニーズと個人的な関心に基づいている必要があります。
 ターミナルVSCODEでプログラムを実行する方法
Apr 15, 2025 pm 06:42 PM
ターミナルVSCODEでプログラムを実行する方法
Apr 15, 2025 pm 06:42 PM
VSコードでは、次の手順を通じて端末でプログラムを実行できます。コードを準備し、統合端子を開き、コードディレクトリが端末作業ディレクトリと一致していることを確認します。プログラミング言語(pythonのpython your_file_name.pyなど)に従って実行コマンドを選択して、それが正常に実行されるかどうかを確認し、エラーを解決します。デバッガーを使用して、デバッグ効率を向上させます。
 Visual StudioコードはPythonで使用できますか
Apr 15, 2025 pm 08:18 PM
Visual StudioコードはPythonで使用できますか
Apr 15, 2025 pm 08:18 PM
VSコードはPythonの書き込みに使用でき、Pythonアプリケーションを開発するための理想的なツールになる多くの機能を提供できます。ユーザーは以下を可能にします。Python拡張機能をインストールして、コードの完了、構文の強調表示、デバッグなどの関数を取得できます。デバッガーを使用して、コードを段階的に追跡し、エラーを見つけて修正します。バージョンコントロールのためにGitを統合します。コードフォーマットツールを使用して、コードの一貫性を維持します。糸くずツールを使用して、事前に潜在的な問題を発見します。
 Dockerの原則の詳細な説明
Apr 14, 2025 pm 11:57 PM
Dockerの原則の詳細な説明
Apr 14, 2025 pm 11:57 PM
DockerはLinuxカーネル機能を使用して、効率的で孤立したアプリケーションランニング環境を提供します。その作業原則は次のとおりです。1。ミラーは、アプリケーションを実行するために必要なすべてを含む読み取り専用テンプレートとして使用されます。 2。ユニオンファイルシステム(UnionFS)は、違いを保存するだけで、スペースを節約し、高速化する複数のファイルシステムをスタックします。 3.デーモンはミラーとコンテナを管理し、クライアントはそれらをインタラクションに使用します。 4。名前空間とcgroupsは、コンテナの分離とリソースの制限を実装します。 5.複数のネットワークモードは、コンテナの相互接続をサポートします。これらのコア概念を理解することによってのみ、Dockerをよりよく利用できます。
 VSCODE拡張機能は悪意がありますか?
Apr 15, 2025 pm 07:57 PM
VSCODE拡張機能は悪意がありますか?
Apr 15, 2025 pm 07:57 PM
VSコード拡張機能は、悪意のあるコードの隠れ、脆弱性の活用、合法的な拡張機能としての自慰行為など、悪意のあるリスクを引き起こします。悪意のある拡張機能を識別する方法には、パブリッシャーのチェック、コメントの読み取り、コードのチェック、およびインストールに注意してください。セキュリティ対策には、セキュリティ認識、良好な習慣、定期的な更新、ウイルス対策ソフトウェアも含まれます。
 Windows 8でコードを実行できます
Apr 15, 2025 pm 07:24 PM
Windows 8でコードを実行できます
Apr 15, 2025 pm 07:24 PM
VSコードはWindows 8で実行できますが、エクスペリエンスは大きくない場合があります。まず、システムが最新のパッチに更新されていることを確認してから、システムアーキテクチャに一致するVSコードインストールパッケージをダウンロードして、プロンプトとしてインストールします。インストール後、一部の拡張機能はWindows 8と互換性があり、代替拡張機能を探すか、仮想マシンで新しいWindowsシステムを使用する必要があることに注意してください。必要な拡張機能をインストールして、適切に動作するかどうかを確認します。 Windows 8ではVSコードは実行可能ですが、開発エクスペリエンスとセキュリティを向上させるために、新しいWindowsシステムにアップグレードすることをお勧めします。
 Python:自動化、スクリプト、およびタスク管理
Apr 16, 2025 am 12:14 AM
Python:自動化、スクリプト、およびタスク管理
Apr 16, 2025 am 12:14 AM
Pythonは、自動化、スクリプト、およびタスク管理に優れています。 1)自動化:OSやShutilなどの標準ライブラリを介してファイルバックアップが実現されます。 2)スクリプトの書き込み:Psutilライブラリを使用してシステムリソースを監視します。 3)タスク管理:スケジュールライブラリを使用してタスクをスケジュールします。 Pythonの使いやすさと豊富なライブラリサポートにより、これらの分野で優先ツールになります。




