Python は LR クラシック アルゴリズムを実装します
この記事の例では、Python での LR クラシック アルゴリズムの実装について説明します。皆さんにも共有して参考にしてください。詳細は以下のとおりです。
(1) ロジスティック回帰 (LR) 分類器を理解する
まず、ロジスティック回帰は名前に「回帰」が付いていますが、 、実際には分類方法であり、主に 2 分類問題に使用され、ロジスティック関数 (またはシグモイド関数) を使用します。独立変数の値の範囲は (-INF, INF)、独立変数の値の範囲は ( 0,1)、関数形式は次のとおりです:

シグモイド関数の定義域は (-INF, +INF) であるため、値の範囲は (0, 1) です。 )。したがって、最も基本的な LR 分類器は、2 つのカテゴリ (クラス 0、クラス 1) のターゲットを分類するのに適しています。シグモイド関数は、以下の図に示すように、非常に美しい「S」字型です。

LR 分類器 (ロジスティック回帰分類器) の目的は、0/1 分類を学習することです。トレーニング データの特徴からのモデル -- このモデルは、サンプル特徴  の線形結合を独立変数として使用し、ロジスティック関数を使用して独立変数を (0,1) にマッピングします。したがって、LR 分類器の解決策は、一連の重み
の線形結合を独立変数として使用し、ロジスティック関数を使用して独立変数を (0,1) にマッピングします。したがって、LR 分類器の解決策は、一連の重み  を解くことです (
を解くことです ( は名目上の変数、つまり定数です。実際のエンジニアリングでは、x0=1.0 がよく使用されます。定数項が意味があるかどうかは関係ありません)またはそうでない場合は、保持するのが最善です) をロジスティック関数に代入します。 予測関数を構築します:
は名目上の変数、つまり定数です。実際のエンジニアリングでは、x0=1.0 がよく使用されます。定数項が意味があるかどうかは関係ありません)またはそうでない場合は、保持するのが最善です) をロジスティック関数に代入します。 予測関数を構築します: 
関数の値は、結果が 1 になる確率を表します。特徴は y=1 に属します。したがって、入力に対して Z 値を検索します:
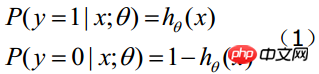 (x1,x2,...,xn は特定のサンプル データの特徴であり、次元は n)
(x1,x2,...,xn は特定のサンプル データの特徴であり、次元は n)
その後、
ロジスティック回帰も多クラス分類に使用できますが、二値分類の方が一般的に使用され、説明が簡単です。したがって、実際に最も一般的に使用されるのは 2 項ロジスティック回帰です。 LR 分類子は、数値データと公称データのデータ タイプに適しています。その利点は、計算コストが高くなく、理解および実装が簡単であることですが、欠点は、アンダーフィットしやすく、分類精度が高くない可能性があることです。 まず、次の数学的導出プロセスを理解するには、より多くの導関数の解公式が必要です。 「基本的な初等関数でよく使われる微分公式と積分公式」を参照できます。 n 個の観測サンプルがあり、観測値が を取得するための包括的な式 (1) です。各観測値は独立しているため、それらの同時分布は次のように表すことができます。分布: 的 (テーブル統計サンプルの数) 上の式は N 観測尤度関数と呼ばれます。私たちの目標は、この尤度関数の値を最大化するパラメータ推定値を見つけられるようにすることです。したがって、最尤推定の鍵は、上式が最大値になるようにパラメータ を見つけることです。 上記の関数の対数を求めます。 最尤推定は、上記の方程式が最大値をとるときの θ を見つけることです。 ここでは、勾配上昇法を使用できます。それを解くために必要な最適パラメータは θ です。 Andrew Ng のコースでは、J(θ) は次の式として扱われます。つまり、J(θ)=-(1/m)l(θ) であり、J(θ) が最小になるときの θ が必要な最適値となります。パラメータ。勾配降下法により最小値を求めます。 θ の初期値はすべて 1.0 であり、更新プロセスは次のとおりです: (j はサンプルの j 番目の属性、合計 n を表します。a はステップ サイズ、つまり各動きのサイズを表します)自由に指定可能) したがって、θの更新処理(初期値はすべて1.0に設定できます)は次のように記述できます。 この式は、収束に達するまで繰り返し実行されます ( ベクトル化では、for ループの代わりに行列計算を使用して、計算プロセスを簡素化し、効率を向上させます。上の式に示されているように、Σ(...) は合計処理であり、明らかに for ステートメントを m 回ループする必要があるため、ベクトル化は完全に実装されていません。ベクトル化のプロセスを以下に紹介します。 トレーニング データの行列形式は次のとおりであることが合意されています。 g(A) のパラメーター A は列ベクトルなので、g 関数を実装するとき。の場合、列ベクトルをパラメーターとしてサポートし、列ベクトルを返す必要があります。上式から、g(A)-y から hθ(x)-y を 1 ステップで計算できることがわかります。
まとめると、ベクトル化後の θ 更新の手順は次のとおりです。
3、ステップ
a の選択も、勾配降下法を確実に収束させるための重要なポイントです。値が小さすぎると収束が遅くなり、値が大きすぎると反復プロセスの収束 (最小値を通過する) が保証されなくなります。勾配降下法アルゴリズムが正しく動作することを保証するには、反復ごとに J(θ) が確実に減少するようにする必要があります。ステップ サイズ a の値が正しければ、J(θ) はどんどん小さくなるはずです。したがって、a の値を判断する基準は、J(θ) が小さくなればその値は正しいことを示し、そうでなければ a の値を小さくすることになります。 ステップ サイズ a を選択する経験は次のとおりです。反復が正常に続行できない場合 (J が増加すると、ステップ サイズが大きすぎ、ボウルの底を超えてしまいます)、毎回、前の数値の約 3 倍の値を選択します。 )、収束が遅い場合は、より小さいステップ サイズの使用を検討してください。値の例は、 …、0.001、0.003、0.01、0.03、0.1、0.3、1…です。 ロジスティック回帰は、勾配法を使用して多次元特徴トレーニングデータを回帰する場合、その固有値をスケーリングして、その値の範囲を確保する必要があります。計算プロセスは同じスケール内でのみ収束します (特徴値の値の範囲は大きく異なる場合があるため、たとえば、特徴 1 の値は (1000-2000)、特徴 2 の値は (1000-2000) です。 (0.1-0.2))。特徴スケーリングの方法はカスタマイズできます: 1) 平均正規化 (または標準化) (X - means(X))/std(X)、std(X) は、サンプルの標準 差 2) リスケーリング (X - min) / (max - min) 勾配上昇 (下降) ) それぞれのアルゴリズム 回帰係数を更新するたびに、データ セット全体を走査する必要があります。この方法は、約 100 のデータ セットを処理する場合には許容できますが、数十億のサンプルと数万の特徴がある場合、この方法の計算は複雑すぎます。高い。 。改良された方法は、一度に 1 つのサンプル ポイントのみを使用して回帰係数を更新することであり、これは確率的勾配アルゴリズムと呼ばれます。新しいサンプルが到着すると分類器は段階的に更新できるため、バッチ処理のためにデータ セット全体を再度読み取る必要がなく、新しいデータが到着するとパラメーターの更新を完了できます。したがって、確率的勾配アルゴリズムはオンライン学習アルゴリズムです。 (「オンライン学習」に相当し、全てのデータを一度に処理することを「バッチ処理」といいます。)確率的勾配アルゴリズムは勾配アルゴリズムと同等ですが、計算効率がより優れています。 前のセクションでは、Andrew Ng のアルゴリズムを通じて J(θ)=-(1/m)l(θ) を解く勾配降下法を使用したロジスティック回帰について説明しました。もちろん、このセクションの Python の解法プロセスでは、J(θ) を解くために勾配上昇法または確率的勾配上昇法を直接使用します。LRTrain オブジェクトも問題を解決するために勾配上昇法または確率的勾配上昇法を実装します。 LR 分類器学習パッケージには、lr.py/object_json.py/test.py の 3 つのモジュールが含まれています。 lr モジュールは、オブジェクト logisticRegres を通じて LR 分類器を実装し、gradAscent('Grad') と randomGradAscent('randomGrad') という 2 つのソリューション メソッドをサポートします (2 つのうちの 1 つを選択します。classifierArray は 1 つの分類ソリューション結果のみを保存します。もちろん、保存することもできます) 2 つの classifierArray を定義すると、両方の解決方法がサポートされます)。 このテスト モジュールは、LR 分類器を使用してヘルニアの症状に基づいて病気の馬の死亡率を予測するアプリケーションです。このデータには問題があります。このデータには 30% の損失率があり、0 は LR 分類器の重み更新に影響を与えないため、特別な値 0 に置き換えられます。 トレーニングデータ内のサンプル特徴値の部分的な欠落は非常に厄介な問題であり、データを直接捨てるのは残念であり、コストもかかるため、多くの文献がこの問題の解決に注力しています。それを再取得します。欠損データを処理するためのオプションの方法には次のものがあります。 □ 欠損値を埋めるために利用可能な特徴の平均を使用します。 □ 欠損値を修正するには、 □ 欠損値のあるサンプルを無視します。 □ 類似したサンプルの平均を使用して欠損値を埋めます。 □ 別の機械学習アルゴリズムを使用して欠損値を予測します。 LR分類器アルゴリズム学習パッケージのダウンロードアドレスは: ロジスティック回帰の主な用途: 探しています危険因子の場合: 特定の病気などの危険因子を探します。 予測: モデルに従って、さまざまな独立変数の下で特定の病気または状況の確率を予測します。 識別: 上記。これは、ある人が特定の病気または特定の状態に属する確率を決定する、つまり、その人が特定の病気に属する可能性を確認するためのモデルにもある程度似ています。 ロジスティック回帰は主に疫学で使用され、特定の病気の危険因子を調査したり、危険因子に基づいて特定の病気の確率を予測したりする場合に使用されます。たとえば、胃がんの危険因子を調査したい場合は、2 つのグループの人々を選択できます。1 つは胃がんグループ、もう 1 つは非胃がんグループです。この 2 つのグループの人々は、異なる身体的特性を持っている必要があります。サインとライフスタイル。ここでの従属変数は、胃がんであるかどうか、つまり「はい」か「いいえ」です。独立変数には、年齢、性別、食習慣、ヘリコバクター・ピロリ感染など、多くの変数が含まれます。独立変数は連続変数またはカテゴリ変数のいずれかになります。
(2) ロジスティック回帰の数学的導出
1. ロジスティック回帰を解くための勾配降下法
 であるとします。
であるとします。  を与えられた条件下で yi=1 になる確率とします。同じ条件下で yi=0 になる条件付き確率は
を与えられた条件下で yi=1 になる確率とします。同じ条件下で yi=0 になる条件付き確率は  です。したがって、観測値を取得する確率は
です。したがって、観測値を取得する確率は 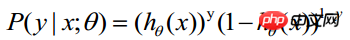 -----この式は実際には
-----この式は実際には 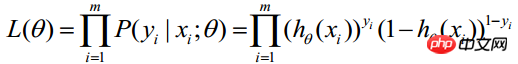

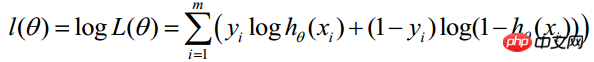
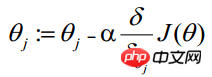

 (i は i 番目の統計サンプルを表し、j はサンプルの j 番目の属性を表します。a はステップ サイズを表します)
(i は i 番目の統計サンプルを表し、j はサンプルの j 番目の属性を表します。a はステップ サイズを表します)


 ) 各ステップでの反復中に減少します。あるステップの減少値が非常に小さい値
) 各ステップでの反復中に減少します。あるステップの減少値が非常に小さい値  より小さい場合 (0.001 未満)、収束していると判断されます)、または特定の停止条件 (たとえば、反復回数が特定の指定値に達するか、アルゴリズムが特定の許容誤差範囲に達します)。
より小さい場合 (0.001 未満)、収束していると判断されます)、または特定の停止条件 (たとえば、反復回数が特定の指定値に達するか、アルゴリズムが特定の許容誤差範囲に達します)。 2、ベクトル化ソリューション
 θ 更新プロセスは次のように変更できます:
θ 更新プロセスは次のように変更できます: 
(1)探すA=X *θ(ここでは行列の乗算、 ) E=g(A)-y を求めます (E、y は (m,1) 次元の列ベクトルです)
(3) 
4、固有値の正規化
5、アルゴリズムの最適化 - 確率的勾配法
(3) Python でのロジスティック回帰アルゴリズムの実装
機械学習 ロジスティック回帰
(4) ロジスティック回帰アプリケーション
関連する推奨事項:
以上がPython は LR クラシック アルゴリズムを実装しますの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7488
7488
 15
15
 1377
1377
 52
52
 77
77
 11
11
 19
19
 40
40
 mysqlは支払う必要がありますか
Apr 08, 2025 pm 05:36 PM
mysqlは支払う必要がありますか
Apr 08, 2025 pm 05:36 PM
MySQLには、無料のコミュニティバージョンと有料エンタープライズバージョンがあります。コミュニティバージョンは無料で使用および変更できますが、サポートは制限されており、安定性要件が低く、技術的な能力が強いアプリケーションに適しています。 Enterprise Editionは、安定した信頼性の高い高性能データベースを必要とするアプリケーションに対する包括的な商業サポートを提供し、サポートの支払いを喜んでいます。バージョンを選択する際に考慮される要因には、アプリケーションの重要性、予算編成、技術スキルが含まれます。完璧なオプションはなく、最も適切なオプションのみであり、特定の状況に応じて慎重に選択する必要があります。
 インストール後にMySQLの使用方法
Apr 08, 2025 am 11:48 AM
インストール後にMySQLの使用方法
Apr 08, 2025 am 11:48 AM
この記事では、MySQLデータベースの操作を紹介します。まず、MySQLWorkBenchやコマンドラインクライアントなど、MySQLクライアントをインストールする必要があります。 1. mysql-uroot-pコマンドを使用してサーバーに接続し、ルートアカウントパスワードでログインします。 2。CreatedAtaBaseを使用してデータベースを作成し、データベースを選択します。 3. createTableを使用してテーブルを作成し、フィールドとデータ型を定義します。 4. INSERTINTOを使用してデータを挿入し、データをクエリし、更新することでデータを更新し、削除してデータを削除します。これらの手順を習得することによってのみ、一般的な問題に対処することを学び、データベースのパフォーマンスを最適化することでMySQLを効率的に使用できます。
 MongoDBデータベースパスワードを表示するNAVICATの方法
Apr 08, 2025 pm 09:39 PM
MongoDBデータベースパスワードを表示するNAVICATの方法
Apr 08, 2025 pm 09:39 PM
Hash値として保存されているため、Navicatを介してMongoDBパスワードを直接表示することは不可能です。紛失したパスワードを取得する方法:1。パスワードのリセット。 2。構成ファイルを確認します(ハッシュ値が含まれる場合があります)。 3.コードを確認します(パスワードをハードコードできます)。
 mysqlはインターネットが必要ですか?
Apr 08, 2025 pm 02:18 PM
mysqlはインターネットが必要ですか?
Apr 08, 2025 pm 02:18 PM
MySQLは、基本的なデータストレージと管理のためにネットワーク接続なしで実行できます。ただし、他のシステムとのやり取り、リモートアクセス、または複製やクラスタリングなどの高度な機能を使用するには、ネットワーク接続が必要です。さらに、セキュリティ対策(ファイアウォールなど)、パフォーマンスの最適化(適切なネットワーク接続を選択)、およびデータバックアップは、インターネットに接続するために重要です。
 高負荷アプリケーションのMySQLパフォーマンスを最適化する方法は?
Apr 08, 2025 pm 06:03 PM
高負荷アプリケーションのMySQLパフォーマンスを最適化する方法は?
Apr 08, 2025 pm 06:03 PM
MySQLデータベースパフォーマンス最適化ガイドリソース集約型アプリケーションでは、MySQLデータベースが重要な役割を果たし、大規模なトランザクションの管理を担当しています。ただし、アプリケーションのスケールが拡大すると、データベースパフォーマンスのボトルネックが制約になることがよくあります。この記事では、一連の効果的なMySQLパフォーマンス最適化戦略を検討して、アプリケーションが高負荷の下で効率的で応答性の高いままであることを保証します。実際のケースを組み合わせて、インデックス作成、クエリ最適化、データベース設計、キャッシュなどの詳細な主要なテクノロジーを説明します。 1.データベースアーキテクチャの設計と最適化されたデータベースアーキテクチャは、MySQLパフォーマンスの最適化の基礎です。いくつかのコア原則は次のとおりです。適切なデータ型を選択し、ニーズを満たす最小のデータ型を選択すると、ストレージスペースを節約するだけでなく、データ処理速度を向上させることもできます。
 hadidb:pythonの軽量で水平方向にスケーラブルなデータベース
Apr 08, 2025 pm 06:12 PM
hadidb:pythonの軽量で水平方向にスケーラブルなデータベース
Apr 08, 2025 pm 06:12 PM
hadidb:軽量で高レベルのスケーラブルなPythonデータベースHadIDB(HadIDB)は、Pythonで記述された軽量データベースで、スケーラビリティが高くなっています。 PIPインストールを使用してHADIDBをインストールする:PIPINSTALLHADIDBユーザー管理CREATEユーザー:CREATEUSER()メソッド新しいユーザーを作成します。 Authentication()メソッドは、ユーザーのIDを認証します。 fromhadidb.operationimportuseruser_obj = user( "admin"、 "admin")user_obj。
 MySQLワークベンチはMariadBに接続できますか
Apr 08, 2025 pm 02:33 PM
MySQLワークベンチはMariadBに接続できますか
Apr 08, 2025 pm 02:33 PM
MySQLワークベンチは、構成が正しい場合、MariadBに接続できます。最初にコネクタタイプとして「mariadb」を選択します。接続構成では、ホスト、ポート、ユーザー、パスワード、およびデータベースを正しく設定します。接続をテストするときは、ユーザー名とパスワードが正しいかどうか、ポート番号が正しいかどうか、ファイアウォールが接続を許可するかどうか、データベースが存在するかどうか、MariadBサービスが開始されていることを確認してください。高度な使用法では、接続プーリングテクノロジーを使用してパフォーマンスを最適化します。一般的なエラーには、不十分な権限、ネットワーク接続の問題などが含まれます。エラーをデバッグするときは、エラー情報を慎重に分析し、デバッグツールを使用します。ネットワーク構成を最適化すると、パフォーマンスが向上する可能性があります
 MySQLにはサーバーが必要ですか
Apr 08, 2025 pm 02:12 PM
MySQLにはサーバーが必要ですか
Apr 08, 2025 pm 02:12 PM
生産環境の場合、パフォーマンス、信頼性、セキュリティ、スケーラビリティなどの理由により、通常、MySQLを実行するためにサーバーが必要です。サーバーには通常、より強力なハードウェア、冗長構成、より厳しいセキュリティ対策があります。小規模で低負荷のアプリケーションの場合、MySQLはローカルマシンで実行できますが、リソースの消費、セキュリティリスク、メンテナンスコストを慎重に考慮する必要があります。信頼性とセキュリティを高めるには、MySQLをクラウドまたは他のサーバーに展開する必要があります。適切なサーバー構成を選択するには、アプリケーションの負荷とデータボリュームに基づいて評価が必要です。




