モンテカルロ法で定積分を計算するPythonプログラミングを詳しく解説

この記事では主に Python プログラミングにおける定積分計算の詳細な説明を紹介します。必要な方は参考にしてください。

大学院受験の時、定積分の計算というこんな良いものがあると知りたかったのを思い出します。 。 。冗談ですが、当時は定積分の計算はそれほど簡単ではありませんでした。しかし、プログラミング言語を使用してより複雑な数学的問題を解決するというアイデアが私に生まれました。本題に入りましょう。

上図のように、区間[a b]上のf(x)の積分を計算すると、曲線とX軸で囲まれた赤い領域の面積を求めることになります。以下では、モンテカルロ法を使用して区間 [2 3] の定積分を計算します。 > モンテカルロ推定= 11.8181144118 正確な数値= 11.8113589251

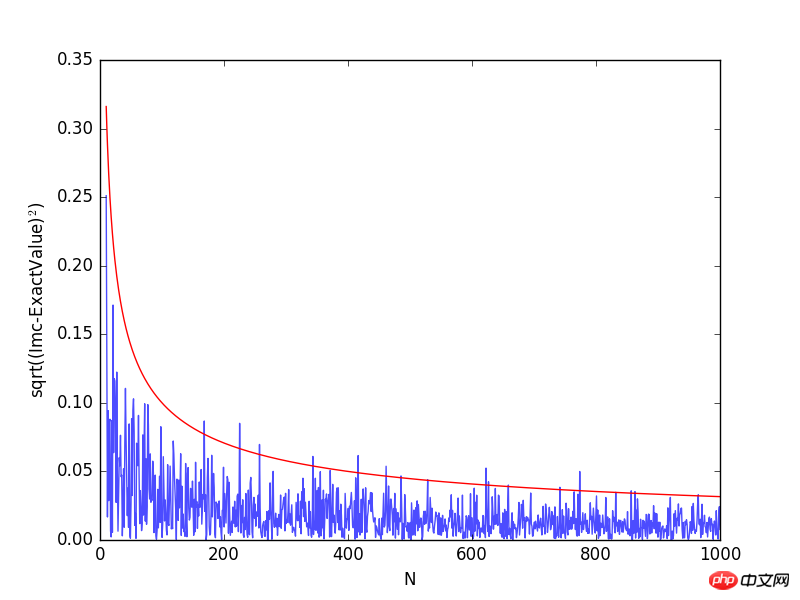
上図から分かるように、サンプリング点の数が増加するにつれて、計算誤差は徐々に減少します。シミュレーション結果の精度を向上させるには 2 つの方法があります。1 つはテスト数 N を増やすこと、もう 1 つは分散 σ2 を減らすことです。テスト数を増やすと、問題を解くために使用される合計コンピューター時間が必然的に増加します。精度向上のため、明らかに不適切な目的です。次に、分散を減らし、積分計算の精度を向上させるために重要なサンプリング方法を紹介します。

重要度サンプリング法の特徴は、特定のプロセスの確率分布からサンプリングするのではなく、修正された確率分布からサンプリングすることで、シミュレーション結果にとって重要なイベントがより多く現れることで、サンプリング効率が向上し、シミュレーション結果にとって重要ではないイベントに費やされる計算時間を削減します。たとえば、区間 [a b] 上の g(x) の積分を求めます。一様サンプリングを使用すると、関数値 g(x) が比較的小さい区間に生成されるサンプリング点の数と同じになります。関数値が大きい区間で生成されるサンプリング点の数を増やすと、明らかにサンプリング効率が高くなくなります。そのため、f(x) と g( x) は類似しており、これにより、積分計算に大きく寄与するサンプリング値が出現する確率が、寄与が小さいサンプリング値よりも大きくなることが保証されます。つまり、積分演算は次のように書き換えることができます。

x は確率密度 f(x) に従ってサンプリングによって得られる確率変数です。明らかに、区間 [a b] 内には次の値が存在するはずです。 したがって、整数値 I は容易に期待値と見なすことができます。確率変数 Y = g(x)/f(x) の、xi は確率密度 f(x) に従うサンプリング点です

次の例 正規分布関数 f(x) を使用して g を近似します(x)=sin(x)*x、正規分布に従ってサンプル値を選択し、区間[0 pi]上の整数∫g(x)dx

を計算します

# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt

def f(x):
  return x**2 + 4*x*np.sin(x) 
def intf(x): 
  return x**3/3.0+4.0*np.sin(x) - 4.0*x*np.cos(x)
a = 2;  
b = 3; 
# use N draws 
N= 10000
X = np.random.uniform(low=a, high=b, size=N) # N values uniformly drawn from a to b 
Y =f(X)  # CALCULATE THE f(x) 
# 蒙特卡洛法计算定积分：面积=宽度*平均高度
Imc= (b-a) * np.sum(Y)/ N;
exactval=intf(b)-intf(a)
print "Monte Carlo estimation=",Imc, "Exact number=", intf(b)-intf(a)
# --How does the accuracy depends on the number of points(samples)? Lets try the same 1-D integral 
# The Monte Carlo methods yield approximate answers whose accuracy depends on the number of draws.
Imc=np.zeros(1000)
Na = np.linspace(0,1000,1000)
exactval= intf(b)-intf(a)
for N in np.arange(0,1000):
  X = np.random.uniform(low=a, high=b, size=N) # N values uniformly drawn from a to b 
  Y =f(X)  # CALCULATE THE f(x) 
  Imc[N]= (b-a) * np.sum(Y)/ N;   
plt.plot(Na[10:],np.sqrt((Imc[10:]-exactval)**2), alpha=0.7)
plt.plot(Na[10:], 1/np.sqrt(Na[10:]), 'r')
plt.xlabel("N")
plt.ylabel("sqrt((Imc-ExactValue)$^2$)")
plt.show()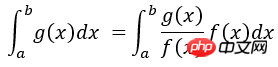

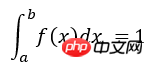図からわかるように、曲線sin(x)*xの形状は正規分布曲線の形状に似ているため、曲線のピークにおけるサンプリング点の数は位置よりも低くなります。カーブではもっとスペースが必要です。正確な計算の結果は pi です。上の右の図からわかるように、両方の方法で定積分が 1000 回計算され、正確な値 pi=3.1415 に近づくほど、正確な値から遠ざかります。明らかに、これは従来と一致しています。ただし、従来の手法を使用して計算された積分値の二乗の差 (赤色のヒストグラム) は、重要なサンプリング手法を使用した場合 (青色のヒストグラム) に比べて大幅に大きくなります。したがって、重要度サンプリング法を使用すると、分散を削減し、精度を向上させることができます。さらに、関数 f(x) の選択が計算結果の精度に影響することに注意してください。選択した関数 f(x) が g(x) と大きく異なる場合、計算結果の分散が大きくなります。も増えます。

関連する推奨事項:

Python プログラミングで NotImplementedError を使用する方法_python

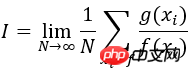
以上がモンテカルロ法で定積分を計算するPythonプログラミングを詳しく解説の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。