
この記事では、主に TensorFlow を使用してデミング回帰アルゴリズムを実装する例を紹介します。これには、必要な友人が参照できるように共有します。垂直距離の回帰直線 (つまり、y 軸方向に平行) を計算すると、デミング回帰は回帰直線 (つまり、回帰直線に垂直な距離) までの合計距離を最小化します。 x値とy値の両方向の誤差を最小化します。 具体的な比較表は以下のとおりです。
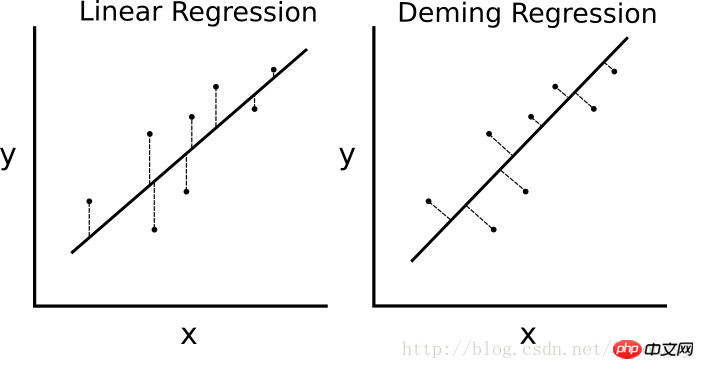
線形回帰アルゴリズムとデミング回帰アルゴリズムの違い。左側の線形回帰は回帰直線までの垂直距離を最小化し、右側のデミング回帰は回帰直線までの合計距離を最小化します。
線形回帰アルゴリズムの損失関数は垂直距離を最小化します。ここでは合計距離を最小化する必要があります。直線の傾きと切片を考慮すると、点から直線までの垂直距離を解く既知の幾何学的公式があります。幾何学式を入力して、TensorFlow に距離を最小化させます。
損失関数は、分子と分母から構成される幾何学的公式です。直線 y=mx+b と点 (x0, y0) が与えられた場合、その 2 つの間の距離を求める公式は次のとおりです。
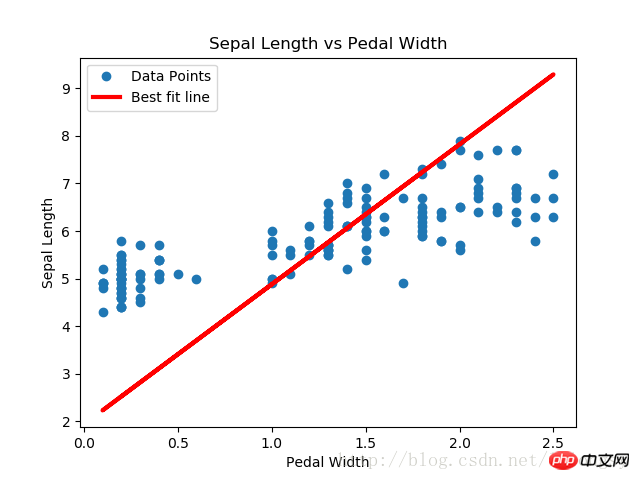
この記事 デミング回帰アルゴリズムと線形回帰アルゴリズムで得られる結果は基本的に同じです。 2 つの主な違いは、予測値とデータ ポイントの間の損失関数の測定です。線形回帰アルゴリズムの損失関数は垂直方向の距離の損失ですが、デミング回帰アルゴリズムは垂直方向の距離の損失 (距離の合計) です。 x 軸と y 軸)距離損失)。 ここでのデミング回帰アルゴリズムの実装タイプは全体回帰 (総最小二乗誤差) であることに注意してください。全体的な回帰アルゴリズムは、x 値と y 値の誤差が類似していることを前提としています。また、さまざまな誤差を使用して、さまざまな概念に従って x 軸と y 軸の間の距離の計算を拡張することもできます。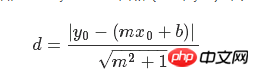 関連する推奨事項:
関連する推奨事項:
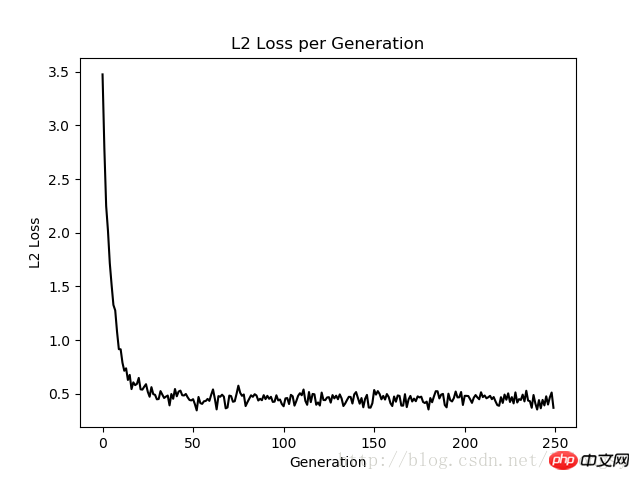
以上がTensorFlow を使用したデミング回帰アルゴリズムの実装例の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。