
今回は、PHP で多変量線形回帰シミュレーション曲線アルゴリズムを実装する手順について詳しく説明します。PHP で多変量線形回帰シミュレーション曲線アルゴリズムを実装するときに注意すべき注意事項は何ですか。実際のケースですので見てみましょう。
重線形回帰モデル:y = b1x1 + b2x2 + b3x3 +... +bnxn;
一連のデータに基づいています: 同様のarr_x = [[1, 2, 3, 4, 5] , [6, 7, 8, 9, 10], [11, 12, 13, 14, 15]]; arr_y = [5, 10, 15]; 最終的に取得したいのは、値を含む配列です。 b1 から bn まで;
方法: 最小二乗法を使用します数式:数式の前半のみを使用します。つまり、行列を使用して計算します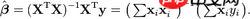
two-次元配列これは行列であり、式の y は arr_y と考えることができますが、行列 (5, 10, 15) とみなすこともできますが、縦方向に記述する必要があります。
その後、式によれば、行列の乗算、転置、反転を使用する必要があることがわかります。そのため、次のコードが 1 つずつ与えられます:public function get_complement($data, $i, $j) {
/* x和y为矩阵data的行数和列数 */
$x = count($data);
$y = count($data[0]);
/* data2为所求剩余矩阵 */
$data2 =[];
for ($k = 0; $k < $x -1; $k++) {
if ($k < $i) {
for ($kk = 0; $kk < $y -1; $kk++) {
if ($kk < $j) {
$data2[$k][$kk] = $data[$k][$kk];
} else {
$data2[$k][$kk] = $data[$k][$kk +1];
}
}
} else {
for ($kk = 0; $kk < $y -1; $kk++) {
if ($kk < $j) {
$data2[$k][$kk] = $data[$k +1][$kk];
} else {
$data2[$k][$kk] = $data[$k +1][$kk +1];
}
}
}
}
return $data2;
}
/* 计算矩阵行列式 */
public function cal_det($data) {
$ans = 0;
if (count($data[0]) === 2) {
$ans = $data[0][0] * $data[1][1] - $data[0][1] * $data[1][0];
} else {
for ($i = 0; $i < count($data[0]); $i++) {
$data_temp = $this->get_complement($data, 0, $i);
if ($i % 2 === 0) {
$ans = $ans + $data[0][$i] * ($this->cal_det($data_temp));
} else {
$ans = $ans - $data[0][$i] * ($this->cal_det($data_temp));
}
}
}
return $ans;
}
/*计算矩阵的伴随矩阵*/
public function ajoint($data) {
$m = count($data);
$n = count($data[0]);
$data2 =[];
for ($i = 0; $i < $m; $i++) {
for ($j = 0; $j < $n; $j++) {
if (($i + $j) % 2 === 0) {
$data2[$i][$j] = $this->cal_det($this->get_complement($data, $i, $j));
} else {
$data2[$i][$j] = - $this->cal_det($this->get_complement($data, $i, $j));
}
}
}
return $this->trans($data2);
}
/*转置矩阵*/
public function trans($data) {
$i = count($data);
$j = count($data[0]);
$data2 =[];
for ($k2 = 0; $k2 < $j; $k2++) {
for ($k1 = 0; $k1 < $i; $k1++) {
$data2[$k2][$k1] = $data[$k1][$k2];
}
}
/*将矩阵转置便可得到伴随矩阵*/
return $data2;
}
/*求矩阵的逆,输入参数为原矩阵*/
public function inv($data) {
$m = count($data);
$n = count($data[0]);
$data2 =[];
$det_val = $this->cal_det($data);
$data2 = $this->ajoint($data);
for ($i = 0; $i < $m; $i++) {
for ($j = 0; $j < $n; $j++) {
$data2[$i][$j] = $data2[$i][$j] / $det_val;
}
}
return $data2;
}
/*求两矩阵的乘积*/
public function getProduct($data1, $data2) {
/*$data1 为左乘矩阵*/
$m1 = count($data1);
$n1 = count($data1[0]);
$m2 = count($data2);
$n2 = count($data2[0]);
$data_new =[];
if ($n1 !== $m2) {
return false;
} else {
for ($i = 0; $i <= $m1 -1; $i++) {
for ($k = 0; $k <= $n2 -1; $k++) {
$data_new[$i][$k] = 0;
for ($j = 0; $j <= $n1 -1; $j++) {
$data_new[$i][$k] += $data1[$i][$j] * $data2[$j][$k];
}
}
}
}
return $data_new;
}
/*多元线性方程*/
public function getParams($arr_x, $arr_y) {
$final =[];
$arr_x_t = $this->trans($arr_x);
$result = $this->getProduct($this->getProduct($this->inv($this->getProduct($arr_x_t, $arr_x)), $arr_x_t), $arr_y);
foreach ($result as $key => $val) {
foreach ($val as $_k => $_v) {
$final[] = $_v;
}
}
return $final;
} メソッドは、b パラメーター配列を見つけるための最後のメソッドです。 pass in 2 次元配列 arr_x とgetParams()1 次元配列arr_y で十分です。
PHP で foreach を使用して配列を変換する手順の詳細な説明
php 1 次元配列の value 要素を削除する手順の詳細な説明
以上がPHP で重回帰シミュレーション曲線アルゴリズムを実装する手順の詳細な説明の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。