
この記事では主に、PHP を使用してバイナリ ヒープを使用して TopK アルゴリズムを実装する方法を紹介します。記事内の紹介は非常に詳細であり、必要な場合はエディターに従って学習することができます。一緒に。
前書き
私は過去に仕事や面接をしているときによく問題に遭遇しました。大規模な TopN を達成する方法は、非常に大きな結果セットの中から最大の上位 10 位または上位 100 位の数字を素早く見つけることです。メモリと速度の効率を確保するために、最初のアイデアはソートを使用し、上位 10 または 100 を横取りすることです。量が特に大きくない場合はソートは問題ありませんが、量が非常に多い場合はソートが問題になります。たとえば、配列またはテキスト ファイルに数億の数値がある場合、それらをすべてメモリに読み取ることは不可能であるため、この問題を解決するために並べ替えを使用するのは最善ではありません。 PHP を使用して小さなトップ ヒープを実装します
バイナリ ヒープ
バイナリ ヒープは、完全なバイナリ ツリーまたはほぼ完全なバイナリ ツリーの 2 つのタイプがあります。バイナリ ヒープ、最大ヒープ、最小ヒープの値。最大ヒープ: 親ノードのキー値は常に子ノードのキー値以上です。最小ヒープ: 親ノードのキー値は常に小さいです。または子ノードのキー値と等しい

小丁ヒープ - (インターネットからの画像)
バイナリ ヒープは通常、配列で表されます (たとえば、ルートの位置を参照)。配列内のノードは 0 で、n 番目の位置の子ノードはそれぞれ 2n+1 と 2n +2 にあります。したがって、位置 0 の子ノードは 1 と 2 にあり、1 の子ノードは 3 と 2n にあります。 4 など。この保存方法により、親ノードと子ノードを見つけやすくなります。
ここでは、具体的な概念的問題については詳しく説明しません。バイナリ ヒープについて質問がある場合は、このデータ構造をよく理解してください。次に、PHP コードを使用して上記の topN を実装し、解決します。違いを確認するには、ここで並べ替えメソッドを使用して実装し、それがどのように機能するかを確認します。
クイックソートアルゴリズムを使用してTopNを実装します
//为了测试运行内存调大一点
ini_set('memory_limit', '2024M');
//实现一个快速排序函数
function quick_sort(array $array){
$length = count($array);
$left_array = array();
$right_array = array();
if($length <= 1){
return $array;
}
$key = $array[0];
for($i=1;$i<$length;$i++){
if($array[$i] > $key){
$right_array[] = $array[$i];
}else{
$left_array[] = $array[$i];
}
}
$left_array = quick_sort($left_array);
$right_array = quick_sort($right_array);
return array_merge($right_array,array($key),$left_array);
}
//构造500w不重复数
for($i=0;$i<5000000;$i++){
$numArr[] = $i;
}
//打乱它们
shuffle($numArr);
//现在我们从里面找到top10最大的数
var_dump(time());
print_r(array_slice(quick_sort($all),0,10));
var_dump(time());
実行後の結果
上位10の結果が上に表示され、実行時間が出力されていることがわかります、約 99 秒ですが、これは 500 万の数値をメモリにロードできる場合に限ります。5kw または 5 億の数値を含むファイルがある場合、
バイナリ ヒープ アルゴリズムを使用すると、必ず問題が発生します。 TopN
の実装プロセスは次のとおりです:
1. 最初に 10 または 100 の数値を配列に読み取ります。これが TopN の数値です
2. 小さな頂点を生成する関数を呼び出します。このとき、ヒープの先頭が最小である必要があります。 3. ファイルまたは配列の残りの数値をすべて順にスキャンします。サイズを比較し、ヒープの最上位の要素より小さい場合は破棄し、ヒープの最上位の要素より大きい場合は置き換えます。
5. ヒープの最上位要素を置き換えた後、小さな最上位ヒープを生成する関数を呼び出して、再度見つける必要があるため、最小の最上位ヒープを生成します
6上記の 4 ~ 5 の手順を繰り返し、すべての走査が完了すると、小さなトップ ヒープは常に最小のヒープと速度を除外するため、小さなトップ ヒープ内の最大の topN が最大になります。小さな上部ヒープの調整も非常に高速です。相対的な調整を行って、ルート ノードが左右のノードよりも小さくなるようにします
7. アルゴリズムの複雑さに関しては、最悪の場合でもトップ 10 に準拠しています。この場合、1 つをトラバースすることになります。数値をヒープの先頭に置き換えると、10 回調整する必要があり、ソートよりも高速であり、すべての内容がメモリに読み込まれるわけではないことがわかります。達成は線形トラバーサルです。
//生成小顶堆函数
function Heap(&$arr,$idx){
$left = ($idx << 1) + 1;
$right = ($idx << 1) + 2;
if (!$arr[$left]){
return;
}
if($arr[$right] && $arr[$right] < $arr[$left]){
$l = $right;
}else{
$l = $left;
}
if ($arr[$idx] > $arr[$l]){
$tmp = $arr[$idx];
$arr[$idx] = $arr[$l];
$arr[$l] = $tmp;
Heap($arr,$l);
}
}
//这里为了保证跟上面一致,也构造500w不重复数
/*
当然这个数据集并不一定全放在内存,也可以在
文件里面,因为我们并不是全部加载到内存去进
行排序
*/
for($i=0;$i<5000000;$i++){
$numArr[] = $i;
}
//打乱它们
shuffle($numArr);
//先取出10个到数组
$topArr = array_slice($numArr,0,10);
//获取最后一个有子节点的索引位置
//因为在构造小顶堆的时候是从最后一个有左或右节点的位置
//开始从下往上不断的进行移动构造(具体可看上面的图去理解)
$idx = floor(count($topArr) / 2) - 1;
//生成小顶堆
for($i=$idx;$i>=0;$i--){
Heap($topArr,$i);
}
var_dump(time());
//这里可以看到,就是开始遍历剩下的所有元素
for($i = count($topArr); $i < count($numArr); $i++){
//每遍历一个则跟堆顶元素进行比较大小
if ($numArr[$i] > $topArr[0]){
//如果大于堆顶元素则替换
$topArr[0] = $numArr[$i];
/*
重新调用生成小顶堆函数进行维护,只不过这次是从堆顶
的索引位置开始自上往下进行维护,因为我们只是把堆顶
的元素给替换掉了而其余的还是按照根节点小于左右节点
的顺序摆放这也就是我们上面说的,只是相对调整下,并
不是全部调整一遍
*/
Heap($topArr,0);
}
}
var_dump(time());
最終結果もトップ10であることがわかりますが、所要時間はわずか1秒程度で、メモリと時間効率の両方を満たしています並べ替えの最も良い点は、並べ替える必要がないため、すべてのデータ セットをメモリに読み込む必要がないことです。上記はデモンストレーション用であるため、500 万の要素がメモリ内に直接構築されます。ただし、データ構造の核心は線形トラバーサルをメモリ内の非常に小さな最上位ヒープ構造と比較し、最終的に TopN を取得することであるため、これらすべてをファイルに転送し、1 行ずつ読み取り、比較することができます。 .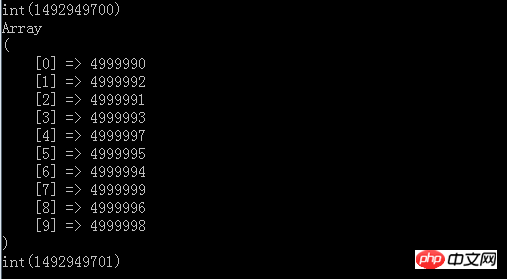
以上がこの記事の全内容です、皆様の学習のお役に立てれば幸いです。
関連する推奨事項: 16 進数変換を実現するための
Linux で redis と phpredis をコンパイルする方法_php のヒント
PHPMysqli クラス ライブラリを使用してページネーションのメソッドeffect_phpスキル
以上がPHP はバイナリ ヒープを使用して TopK アルゴリズムを実装しますの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。