キャンバス内のランダムな点に基づいて多角形を描画する方法
この記事は主に、キャンバス内のランダムな点に基づいてポリゴンを描画する方法に関する関連情報を紹介します。内容は非常に優れているので、参考として共有します。
原因
今日、「HTML5+Javascriptアニメーションの基礎」という本を勉強していたとき、第8章の3番目のセクションで、3本のバネを使って3点を結び、ストレッチ動作を実行する方法について話しました。
例を終えた後、4点や5点だったらどうなるかを考えました。
コードを書き直してポイント数を可変にしました。最終的な効果は、バランスをとるために各ポイントの最終的なストレッチ動作を実現することですが、ポイント間の接続はあまり見栄えがよくなく、いくつかは交差しています。
そこで、この領域を最適化できないか考えました。
接続を回転させます
前の例の点はすべてランダムな位置にあるため、接続は制御できません。ということで、まずはこれから始めたいと思います。
まず、ある点を基準点として使用し、この点に対する他の点の角度を取得します。
次に、これらの点を小さい角度から大きい角度まで角度に応じて接続すると、正多角形を描くことができます。
おおよその実装コードは以下の通りです:
let balls = [];
let ballNum = 6;
let firstBall = null;
while(ballNum--) {
let ball = new Ball(20, parseColor(Math.random() * 0xffffff))
ball.x = Math.random() * width;
ball.y = Math.random() * height;
balls.push(ball)
if (!firstBall) {
firstBall = ball
ball.angle = 0
} else {
const dx = ball.x - firstBall.x,
dy = ball.y - firstBall.y;
ball.angle = Math.atan2(dy, dx);
}
}
// 尝试让球连线是一个正多边形
balls = balls.sort((ballA, ballB) => {
return ballA.angle - ballB.angle
})このようにして、最後に接続を描画する際に、配列を横断して小さい角度から大きい角度まで描画することができます。
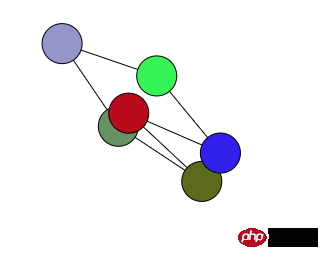
その効果は次のとおりです:

これにより、一線を越える状況を大幅に減らすことができますが、それでも完全に回避することはできません。
次に、Math.abs を使用して正の角度にするか、各点を結ぶ最小角度の点を見つけるなど、このソリューションの最適化を試みたいと思います。しかし結果はダメ、一線越えは避けられない。
中心点に基づいて回転
後で別のアイデアが思いつきました。多角形の中心点が決定できれば、中心点に対するすべての点の角度を個別に計算できます。ポイントは時計回りまたは反時計回りに接続できます。
しかし、インターネットで長時間検索した結果、すべての点アルゴリズムには特定の時計回りの順序で配置された一連の点が必要であることがわかりました。
でも、これらのポイントがあれば、すでに多角形を描くことができます。諦めざるを得ませんでした
X 軸極セグメンテーション
絶望のあまり、Google で検索しなければならなかったのですが、Zhihu で良い答えを見つけました: How to connect an unordered set of points on the plan into aシンプルなポリゴン?
具体的なアルゴリズムの説明については、答えを見てください。詳細には触れません。
ただし、上のチェーンと下のチェーンを接続する際は、実際には上のチェーンがX軸の降順に接続され、下のチェーンがX軸の昇順に接続されるようにするだけで済みます(反時計回りに描かれます)。 X 軸が同じ点については、Y 軸が大きいか小さいかは関係ありません。
実装される場合は、回答のアルゴリズムに従って厳密に実装されます。
点が上のチェーンに属するか、下のチェーンに属するかを判断するとき、最初に考えるべきことは、2つの点に基づいて直線の関数方程式を決定し、次に計算する点の座標を導入することです。しかし後になって、すべての点が左端の極を使用して斜角を計算し、それを角度の大きさに応じて分割するほうが視覚的に理解しやすいと思いました。
おおよそのコードは次のとおりです:
let balls = [];
let tempBalls = [];
let ballNum = 6;
let isDragingBall = false;
while(ballNum--) {
let ball = new Ball(10, parseColor(Math.random() * 0xffffff))
ball.x = Math.random() * width;
ball.y = Math.random() * height;
tempBalls.push(ball)
}
// 让点按X轴升序排序
tempBalls = tempBalls.sort((ballA, ballB) => {
return ballA.x - ballB.x
})
// 找X轴左右极点
let firstBall = tempBalls[0],
lastBall = tempBalls[tempBalls.length -1];
let smallXBalls = tempBalls.filter(ball => ball.x === firstBall.x),
bigXBalls = tempBalls.filter(ball => ball.x === lastBall.x)
// 处理左右极点有多个的情况
if (smallXBalls.length > 1) {
smallXBalls.sort((ballA, ballB) => {
return ballB.y - ballA.y
})
}
if (bigXBalls.length > 1) {
bigXBalls.sort((ballA, ballB) => {
return ballB.y - ballA.y
})
}
firstBall = smallXBalls[0]
lastBall = bigXBalls[0]
// 获得极点连线的角度
let splitLineAngle = Math.atan2(lastBall.y - firstBall.y, lastBall.x - firstBall.x);
let upperBalls = [],
lowerBalls = [];
// 所有其他点跟firstBall计算角度
// 大于splitLineAngle的都是下链
// 其他是上链
tempBalls.forEach(ball => {
if (ball === firstBall || ball === lastBall) {
return false
}
let angle = Math.atan2(ball.y - firstBall.y, ball.x - firstBall.x);
if (angle > splitLineAngle) {
lowerBalls.push(ball)
} else {
upperBalls.push(ball)
}
})
// 处理X轴相同情况的排序
lowerBalls = lowerBalls.sort((ballA, ballB) => {
if (ballA.x !== ballB.x) {
return ballA.x - ballB.x
}
return ballB.y - ballA.y
})
upperBalls = upperBalls.sort((ballA, ballB) => {
if (ballA.x !== ballB.x) {
return ballB.x - ballA.x
}
return ballB.y - ballB.x
})
// 逆时针连接所有的点
balls = [firstBall].concat(lowerBalls, [lastBall], upperBalls)
balls = balls.map((ball, i) => {
ball.text = i + 1;
return ball
})最終的に返されるボールは、反時計回りにソートされた多角形の点です。
効果は次のとおりです:
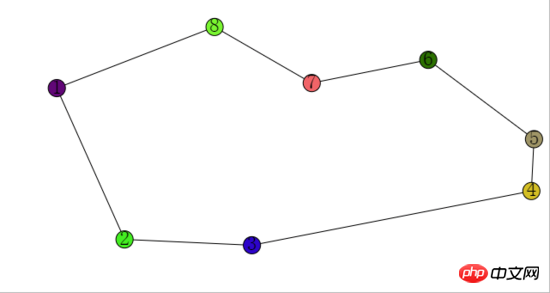
各ボールの内部ステータスは次のとおりです:

以上がこの記事の全内容であり、皆様の学習に役立つことを願っています。関連コンテンツについては、PHP 中国語 Web サイトにご注意ください。
関連する推奨事項:
html5 を使用する
Canvas は、echarts では実装できない円グラフをカプセル化します
HTML5 Canvas は、曲線を描画するメソッドを実装します
以上がキャンバス内のランダムな点に基づいて多角形を描画する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7752
7752
 15
15
 1643
1643
 14
14
 1398
1398
 52
52
 1293
1293
 25
25
 1234
1234
 29
29
 間取り図を建築pptに直接描くことはできますか?
Mar 20, 2024 am 08:43 AM
間取り図を建築pptに直接描くことはできますか?
Mar 20, 2024 am 08:43 AM
pptは、特に教育、建築など、多くの分野や仕事で広く使用されています。建築pptに関しては、まず建築図面のプレゼンテーションを考えなければなりませんが、専門的な図面ソフトウェアを使用しない場合、簡単な建築図面を直接描くことはできますか?実際には、ここで作業は完了します。以下に、アイデアを提供するために、比較的簡単な平面図を描きます。このアイデアに基づいて、より良い平面図を完成させることができれば幸いです。 1. まず、デスクトップ上で ppt ソフトウェアをダブルクリックして開き、新しいプレゼンテーションの空のドキュメントをクリックして作成します。 2. メニューバーに「挿入」→「図形」→「四角形」があります。 3. 長方形を描画した後、グラフィックをダブルクリックし、塗りつぶしの色のタイプを変更します。
 七角形数
Sep 24, 2023 am 10:33 AM
七角形数
Sep 24, 2023 am 10:33 AM
七角形の数は、七角形として表現できる数です。七角形は、7つの辺を持つ多角形です。七角形の数は、七角形(7角形)の連続した層の組み合わせで表現できます。七角形の数は、下の図でよりよく説明できます。したがって、
 キャンバス フレームワークを学び、一般的に使用されるキャンバス フレームワークについて詳しく説明します
Jan 17, 2024 am 11:03 AM
キャンバス フレームワークを学び、一般的に使用されるキャンバス フレームワークについて詳しく説明します
Jan 17, 2024 am 11:03 AM
Canvas フレームワークを探索する: 一般的に使用される Canvas フレームワークを理解するには、特定のコード例が必要です。 はじめに: Canvas は HTML5 で提供される描画 API であり、これを通じて豊富なグラフィックスやアニメーション効果を実現できます。描画の効率と利便性を向上させるために、多くの開発者がさまざまな Canvas フレームワークを開発しました。この記事では、一般的に使用される Canvas フレームワークをいくつか紹介し、読者がこれらのフレームワークの使用方法をより深く理解できるように、具体的なコード例を示します。 1.EaselJSフレームワークEa
 5 分で Python で樹状図とレーダー チャートを描画する方法を学びます
Sep 27, 2023 pm 12:48 PM
5 分で Python で樹状図とレーダー チャートを描画する方法を学びます
Sep 27, 2023 pm 12:48 PM
5 分で Python を使用してデンドログラムとレーダー チャートを描画する方法を学びましょう。データ視覚化では、デンドログラムとレーダー チャートは一般的に使用される 2 つのチャート形式です。ツリーマップは階層構造を表示するために使用され、レーダー チャートは複数の次元にわたるデータを比較するために使用されます。この記事では、Python を使用してこれら 2 つのグラフを描画する方法と、具体的なコード例を紹介します。 1. 樹状図の描画 Python には、matplotlib やgraphviz など、樹状図の描画に使用できるライブラリが複数あります。以下では、例として matplotlib ライブラリを使用して説明します。
 Python で 3D 地理グラフを描画する方法
Sep 28, 2023 am 10:19 AM
Python で 3D 地理グラフを描画する方法
Sep 28, 2023 am 10:19 AM
Python で 3D 地理グラフを描画する方法の概要: 3D 地理グラフを描画すると、地理データと空間分布をより直観的に理解するのに役立ちます。 Python は強力で使いやすいプログラミング言語として、さまざまな種類の地理図を描画するためのライブラリとツールを多数提供しています。この記事では、Python プログラミング言語と、Matplotlib や Basemap などのいくつかの人気のあるライブラリを使用して 3D 地理グラフを描画する方法を学びます。環境の準備: 開始する前に、次のことを確認する必要があります。
 html2canvas にはどのようなバージョンがありますか?
Aug 22, 2023 pm 05:58 PM
html2canvas にはどのようなバージョンがありますか?
Aug 22, 2023 pm 05:58 PM
html2canvas のバージョンには、html2canvas v0.x、html2canvas v1.x などが含まれます。詳細な紹介: 1. html2canvas v0.x (html2canvas の初期バージョン) 最新の安定バージョンは v0.5.0-alpha1 です。これは、多くのプロジェクトで広く使用され、検証されている成熟したバージョンです。2. html2canvas v1.x、これは html2canvas の新しいバージョンです。
 uniapp は、キャンバスを使用してチャートやアニメーション効果を描画する方法を実装します。
Oct 18, 2023 am 10:42 AM
uniapp は、キャンバスを使用してチャートやアニメーション効果を描画する方法を実装します。
Oct 18, 2023 am 10:42 AM
キャンバスを使用して uniapp でチャートやアニメーション効果を描画する方法には、特定のコード例が必要です。 1. はじめに モバイル デバイスの普及に伴い、モバイル端末上でさまざまなチャートやアニメーション効果を表示する必要があるアプリケーションがますます増えています。 uniapp は、Vue.js に基づくクロスプラットフォーム開発フレームワークとして、キャンバスを使用してチャートやアニメーション効果を描画する機能を提供します。この記事では、uniapp がキャンバスを使用してチャートやアニメーション効果を実現する方法を紹介し、具体的なコード例を示します。 2.キャンバス
 Python でアニメーション チャートを描画する方法
Sep 27, 2023 am 09:53 AM
Python でアニメーション チャートを描画する方法
Sep 27, 2023 am 09:53 AM
Python でアニメーション チャートを描画する方法 Python は強力なプログラミング言語として、さまざまなデータの視覚化やチャートの描画に使用できます。中でも、アニメーション チャートを描画すると、データをより鮮明で興味深いものにすることができます。この記事では、Python を使用してアニメーション チャートを描画する方法と、具体的なコード例を紹介します。まず、Python で最も一般的に使用されるグラフ作成ライブラリの 1 つである matplotlib ライブラリをインストールする必要があります。ターミナルで次のコマンドを実行して matplotlib をインストールします: pipinsta




