 再帰は、より複雑な問題に対処するために使用されます。すべての問題が反復だけで解決できるわけではありません。再帰では関数呼び出しを使用して呼び出しスタックを管理するため、反復よりも多くの時間とメモリを使用します。さらに、反復では、各ステップで結果が得られますが、再帰では、結果が得られる前に、基本ケースの実行が終了するまで待つ必要があります。上記の例を見ると、再帰的アルゴリズムでは結果を保存するための変数や宣言がありませんが、反復的アルゴリズムでは $result を使用して返された結果を毎回保存していることがわかります。
再帰は、より複雑な問題に対処するために使用されます。すべての問題が反復だけで解決できるわけではありません。再帰では関数呼び出しを使用して呼び出しスタックを管理するため、反復よりも多くの時間とメモリを使用します。さらに、反復では、各ステップで結果が得られますが、再帰では、結果が得られる前に、基本ケースの実行が終了するまで待つ必要があります。上記の例を見ると、再帰的アルゴリズムでは結果を保存するための変数や宣言がありませんが、反復的アルゴリズムでは $result を使用して返された結果を毎回保存していることがわかります。
PHPデータ構造に基づく再帰
この記事では主に PHP のデータ構造に基づいた再帰を紹介しますが、これは参考になるものです。今回はそれを共有します。必要な友人は参考にしてください。
再帰とは何ですか?
前に述べたように、再帰は大きな問題を小さな問題に分割する解決策です。一般に、再帰は関数自体の呼び出しと呼ばれます。このように言うと奇妙に聞こえるかもしれませんが、実際、再帰では関数はそれ自体を呼び出す必要があります。
A栗
たとえば、数学では、「階乗」という概念を誰もが知っています。たとえば、5 の階乗は 5*4*3*2*1 です。
- #5! = 5 * 4!
- 4! = 4 * 3!
- 3! = 3 * 2! #######2! = 2 * 1!
- 1! = 1 * 0! #0! = 1
- n の階乗を求めるルール、つまり n! = n * (n -1) !
これは再帰を反映しています。このことから、5 の階乗を段階的に別の小さな問題に変換したことがわかります。
再帰アルゴリズムの特徴
すべての再帰呼び出しは、小さな副問題に基づいている必要があります。たとえば、5 の階乗は 5 に 4 を掛けた階乗です。
- 再帰には基本ケースが必要です。たとえば、階乗の基本ケースは 0 です。条件が 0 の場合、再帰は停止します。
- 再帰中のループ呼び出しは避けてください。そうしないと、コンピュータは最終的にスタック オーバーフロー エラーを表示します。
-
function factorial(int $n): int { if ($n = 0) { return 1; } return $n * factorial($n - 1); }ログイン後にコピー上記のコードを見ると、階乗問題を解決するための基本条件、つまり n が 0 の場合に 1 を返すことがわかります。この条件が満たされない場合は、 - n
に
factorial(n) を乗算した値が返されます。これは、再帰プロパティの最初と 3 番目の項目を満たします。各再帰呼び出しを大きな問題の小さなサブ問題に分割するため、ループ呼び出しを回避します。上記のアルゴリズムのアイデアは次のように表すことができます:
再帰と反復反復法を使用して上記の再帰コードを実装することもできます
function factorial(int $n): int
{
$result = 1;
for ($i = $n; $i > 0; $i--) {
$result*= $n;
}
return $result;
} 再帰は、より複雑な問題に対処するために使用されます。すべての問題が反復だけで解決できるわけではありません。再帰では関数呼び出しを使用して呼び出しスタックを管理するため、反復よりも多くの時間とメモリを使用します。さらに、反復では、各ステップで結果が得られますが、再帰では、結果が得られる前に、基本ケースの実行が終了するまで待つ必要があります。上記の例を見ると、再帰的アルゴリズムでは結果を保存するための変数や宣言がありませんが、反復的アルゴリズムでは $result を使用して返された結果を毎回保存していることがわかります。
再帰は、より複雑な問題に対処するために使用されます。すべての問題が反復だけで解決できるわけではありません。再帰では関数呼び出しを使用して呼び出しスタックを管理するため、反復よりも多くの時間とメモリを使用します。さらに、反復では、各ステップで結果が得られますが、再帰では、結果が得られる前に、基本ケースの実行が終了するまで待つ必要があります。上記の例を見ると、再帰的アルゴリズムでは結果を保存するための変数や宣言がありませんが、反復的アルゴリズムでは $result を使用して返された結果を毎回保存していることがわかります。
フィボナッチ数列
数学では、フィボナッチ数列は特別な整数列です。数列内の各数値は、他の 2 つの数値の合計によって生成されます。ルールは次のとおりです。
function fibonacci($n)
{
if ($n == 0) {
return 0;
}
if ($n == 1) {
return 1;
}
return fibonacci($n - 1) + fibonacci($ - 2);
}ログイン後にコピー
最大公約数再帰アルゴリズムを使用するもう 1 つの一般的な問題は、2 つの数値の最大公約数を見つけることです。 function fibonacci($n)
{
if ($n == 0) {
return 0;
}
if ($n == 1) {
return 1;
}
return fibonacci($n - 1) + fibonacci($ - 2);
}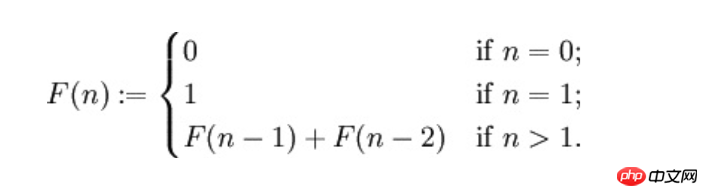
function gcd(int $a, int $b)
{
if ($b == 0) {
return $a;
}
return gcd($b, $a % $b);
}ログイン後にコピー再帰型
function gcd(int $a, int $b)
{
if ($b == 0) {
return $a;
}
return gcd($b, $a % $b);
}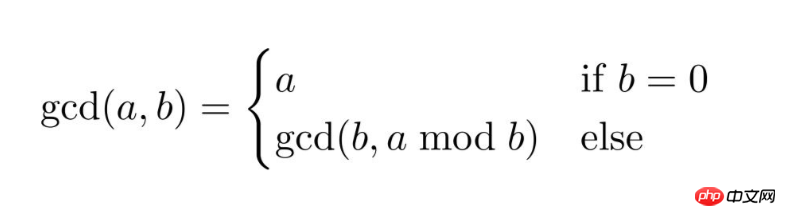 線形再帰
線形再帰
- すべての再帰呼び出しでは、関数は自分自身を 1 回だけ呼び出します。これを線形再帰と呼びます。
- 二項再帰
- 二項再帰では、関数への各再帰呼び出しがそれ自体を 2 回呼び出します。フィボナッチ数列を解くアルゴリズムは二分再帰であり、他にも二分探索、分割統治アルゴリズム、マージソートなども二分再帰を利用します。
- 末尾再帰
- 再帰が操作を待たずに戻る場合、それは末尾再帰と呼ばれます。フィボナッチアルゴリズムでは、戻り値に前回の再帰の戻り値を乗算する必要があるため、末尾再帰ではなく、最大公約数を解くアルゴリズムは末尾再帰です。末尾再帰は線形再帰の形式です。
- 相互再帰
- たとえば、各再帰呼び出しでは、A() は B() を呼び出し、B() は A() を呼び出します。このような再帰は相互再帰と呼ばれます。
- ネストされた再帰
- 再帰関数がそれ自体をパラメーターとして再帰的に呼び出す場合、それはネストされた再帰と呼ばれます。一般的な例はアッカーマン関数です。以下の式を参照してください。
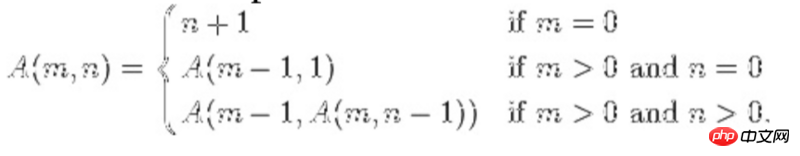 次の記事では、再帰を使用して、N レベル分類の構築、ネストされたコメントの構築、ディレクトリ ファイルの走査など、実際の開発で遭遇するいくつかの問題を解決します。
次の記事では、再帰を使用して、N レベル分類の構築、ネストされたコメントの構築、ディレクトリ ファイルの走査など、実際の開発で遭遇するいくつかの問題を解決します。
上記がこの記事の全内容です。皆様の学習に役立つことを願っています。その他の関連コンテンツについては、PHP 中国語 Web サイトに注目してください。
関連する推奨事項:
PHP でクライアントの実際の IP アドレスを取得する方法
PHP で Elasticsearch を使用する方法PHP
以上がPHPデータ構造に基づく再帰の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7663
7663
 15
15
 1393
1393
 52
52
 1205
1205
 24
24
 91
91
 11
11
 C++ 関数の再帰的実装: 再帰の深さに制限はありますか?
Apr 23, 2024 am 09:30 AM
C++ 関数の再帰的実装: 再帰の深さに制限はありますか?
Apr 23, 2024 am 09:30 AM
C++ 関数の再帰の深さは制限されており、この制限を超えるとスタック オーバーフロー エラーが発生します。制限値はシステムやコンパイラによって異なりますが、通常は 1,000 ~ 10,000 の間です。解決策には次のものが含まれます: 1. 末尾再帰の最適化、2. 末尾呼び出し、3. 反復実装。
 C++ ラムダ式は再帰をサポートしていますか?
Apr 17, 2024 pm 09:06 PM
C++ ラムダ式は再帰をサポートしていますか?
Apr 17, 2024 pm 09:06 PM
はい、C++ ラムダ式は std::function を使用して再帰をサポートできます。std::function を使用して Lambda 式への参照をキャプチャします。キャプチャされた参照を使用すると、ラムダ式はそれ自体を再帰的に呼び出すことができます。
 C++ 関数の再帰的実装: 再帰的アルゴリズムと非再帰的アルゴリズムの比較分析?
Apr 22, 2024 pm 03:18 PM
C++ 関数の再帰的実装: 再帰的アルゴリズムと非再帰的アルゴリズムの比較分析?
Apr 22, 2024 pm 03:18 PM
再帰アルゴリズムは、関数の自己呼び出しを通じて構造化された問題を解決します。利点は、シンプルで理解しやすいことですが、欠点は、効率が低く、スタック オーバーフローを引き起こす可能性があることです。非再帰アルゴリズムは、明示的に管理することで再帰を回避します。スタック データ構造の利点は、より効率的でスタックのオーバーフローを回避できることですが、欠点はコードがより複雑になる可能性があることです。再帰的か非再帰的かの選択は、問題と実装の特定の制約によって異なります。
 C++ で配列の最小要素と最大要素を見つける再帰的プログラム
Aug 31, 2023 pm 07:37 PM
C++ で配列の最小要素と最大要素を見つける再帰的プログラム
Aug 31, 2023 pm 07:37 PM
整数配列 Arr[] を入力として受け取ります。目標は、再帰的メソッドを使用して配列内の最大要素と最小要素を見つけることです。再帰を使用しているため、長さ = 1 に達するまで配列全体を反復処理し、基本ケースを形成する A[0] を返します。それ以外の場合、現在の要素は現在の最小値または最大値と比較され、その値は後続の要素に対して再帰的に更新されます。この場合のさまざまな入出力シナリオを見てみましょう −入力 −Arr={12,67,99,76,32}; 出力 −配列内の最大値: 99 説明 &mi
 Java で部分文字列の出現数を再帰的にカウントする
Sep 17, 2023 pm 07:49 PM
Java で部分文字列の出現数を再帰的にカウントする
Sep 17, 2023 pm 07:49 PM
2 つの文字列 str_1 と str_2 を指定します。目的は、再帰的プロシージャを使用して、文字列 str1 内の部分文字列 str2 の出現数をカウントすることです。再帰関数は、その定義内で自分自身を呼び出す関数です。 str1 が「Iknowthatyouknowthatiknow」、str2 が「know」の場合、出現回数は -3 になります。例を通して理解しましょう。たとえば、入力 str1="TPisTPareTPamTP"、str2="TP"; 出力 Countofoccurrencesofasubstringrecursi
 C++関数の再帰の詳しい解説:文字列処理における再帰の応用
Apr 30, 2024 am 10:30 AM
C++関数の再帰の詳しい解説:文字列処理における再帰の応用
Apr 30, 2024 am 10:30 AM
再帰関数は、文字列処理の問題を解決するためにそれ自体を繰り返し呼び出す手法です。無限再帰を防ぐために終了条件が必要です。再帰は、文字列の反転や回文チェックなどの操作で広く使用されています。
 C++ 再帰の上級: 末尾再帰の最適化とその応用について理解する
Apr 30, 2024 am 10:45 AM
C++ 再帰の上級: 末尾再帰の最適化とその応用について理解する
Apr 30, 2024 am 10:45 AM
末尾再帰最適化 (TRO) は、特定の再帰呼び出しの効率を向上させます。末尾再帰呼び出しをジャンプ命令に変換し、コンテキスト状態をスタックではなくレジスターに保存することで、余分な呼び出しとスタックへの戻り操作を排除し、アルゴリズムの効率を向上させます。 TRO を使用すると、末尾再帰関数 (階乗計算など) を最適化できます。末尾再帰呼び出しを goto ステートメントに置き換えることで、コンパイラーは goto ジャンプを TRO に変換し、再帰アルゴリズムの実行を最適化します。
 C++ 再帰の初心者ガイド: 基礎の構築と直感の開発
May 01, 2024 pm 05:36 PM
C++ 再帰の初心者ガイド: 基礎の構築と直感の開発
May 01, 2024 pm 05:36 PM
再帰は、問題を解決するために関数自体を呼び出すことを可能にする強力な手法です。C++ では、再帰関数は、基本ケース (再帰をいつ停止するかを決定する) と再帰呼び出し (問題を分割する) という 2 つの重要な要素で構成されます。より小さなサブ問題)。基本を理解し、階乗計算、フィボナッチ数列、バイナリ ツリー トラバーサルなどの実践的な例を練習することで、再帰的な直感を構築し、自信を持ってコードで使用することができます。




