確率行列
この記事の例では、ランダム行列について説明します。参考までに皆さんと共有してください。詳細は次のとおりです:
確率行列
私は過去に Google の並べ替えを検討していました。月 コア アルゴリズム ---PageRank ソート アルゴリズム [1][2]。これには、多くの論文 [3][4][5] でのグラフ理論とマルコフ連鎖の説明と応用が含まれます。私を常に困惑させてきた重要な文は、「A 確率行列には主/主固有値 1 があります」[3][4][5][6][7][8] です。おそらく、行列理論を体系的に勉強した人にとっては、それは非常に単純であり、個別に議論したり説明したりする価値はありません。そしてここで私は自分の無知を認めなければなりません。私は高度な代数における行列の性質についての議論をいくつか勉強したことがありますが、いわゆる確率行列 (Stochastic Matrix) については、ましてやその性質に触れたことはありませんでした。そこで、インターネット上で関連する文献を懸命に探しましたが、結果はあまり理想的とは言えず、ランダム行列や関連する性質の証明についての詳細な紹介はありませんでした。おそらく、私の検索技術がまだ成熟していないか、検索キーワードが不正確であるか、インターネット上にそれに関する情報が不足しているのだと思います。ここでは、私が最近収集した関連情報を取り出し、将来に活用するためのアイデアを整理したいと思いますが、これは私自身の学習の実際の記録と監修でもあります。
ランダム行列は、実際には非負行列の一種です (非負行列 )。非負行列とは、行列の要素がすべて非負であることを意味します (Nonnegative#) ##). もちろん、非負行列は正行列 (正行列 ) とわずかに区別する必要があります。非負の行列は、計算数学、グラフ理論、線形計画法、自動制御などの分野で広く使用されており、その固有値、特に最大固有値 (ここでの最大値はモジュールの観点または絶対値の概念からのものであることに注意してください) ) 最大) 固有値、つまり行列の主固有値 (主固有値/主固有値) の推定は非常に重要です [9]。
ランダム行列は非常に重要ですが、ランダム行列とはどのような行列ですか?非負の行列がランダムに与えられた場合、それがランダムな行列であるかどうかをどのように判断するのでしょうか? 確率行列は、実際には行確率行列 (行確率行列 ) と列確率行列 (列確率行列 ) に分割する必要があります。行ランダム行列は、行の合計が 1 に等しい正方行列であり、列ランダム行列は、列の合計が 1 に等しい非負の行列です。このとき、行と列の和が両方とも 1 を満たす非負の行列は二重確率行列 (Double 確率行列 ) であり、単位行列は二重確率行列です。研究の観点から見ると、実際には行行列の特性を研究するだけでよく、結局のところ、列ランダム行列は行ランダム行列の転置行列にすぎません。したがって、以下の説明は完全に行ランダム行列に基づいています。
ランダム行列 A の行合計が 1 であるため、e=(1,1,...,1) と仮定すると、e の転置ベクトル e' は行列の固有ベクトルであり、次のようになります。 A の固有値は 1 です。このように、ランダム行列の主固有値が 1 であることを証明するには、まだ一定の距離があります。 A の n 個の固有値が λ(i) (i=1,2,...,n) であると仮定します。この特性が真であることを証明したい場合は、 |λ(i)| そこで、関連する情報を探して「数学博士フォーラム」にアドバイスを求めるメッセージを投稿したところ、「それを証明してください。大まかに言うと、円板定理が使えます。」という返事が返ってきました。より正確に証明したい場合は、ペロン-フロベニウスの定理[9][10][11][12]を使用する必要があります。新しい概念や手法が次々と登場しており、数値手法や数値計算理論の体系的な検討が必要と思われます。見つかった情報 [10] は、任意の行列のスペクトル半径がその行列のどの誘導行列ノルムよりも大きくなく、ランダム行列の L1-Norm 値が 1 であることを示しています。スペクトル半径 (つまり、主固有値です) は 1 より大きくなく、1 は A の固有値であるため、絶対値が 1 より大きい固有値を持つことは不可能です。つまり、1 は確かに A の主固有値です。ランダム行列 A。
したがって、上記の性質の証明は、証明データ [10] の結論に相当します。 実際、「いかなる複素場における行列のスペクトル半径も、その誘導ノルムよりも大きくない」というのは、行列の基本的な性質にすぎません。具体的な証明を以下の図に示します。
ランダム行列の主固有値と 2 番目に大きい固有値 の比は、べき乗法の収束速度の基本的な尺度です。 PageRank を計算するには多くの方法があり、これに関する研究は数え切れないほどあります。もちろん、最も伝統的な方法は、べき乗法を使用して各 Web ページの PageRank 値を決定することです。データベースにクロールされました。 Web ページの数は膨大であるため、べき乗法の収束速度を考慮することは冗長で無駄な分析ではありません。 2 つの固有値の「スペクトル ギャップ」(Eigengap) は、主にべき乗法を使用して得られる PR 値の安定性を測定するために使用されます。この観点から、固有値分析は PageRank アルゴリズムを理解する上で重要な役割を果たします。
関連する推奨事項:
php バージョンのスパイラル マトリックス (内側から外側へ)
PHP は N*M 文字を実装しますマトリックスの 90 度回転
以上が確率行列の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7477
7477
 15
15
 1377
1377
 52
52
 77
77
 11
11
 19
19
 32
32
 Ubuntu および Debian 用の PHP 8.4 インストールおよびアップグレード ガイド
Dec 24, 2024 pm 04:42 PM
Ubuntu および Debian 用の PHP 8.4 インストールおよびアップグレード ガイド
Dec 24, 2024 pm 04:42 PM
PHP 8.4 では、いくつかの新機能、セキュリティの改善、パフォーマンスの改善が行われ、かなりの量の機能の非推奨と削除が行われています。 このガイドでは、Ubuntu、Debian、またはその派生版に PHP 8.4 をインストールする方法、または PHP 8.4 にアップグレードする方法について説明します。
 CakePHP について話し合う
Sep 10, 2024 pm 05:28 PM
CakePHP について話し合う
Sep 10, 2024 pm 05:28 PM
CakePHP は、PHP 用のオープンソース フレームワークです。これは、アプリケーションの開発、展開、保守をより簡単にすることを目的としています。 CakePHP は、強力かつ理解しやすい MVC のようなアーキテクチャに基づいています。モデル、ビュー、コントローラー
 CakePHP ファイルのアップロード
Sep 10, 2024 pm 05:27 PM
CakePHP ファイルのアップロード
Sep 10, 2024 pm 05:27 PM
ファイルのアップロードを行うには、フォーム ヘルパーを使用します。ここではファイルアップロードの例を示します。
 PHP 開発用に Visual Studio Code (VS Code) をセットアップする方法
Dec 20, 2024 am 11:31 AM
PHP 開発用に Visual Studio Code (VS Code) をセットアップする方法
Dec 20, 2024 am 11:31 AM
Visual Studio Code (VS Code とも呼ばれる) は、すべての主要なオペレーティング システムで利用できる無料のソース コード エディター (統合開発環境 (IDE)) です。 多くのプログラミング言語の拡張機能の大規模なコレクションを備えた VS Code は、
 CakePHP クイックガイド
Sep 10, 2024 pm 05:27 PM
CakePHP クイックガイド
Sep 10, 2024 pm 05:27 PM
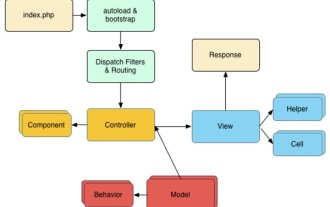
CakePHP はオープンソースの MVC フレームワークです。これにより、アプリケーションの開発、展開、保守がはるかに簡単になります。 CakePHP には、最も一般的なタスクの過負荷を軽減するためのライブラリが多数あります。
 PHPでHTML/XMLを解析および処理するにはどうすればよいですか?
Feb 07, 2025 am 11:57 AM
PHPでHTML/XMLを解析および処理するにはどうすればよいですか?
Feb 07, 2025 am 11:57 AM
このチュートリアルでは、PHPを使用してXMLドキュメントを効率的に処理する方法を示しています。 XML(拡張可能なマークアップ言語)は、人間の読みやすさとマシン解析の両方に合わせて設計された多用途のテキストベースのマークアップ言語です。一般的にデータストレージに使用されます