Pythonでニューラルネットワークモデルを作成する内容を簡単に理解しましょう-Python チュートリアル-php.cn

この記事では、Python でニューラルネットワークモデルを作成する方法を簡単に説明します。一定の参考値があります。必要な友人は参照できます。お役に立てば幸いです。

概要: ニューラルネットワークがどのように機能するかについて興味がありますか?ニューラルネットワークがどのように機能するかを理解する最良の方法は、単純なニューラルネットワークを自分で作成することです。

ニューラルネットワーク (NN) は、人工ニューラルネットワーク (ANN) とも呼ばれ、機械学習分野の学習アルゴリズムのサブセットであり、生物学的ニューラルネットワークの概念を大まかに借用しています。現在、ニューラルネットワークはコンピュータビジョンや自然言語処理などの分野で広く使われています。ドイツの機械学習上級専門家である Andrey Bulezyuk 氏は、「ニューラルネットワークは、人間の介入をほとんど必要とせずに、さまざまな分野や業界の複雑な抽象化を効果的にシミュレートできるため、機械学習に革命をもたらしています。」と述べています。次のコンポーネント:

データを送受信する入力層、
隠し層、
出力層;
#このチュートリアルでは、単純な Sigmoid 活性化関数が使用されますが、ディープニューラルネットワークモデルでは、勾配分散が発生しやすいため、Sigmoid 活性化関数は一般に第一選択ではないことに注意してください。

さらに、フィードフォワードニューラルネットワーク、畳み込みニューラルネットワーク、リカレントニューラルネットワークなど、いくつかの異なるタイプの人工ニューラルネットワークがあります。この記事では、単純なフィードフォワードニューラルネットワークまたは知覚ニューラルネットワークを例に挙げます。このタイプの人工ニューラルネットワークは、データを前から後ろに直接転送します。これは順伝播プロセスと呼ばれます。

フィードフォワードニューロンのトレーニングには通常、逆伝播アルゴリズムが必要です。これには、ネットワークに対応する入力セットと出力セットが必要です。入力データがニューロンに送信されると、それに応じて処理され、その結果の出力が次の層に送信されます。

次の図は、ニューラルネットワークの構造を簡単に示しています。

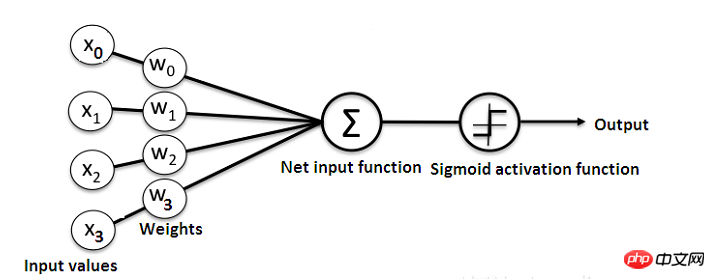Pythonでニューラルネットワークモデルを作成する内容を簡単に理解しましょうさらに、ニューラルネットワークがどのように機能するかを理解する最良の方法は、学習することです。ツールボックスを使用してゼロから構築する方法。この記事では、Python を使用して簡単なニューラルネットワークを作成する方法を説明します。

問題

下の表は、私たちが解決する問題を示しています:

新しいセットが与えられたときに正しい出力値を予測できるようにニューラルネットワークをトレーニングします。データ。

表からわかるように、出力値は常に入力セクションの最初の値と等しくなります。したがって、新しい状況の出力 (?) 値は 1 であることが期待できます。

Python コードを使用して同じ結果が得られるかどうかを見てみましょう。

ニューラルネットワーククラスの作成|NeuralNetwork クラス

正確な予測を提供するためにニューロンをトレーニングするために、Python で NeuralNetwork クラスを作成します。このクラスには、他の補助関数も含まれています。この単純なニューラルネットワークの例を作成するためにニューラルネットワークライブラリを使用しませんが、計算を支援するために基本的な Numpy ライブラリをインポートします。

Numpy ライブラリはデータ処理用の基本ライブラリであり、次の 4 つの重要な計算メソッドがあります:

EXP - 自然指数の生成に使用されます。

配列 — 行列の生成に使用されます;
ドット — 行列の乗算に使用されます;
random - 乱数の生成に使用されます;
シグモイド関数の適用

この関数は、0 から 1 までの任意の値をマッピングでき、入力の加重合計を正規化するのに役立ちます。 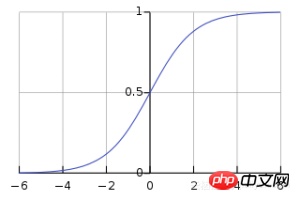Pythonでニューラルネットワークモデルを作成する内容を簡単に理解しましょうこの後、重みの基本的な調整を計算するためにシグモイド関数の導関数を作成します。

シグモイド関数の出力は、その導関数を生成するために使用できます。たとえば、出力変数が「x」の場合、その導関数は x *(1-x) になります。

モデルのトレーニング

モデルのトレーニングとは、ニューラルネットワークに正確な予測を行うよう教える段階を意味します。各入力には正または負の重みがあります。つまり、正の重みまたは負の重みが大きい入力は、結果の出力に大きな影響を与えます。

モデルが最初にトレーニングされるとき、各重みは乱数で初期化されることに注意してください。

次は、この記事で構築されたニューラルネットワークのサンプル問題のトレーニングプロセスです:

1. トレーニングデータセットから入力を取得し、その重みに従っていくつかの調整を行います。を介してニューラルネットワークを計算します。出力メソッドはレイヤーごとに送信するために使用されます;

2. バックプロパゲーションの誤り率を計算します。この場合、それはニューロンの予測出力とトレーニングデータセットの期待出力の間の誤差です;

3. 得られた誤差範囲に基づいて、重み付けされた誤差を使用します。導関数この式では、いくつかの小さな重み調整が行われます;

##4。このプロセスを 15,000 回繰り返し、各反復中にトレーニングセット全体が同時に処理されます。

##ここでは、「.T」関数を使用して行列にバイアスをかけます。したがって、数値は次のように保存されます。

Pythonでニューラルネットワークモデルを作成する内容を簡単に理解しましょう最終的に、ニューロンの重みは、提供されたトレーニングデータに合わせて最適化されます。したがって、ニューラルネットワークの出力が期待される出力と一致していれば、学習は完了し、正確な予測が可能であることを意味する、これがバックプロパゲーションの手法です。

カプセル化

最後に、NeuralNetwork クラスを初期化してプログラム全体を実行した後、Python プロジェクトでニューラルネットワークを作成する方法を示す完全なコードを以下に示します。

import numpy as np

class NeuralNetwork():
    
    def __init__(self):
        # 设置随机数种子
        np.random.seed(1)
        
        # 将权重转化为一个3x1的矩阵，其值分布为-1~1，并且均值为0
        self.synaptic_weights = 2 * np.random.random((3, 1)) - 1

    def sigmoid(self, x):
        # 应用sigmoid激活函数
        return 1 / (1 + np.exp(-x))

    def sigmoid_derivative(self, x):
        #计算Sigmoid函数的偏导数
        return x * (1 - x)

    def train(self, training_inputs, training_outputs, training_iterations):
        
        # 训练模型
        for iteration in range(training_iterations):
            # 得到输出
            output = self.think(training_inputs)

            # 计算误差
            error = training_outputs - output
            
            # 微调权重
            adjustments = np.dot(training_inputs.T, error * self.sigmoid_derivative(output))

            self.synaptic_weights += adjustments

    def think(self, inputs):
        # 输入通过网络得到输出   
        # 转化为浮点型数据类型
        
        inputs = inputs.astype(float)
        output = self.sigmoid(np.dot(inputs, self.synaptic_weights))
        return output


if __name__ == "__main__":

    # 初始化神经类
    neural_network = NeuralNetwork()

    print("Beginning Randomly Generated Weights: ")
    print(neural_network.synaptic_weights)

    #训练数据
    training_inputs = np.array([[0,0,1],
                                [1,1,1],
                                [1,0,1],
                                [0,1,1]])

    training_outputs = np.array([[0,1,1,0]]).T

    # 开始训练
    neural_network.train(training_inputs, training_outputs, 15000)

    print("Ending Weights After Training: ")
    print(neural_network.synaptic_weights)

    user_input_one = str(input("User Input One: "))
    user_input_two = str(input("User Input Two: "))
    user_input_three = str(input("User Input Three: "))
    
    print("Considering New Situation: ", user_input_one, user_input_two, user_input_three)
    print("New Output data: ")
    print(neural_network.think(np.array([user_input_one, user_input_two, user_input_three])))
    print("Wow, we did it!")

ログイン後にコピー

以下はコードを実行した後の出力結果です:

Pythonでニューラルネットワークモデルを作成する内容を簡単に理解しましょう # 上記は、作成できた単純なニューラルネットワークです。まず、ニューラルネットワークは自分自身にランダムな重みを割り当て始め、その後、トレーニングサンプルを使用して自分自身をトレーニングします。

したがって、新しいサンプル入力 [1,0,0] が表示された場合、その出力値は 0.9999584 になります。予想される正解は 1 であり、両者は非常に近いと言えますが、シグモイド関数が非線形関数であることを考慮すると、この誤差は許容されます。

さらに、この記事では、単純なタスクを実行するためにニューラルネットワークの 1 つの層のみを使用します。これらの人工ニューラルネットワークを何千も組み合わせたらどうなるでしょうか?人間の思考を100％真似できるでしょうか？答えは「はい」ですが、現時点では実装が難しく、非常に似ているとしか言えません。これに興味のある読者は、ディープラーニングに関連する資料を読むことができます。

以上がPythonでニューラルネットワークモデルを作成する内容を簡単に理解しましょうの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。